associated to the m th stimulus type with the canonical HRF 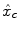 , i.e. a composition of two gamma functions which reflects the BOLD signal best in the visual and motor cortices [8]. The GLM therefore reads:
, i.e. a composition of two gamma functions which reflects the BOLD signal best in the visual and motor cortices [8]. The GLM therefore reads:
![$$\displaystyle{ \left [\boldsymbol{y}_{1},\,\ldots,\,\boldsymbol{y}_{J}\right ] = \mathbf{X}\left [\boldsymbol{a}\,_{1},\,\ldots,\,\boldsymbol{a}\,_{J}\right ] + \left [\mathbf{b}_{1},\,\ldots,\,\mathbf{b}_{J}\right ] }$$](/wp-content/uploads/2016/09/A151032_1_En_23_Chapter_Equ1.gif)
(1)
where 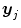 is the fMRI time series measured in voxel V j at times
is the fMRI time series measured in voxel V j at times 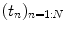 and
and 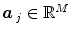 defines the vector of BOLD effects in V j for all stimulus type m = 1: M. Noise
defines the vector of BOLD effects in V j for all stimulus type m = 1: M. Noise 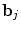 is usually modelled as a first-order autoregressive (i.e. AR(1)) process in order to account for the spatially-varying temporal correlation of fMRI data [5]:
is usually modelled as a first-order autoregressive (i.e. AR(1)) process in order to account for the spatially-varying temporal correlation of fMRI data [5]: 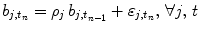 , with
, with 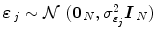 , where
, where 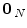 is a null vector of length N, and
is a null vector of length N, and 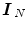 stands for the identity matrix of size N. Then, the estimated BOLD magnitudes
stands for the identity matrix of size N. Then, the estimated BOLD magnitudes 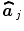 in V j are computed in the maximum likelihood sense by:
in V j are computed in the maximum likelihood sense by:
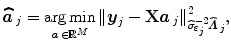
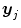 is the fMRI time series measured in voxel V j at times
is the fMRI time series measured in voxel V j at times  and
and 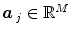 defines the vector of BOLD effects in V j for all stimulus type m = 1: M. Noise
defines the vector of BOLD effects in V j for all stimulus type m = 1: M. Noise 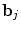 is usually modelled as a first-order autoregressive (i.e. AR(1)) process in order to account for the spatially-varying temporal correlation of fMRI data [5]:
is usually modelled as a first-order autoregressive (i.e. AR(1)) process in order to account for the spatially-varying temporal correlation of fMRI data [5]: 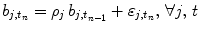 , with
, with 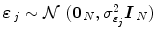 , where
, where 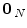 is a null vector of length N, and
is a null vector of length N, and 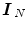 stands for the identity matrix of size N. Then, the estimated BOLD magnitudes
stands for the identity matrix of size N. Then, the estimated BOLD magnitudes 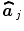 in V j are computed in the maximum likelihood sense by:
in V j are computed in the maximum likelihood sense by: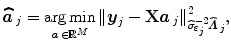
(2)
where 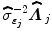 defines the inverse of the estimated autocorrelation matrix of
defines the inverse of the estimated autocorrelation matrix of 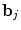 ; see for instance [9] for details about the identification of the noise structure. Later, extensions that incorporate prior information on the BOLD effects
; see for instance [9] for details about the identification of the noise structure. Later, extensions that incorporate prior information on the BOLD effects 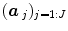 have been developed in the Bayesian framework [10]. In such cases, vectors
have been developed in the Bayesian framework [10]. In such cases, vectors 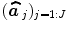 are computed using more computationally demanding strategies [10]. However, all these GLM-based contributions consider a unique and global model of the HRF shape while intra-individual differences in its characteristics have been exhibited between cortical areas [11].
are computed using more computationally demanding strategies [10]. However, all these GLM-based contributions consider a unique and global model of the HRF shape while intra-individual differences in its characteristics have been exhibited between cortical areas [11].
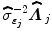 defines the inverse of the estimated autocorrelation matrix of
defines the inverse of the estimated autocorrelation matrix of 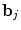 ; see for instance [9] for details about the identification of the noise structure. Later, extensions that incorporate prior information on the BOLD effects
; see for instance [9] for details about the identification of the noise structure. Later, extensions that incorporate prior information on the BOLD effects 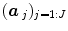 have been developed in the Bayesian framework [10]. In such cases, vectors
have been developed in the Bayesian framework [10]. In such cases, vectors 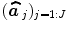 are computed using more computationally demanding strategies [10]. However, all these GLM-based contributions consider a unique and global model of the HRF shape while intra-individual differences in its characteristics have been exhibited between cortical areas [11].
are computed using more computationally demanding strategies [10]. However, all these GLM-based contributions consider a unique and global model of the HRF shape while intra-individual differences in its characteristics have been exhibited between cortical areas [11].2.2 Flexible GLM models
Intra-individual differences in the characteristics of the HRF have been exhibited between cortical areas in [11–14]. Although smaller than inter-individual fluctuations, this regional variability is large enough to be regarded with care. To account for these spatial fluctuations at the voxel level, one usually resorts to hemodynamic function basis. For instance, the canonical HRF 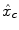 can be supplemented with its first and second time derivatives (
can be supplemented with its first and second time derivatives (![$$\left [\hat{x}_{c}\,\vert \,\hat{x}_{c}'\,\vert \,\hat{x}''_{c}\right ]$$](/wp-content/uploads/2016/09/A151032_1_En_23_Chapter_IEq17.gif) ) to model eg. differences in time-to-peak. Although powerful and elegant, flexibility is achievable at the expense of fewer effective degrees of freedom and decreased sensitivity in any subsequent statistical test. Importantly, in a GLM involving several regressors per condition, the BOLD effect becomes multivariate (i.e.
) to model eg. differences in time-to-peak. Although powerful and elegant, flexibility is achievable at the expense of fewer effective degrees of freedom and decreased sensitivity in any subsequent statistical test. Importantly, in a GLM involving several regressors per condition, the BOLD effect becomes multivariate (i.e. 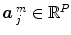 ) and the Student-t statistic can no longer be used to infer on differences
) and the Student-t statistic can no longer be used to infer on differences 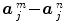 between the m th and n th stimulus types. Rather, an unsigned Fisher statistic has to be computed, making direct interpretation of activation maps more difficult. Indeed, the null hypothesis is actually rejected whenever any of the contrast components deviates from zero and not specifically when the difference of the response magnitudes is far from zero.
between the m th and n th stimulus types. Rather, an unsigned Fisher statistic has to be computed, making direct interpretation of activation maps more difficult. Indeed, the null hypothesis is actually rejected whenever any of the contrast components deviates from zero and not specifically when the difference of the response magnitudes is far from zero.
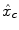 can be supplemented with its first and second time derivatives (
can be supplemented with its first and second time derivatives (![$$\left [\hat{x}_{c}\,\vert \,\hat{x}_{c}'\,\vert \,\hat{x}''_{c}\right ]$$](/wp-content/uploads/2016/09/A151032_1_En_23_Chapter_IEq17.gif) ) to model eg. differences in time-to-peak. Although powerful and elegant, flexibility is achievable at the expense of fewer effective degrees of freedom and decreased sensitivity in any subsequent statistical test. Importantly, in a GLM involving several regressors per condition, the BOLD effect becomes multivariate (i.e.
) to model eg. differences in time-to-peak. Although powerful and elegant, flexibility is achievable at the expense of fewer effective degrees of freedom and decreased sensitivity in any subsequent statistical test. Importantly, in a GLM involving several regressors per condition, the BOLD effect becomes multivariate (i.e. 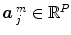 ) and the Student-t statistic can no longer be used to infer on differences
) and the Student-t statistic can no longer be used to infer on differences 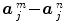 between the m th and n th stimulus types. Rather, an unsigned Fisher statistic has to be computed, making direct interpretation of activation maps more difficult. Indeed, the null hypothesis is actually rejected whenever any of the contrast components deviates from zero and not specifically when the difference of the response magnitudes is far from zero.
between the m th and n th stimulus types. Rather, an unsigned Fisher statistic has to be computed, making direct interpretation of activation maps more difficult. Indeed, the null hypothesis is actually rejected whenever any of the contrast components deviates from zero and not specifically when the difference of the response magnitudes is far from zero.2.3 Beyond parametric modelling
The localisation of brain activation strongly depends on the modelling of the brain response and thus of its estimation. Of course, the converse also holds: HRF estimation is only relevant in voxels that elicit signal fluctuations correlated with the paradigm. Hence, detection and estimation are intrinsically linked to each other. The key point is therefore to tackle the two problems in a common setting, i.e. to set up a formulation in which detection and estimation enter naturally and simultaneously. This setting cannot be the classical hypothesis testing framework. Indeed, the sequential procedure which consists in first estimating the HRF on a given dataset and then building a specific GLM upon this estimate for detecting activations in the same dataset, entails statistical problems in terms of sensitivity and specificity: the control of the false positive rate actually becomes hazardous due to the use of an erroneous number of degrees of freedom. Instead, we explore a Bayesian approach that provides an appropriate framework, called the Joint Detection Estimation (JDE) framework in what follows, to address both detection and estimation issues in the same formalism.
Regional non-parametric modelling of the BOLD signal
A spatially varying HRF model is necessary to keep a single regressor per condition, and thus enable direct statistical comparison (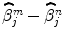 ). The JDE framework proposed in [15, 16] allows us to introduce such a spatially adaptive GLM in which a local estimation of
). The JDE framework proposed in [15, 16] allows us to introduce such a spatially adaptive GLM in which a local estimation of 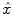 is performed. To conduct the analysis efficiently, HRF estimation is carried out at a regional scale coarser than the voxel level. To properly define this scale, the functional brain mask is divided in K functionally homogeneous parcels using the parcellation technique proposed in [17]. This algorithm relies on the minimisation of a compound criterion reflecting both the spatial and functional structures and hence the topology of the dataset. The spatial similarity measure favours the closeness in the Talairach coordinates system. The functional part of this criterion is computed on parameters that characterise the functional properties of the voxels, for instance the fMRI time series themselves.
is performed. To conduct the analysis efficiently, HRF estimation is carried out at a regional scale coarser than the voxel level. To properly define this scale, the functional brain mask is divided in K functionally homogeneous parcels using the parcellation technique proposed in [17]. This algorithm relies on the minimisation of a compound criterion reflecting both the spatial and functional structures and hence the topology of the dataset. The spatial similarity measure favours the closeness in the Talairach coordinates system. The functional part of this criterion is computed on parameters that characterise the functional properties of the voxels, for instance the fMRI time series themselves.
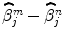 ). The JDE framework proposed in [15, 16] allows us to introduce such a spatially adaptive GLM in which a local estimation of
). The JDE framework proposed in [15, 16] allows us to introduce such a spatially adaptive GLM in which a local estimation of 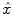 is performed. To conduct the analysis efficiently, HRF estimation is carried out at a regional scale coarser than the voxel level. To properly define this scale, the functional brain mask is divided in K functionally homogeneous parcels using the parcellation technique proposed in [17]. This algorithm relies on the minimisation of a compound criterion reflecting both the spatial and functional structures and hence the topology of the dataset. The spatial similarity measure favours the closeness in the Talairach coordinates system. The functional part of this criterion is computed on parameters that characterise the functional properties of the voxels, for instance the fMRI time series themselves.
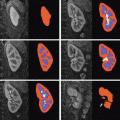
is performed. To conduct the analysis efficiently, HRF estimation is carried out at a regional scale coarser than the voxel level. To properly define this scale, the functional brain mask is divided in K functionally homogeneous parcels using the parcellation technique proposed in [17]. This algorithm relies on the minimisation of a compound criterion reflecting both the spatial and functional structures and hence the topology of the dataset. The spatial similarity measure favours the closeness in the Talairach coordinates system. The functional part of this criterion is computed on parameters that characterise the functional properties of the voxels, for instance the fMRI time series themselves.The number of parcels K is set by hand. The larger the number of parcels, the higher the degree of within-parcel homogeneity but potentially the lower the signal-to-noise ratio (SNR). To objectively choose an adequate number of parcels, Bayesian information criterion (BIC) and cross validation techniques have been used in [18] on an fMRI study of ten subjects. The authors have shown converging evidence for K ≈ 500 for a whole brain analysis leading to typical parcel sizes around a few hundreds voxels. Importantly, since the parcellation is derived at the group level, there is a one-to-one correspondance of parcels across subjects, as shown in Fig. 1.


Fig. 1
Sagittal views of a color-coded multi-subject parcellation. Left: Subject 1. Right: Subject 2
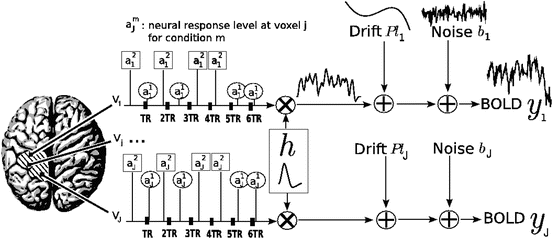
The parcel-based model of the BOLD signal introduced in [15, 16] is illustrated in Fig. 2. As shown, this model supposes that the HRF shape 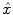 is constant within a parcel, while the magnitudes of activation a j m can vary in space and across stimulus types. Moreover, the model is said non-parametric since no model is assumed for the impulse response
is constant within a parcel, while the magnitudes of activation a j m can vary in space and across stimulus types. Moreover, the model is said non-parametric since no model is assumed for the impulse response 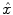 , which has therefore to be identified in each parcel. Let
, which has therefore to be identified in each parcel. Let 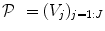 be the current parcel. Then, the generative BOLD model reads:
be the current parcel. Then, the generative BOLD model reads:
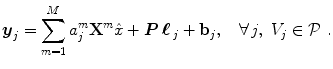
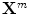 denotes the N × (D + 1) binary matrix that codes the onsets of the m th stimulus. Vector
denotes the N × (D + 1) binary matrix that codes the onsets of the m th stimulus. Vector 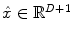 represents the unknown HRF shape in
represents the unknown HRF shape in 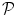 . The term
. The term 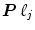 models a low-frequency trend to account for physiological artifacts and noise
models a low-frequency trend to account for physiological artifacts and noise 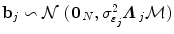 stands for the above mentioned AR(1) process.
stands for the above mentioned AR(1) process.
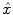 is constant within a parcel, while the magnitudes of activation a j m can vary in space and across stimulus types. Moreover, the model is said non-parametric since no model is assumed for the impulse response
is constant within a parcel, while the magnitudes of activation a j m can vary in space and across stimulus types. Moreover, the model is said non-parametric since no model is assumed for the impulse response 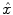 , which has therefore to be identified in each parcel. Let
, which has therefore to be identified in each parcel. Let 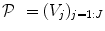 be the current parcel. Then, the generative BOLD model reads:
be the current parcel. Then, the generative BOLD model reads: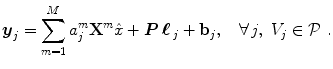
(3)
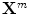 denotes the N × (D + 1) binary matrix that codes the onsets of the m th stimulus. Vector
denotes the N × (D + 1) binary matrix that codes the onsets of the m th stimulus. Vector 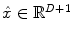 represents the unknown HRF shape in
represents the unknown HRF shape in 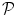 . The term
. The term 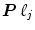 models a low-frequency trend to account for physiological artifacts and noise
models a low-frequency trend to account for physiological artifacts and noise 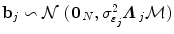 stands for the above mentioned AR(1) process.
stands for the above mentioned AR(1) process.
Fig. 2
Regional model of the BOLD signal in the JDE framework. The neural response levels a j m match with the BOLD effects a j m
Spatial mixture modelling and Bayesian inference
The HRF shape 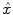 and the associated BOLD effects
and the associated BOLD effects 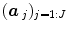 are jointly estimated in
are jointly estimated in 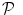 . Since no parametric model is considered for
. Since no parametric model is considered for 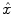 , a smoothness constraint on the second order derivative is introduced to regularise its estimation; see [15]. On the other hand, our approach also aims at detecting which voxels in
, a smoothness constraint on the second order derivative is introduced to regularise its estimation; see [15]. On the other hand, our approach also aims at detecting which voxels in 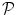 elicit activations in response to stimulation. To this end, prior mixture models are introduced on
elicit activations in response to stimulation. To this end, prior mixture models are introduced on 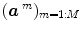 to segregate activating voxels from the non-activating ones in a stimulus-specific manner (i.e. for each m). In [16], it has been shown that Spatial Mixture Models (SMMs) make it possible to recover clusters of activation instead of isolated spots and hence to account for spatial correlation in the activation detection process without smoothing the data. As our approach stands in the Bayesian framework, other priors are formulated upon every other sought object in model (3). The reader is referred to [15, 16] for their expressions. Finally, inference is based upon the full posterior distribution
to segregate activating voxels from the non-activating ones in a stimulus-specific manner (i.e. for each m). In [16], it has been shown that Spatial Mixture Models (SMMs) make it possible to recover clusters of activation instead of isolated spots and hence to account for spatial correlation in the activation detection process without smoothing the data. As our approach stands in the Bayesian framework, other priors are formulated upon every other sought object in model (3). The reader is referred to [15, 16] for their expressions. Finally, inference is based upon the full posterior distribution 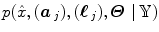 , which is sampled using a Gibbs sampling scheme [16]. Posterior mean (PM) estimates are therefore computed from these samples according to:
, which is sampled using a Gibbs sampling scheme [16]. Posterior mean (PM) estimates are therefore computed from these samples according to: 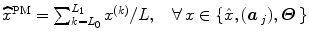 where
where 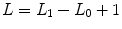 and L 0 stands for the length of the burn-in period. Note that this estimation process has to be repeated over each parcel of each subject’s brain. Since the fMRI data are considered spatially independent across parcels, parallel implementation makes the computation faster: whole brain analysis is achievable in about 60 mn for N = 125 and K = 500.
and L 0 stands for the length of the burn-in period. Note that this estimation process has to be repeated over each parcel of each subject’s brain. Since the fMRI data are considered spatially independent across parcels, parallel implementation makes the computation faster: whole brain analysis is achievable in about 60 mn for N = 125 and K = 500.
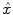 and the associated BOLD effects
and the associated BOLD effects 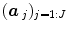 are jointly estimated in
are jointly estimated in 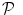 . Since no parametric model is considered for
. Since no parametric model is considered for 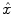 , a smoothness constraint on the second order derivative is introduced to regularise its estimation; see [15]. On the other hand, our approach also aims at detecting which voxels in
, a smoothness constraint on the second order derivative is introduced to regularise its estimation; see [15]. On the other hand, our approach also aims at detecting which voxels in 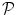 elicit activations in response to stimulation. To this end, prior mixture models are introduced on
elicit activations in response to stimulation. To this end, prior mixture models are introduced on 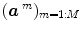 to segregate activating voxels from the non-activating ones in a stimulus-specific manner (i.e. for each m). In [16], it has been shown that Spatial Mixture Models (SMMs) make it possible to recover clusters of activation instead of isolated spots and hence to account for spatial correlation in the activation detection process without smoothing the data. As our approach stands in the Bayesian framework, other priors are formulated upon every other sought object in model (3). The reader is referred to [15, 16] for their expressions. Finally, inference is based upon the full posterior distribution
to segregate activating voxels from the non-activating ones in a stimulus-specific manner (i.e. for each m). In [16], it has been shown that Spatial Mixture Models (SMMs) make it possible to recover clusters of activation instead of isolated spots and hence to account for spatial correlation in the activation detection process without smoothing the data. As our approach stands in the Bayesian framework, other priors are formulated upon every other sought object in model (3). The reader is referred to [15, 16] for their expressions. Finally, inference is based upon the full posterior distribution 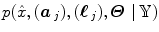 , which is sampled using a Gibbs sampling scheme [16]. Posterior mean (PM) estimates are therefore computed from these samples according to:
, which is sampled using a Gibbs sampling scheme [16]. Posterior mean (PM) estimates are therefore computed from these samples according to: 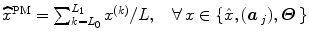 where
where 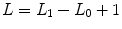 and L 0 stands for the length of the burn-in period. Note that this estimation process has to be repeated over each parcel of each subject’s brain. Since the fMRI data are considered spatially independent across parcels, parallel implementation makes the computation faster: whole brain analysis is achievable in about 60 mn for N = 125 and K = 500.
and L 0 stands for the length of the burn-in period. Note that this estimation process has to be repeated over each parcel of each subject’s brain. Since the fMRI data are considered spatially independent across parcels, parallel implementation makes the computation faster: whole brain analysis is achievable in about 60 mn for N = 125 and K = 500.2.4 Illustration on a real fMRI dataset
Data acquisition
Real fMRI data were recorded in fifteen volunteers during an experiment, which consisted of a single session of N = 125 scans lasting 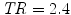 s each. The main goal of this experiment was to quickly map several brain functions such as motor, visual and auditory responses, as well as higher cognitive functions like computation. Here, we only focus on the auditory and visual experimental conditions and so on the auditory-visual contrast of interest (referenced as A. − V. ).
s each. The main goal of this experiment was to quickly map several brain functions such as motor, visual and auditory responses, as well as higher cognitive functions like computation. Here, we only focus on the auditory and visual experimental conditions and so on the auditory-visual contrast of interest (referenced as A. − V. ).
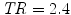 s each. The main goal of this experiment was to quickly map several brain functions such as motor, visual and auditory responses, as well as higher cognitive functions like computation. Here, we only focus on the auditory and visual experimental conditions and so on the auditory-visual contrast of interest (referenced as A. − V. ).
s each. The main goal of this experiment was to quickly map several brain functions such as motor, visual and auditory responses, as well as higher cognitive functions like computation. Here, we only focus on the auditory and visual experimental conditions and so on the auditory-visual contrast of interest (referenced as A. − V. ).Results
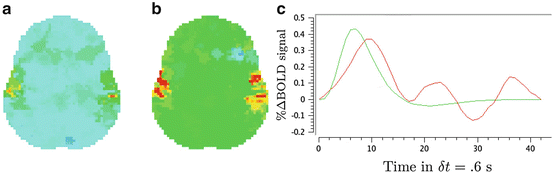
We compare the BOLD effect estimates for the two within-subject analyses under study. Fig. 3 clearly emphasizes for the A. − V. contrast that the JDE method achieves a better sensitivity (bilateral activations) in comparison with GLM-based inference when processing unsmoothed data. Indeed, the BOLD effects 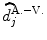 have higher values in Fig. 3(b) and appear more enhanced. This is partly due to the modeling of spatial correlation using SMM in the JDE framework. As shown in Fig. 3(c)-[red line], notice that the HRF estimate
have higher values in Fig. 3(b) and appear more enhanced. This is partly due to the modeling of spatial correlation using SMM in the JDE framework. As shown in Fig. 3(c)-[red line], notice that the HRF estimate 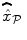 computed in the mostly activating parcel deviates from the canonical shape depicted in Fig. 3(c)[green line].
computed in the mostly activating parcel deviates from the canonical shape depicted in Fig. 3(c)[green line].
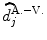 have higher values in Fig. 3(b) and appear more enhanced. This is partly due to the modeling of spatial correlation using SMM in the JDE framework. As shown in Fig. 3(c)-[red line], notice that the HRF estimate
have higher values in Fig. 3(b) and appear more enhanced. This is partly due to the modeling of spatial correlation using SMM in the JDE framework. As shown in Fig. 3(c)-[red line], notice that the HRF estimate 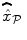 computed in the mostly activating parcel deviates from the canonical shape depicted in Fig. 3(c)[green line].
computed in the mostly activating parcel deviates from the canonical shape depicted in Fig. 3(c)[green line].