Fig. 1.
(a) The shape-based MIP approach with surface normals (arrows) interrogating the thin atrial wall imaged with LGE. (b) Contour from high resolution 3D whole heart b-SSFP scan superimposed on LGE to demonstrate mis-fitting in less common variants of LA anatomy (c) Atrial wall imaged in LGE scan and arrows showing areas where a manual annotation of epi- and endo-cardium is challenging.
In this work, we propose an image processing algorithm to segment the LA anatomy from a novel respiratory and cardiac ECG-gated magnetic resonance angiography (gated-MRA) sequence [1]. The gated-MRA scan provides for excellent atrial and venous anatomy. Unlike traditional MRA scans which are not cardiac-gated and acquired in breath-hold, they require registration to the LGE image sequence. With cardiac ECG-gating, both the gated-MRA and LGE images can be acquired in the same cardiac cycle, requiring no registration. With the proposed technique, the 3D reconstructions of fibrosis/scar and LA can be obtained with greater reliability than previous mentioned works.
2 Methods
2.1 Image Acquisition
All patients in this study (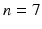 ) were scanned on a commercial 1.5T Ingenia MRI scanner (Philips Healthcare, The Netherlands). Electrocardiographic electrodes were positioned for optimal gating before the study. A free breathing, contrast enhanced MRA using an ECG triggered, respiratory gated, inversion recovery prepared, 3D image sequence was acquired. The acquisition was started 90 s after initiation of an intravenous infusion of Gadolinium (Gadovist, Bayer, Germany) at a rate of 0.3 ml/s. The reconstructed image pixel resolution was:
) were scanned on a commercial 1.5T Ingenia MRI scanner (Philips Healthcare, The Netherlands). Electrocardiographic electrodes were positioned for optimal gating before the study. A free breathing, contrast enhanced MRA using an ECG triggered, respiratory gated, inversion recovery prepared, 3D image sequence was acquired. The acquisition was started 90 s after initiation of an intravenous infusion of Gadolinium (Gadovist, Bayer, Germany) at a rate of 0.3 ml/s. The reconstructed image pixel resolution was: 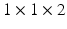 mm and typically 50 slices to cover the whole of the LA. A standard 3D LGE sequence was also performed using the same gating parameters. The reconstructed image pixel resolution was:
mm and typically 50 slices to cover the whole of the LA. A standard 3D LGE sequence was also performed using the same gating parameters. The reconstructed image pixel resolution was: 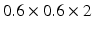 mm and 45–50 slices.
mm and 45–50 slices.
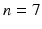 ) were scanned on a commercial 1.5T Ingenia MRI scanner (Philips Healthcare, The Netherlands). Electrocardiographic electrodes were positioned for optimal gating before the study. A free breathing, contrast enhanced MRA using an ECG triggered, respiratory gated, inversion recovery prepared, 3D image sequence was acquired. The acquisition was started 90 s after initiation of an intravenous infusion of Gadolinium (Gadovist, Bayer, Germany) at a rate of 0.3 ml/s. The reconstructed image pixel resolution was:
) were scanned on a commercial 1.5T Ingenia MRI scanner (Philips Healthcare, The Netherlands). Electrocardiographic electrodes were positioned for optimal gating before the study. A free breathing, contrast enhanced MRA using an ECG triggered, respiratory gated, inversion recovery prepared, 3D image sequence was acquired. The acquisition was started 90 s after initiation of an intravenous infusion of Gadolinium (Gadovist, Bayer, Germany) at a rate of 0.3 ml/s. The reconstructed image pixel resolution was: 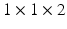 mm and typically 50 slices to cover the whole of the LA. A standard 3D LGE sequence was also performed using the same gating parameters. The reconstructed image pixel resolution was:
mm and typically 50 slices to cover the whole of the LA. A standard 3D LGE sequence was also performed using the same gating parameters. The reconstructed image pixel resolution was: 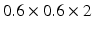 mm and 45–50 slices.
mm and 45–50 slices.
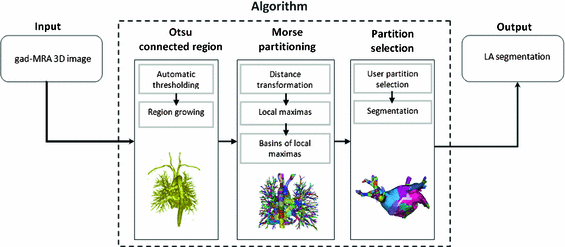
Fig. 2.
A flow diagram showing the steps in the proposed algorithm.
2.2 Algorithm
The steps involved in the proposed algorithm are shown as a flow diagram in Fig. 2. The algorithm exploits Morse partitions of the image. In Morse theory, the topology of sub-level sets of real-valued functions is connected to its critical points. In binary images, real-valued functions can be derived from the distance transformation, and the sub-level set consists of all voxels x where 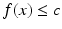 . The proposed algorithm partitions and thus segments the LA by exploiting the basins surrounding the local maxima of f(x). This is closely related to the watershed transform. In this work, the topology was defined by considering all voxels to be connected to its immediate neighbours (i.e. 26-neighbourhood or cubical complex). The algorithm was comprised of three steps: (1) Otsu region growing, (2) Morse partitioning, and (3) partition selection. Each step is herewith described in detail.
. The proposed algorithm partitions and thus segments the LA by exploiting the basins surrounding the local maxima of f(x). This is closely related to the watershed transform. In this work, the topology was defined by considering all voxels to be connected to its immediate neighbours (i.e. 26-neighbourhood or cubical complex). The algorithm was comprised of three steps: (1) Otsu region growing, (2) Morse partitioning, and (3) partition selection. Each step is herewith described in detail.
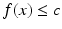 . The proposed algorithm partitions and thus segments the LA by exploiting the basins surrounding the local maxima of f(x). This is closely related to the watershed transform. In this work, the topology was defined by considering all voxels to be connected to its immediate neighbours (i.e. 26-neighbourhood or cubical complex). The algorithm was comprised of three steps: (1) Otsu region growing, (2) Morse partitioning, and (3) partition selection. Each step is herewith described in detail.
. The proposed algorithm partitions and thus segments the LA by exploiting the basins surrounding the local maxima of f(x). This is closely related to the watershed transform. In this work, the topology was defined by considering all voxels to be connected to its immediate neighbours (i.e. 26-neighbourhood or cubical complex). The algorithm was comprised of three steps: (1) Otsu region growing, (2) Morse partitioning, and (3) partition selection. Each step is herewith described in detail.In the Otsu region growing step, a connected region was obtained from a user-selected seed point and region of interest (ROI). The threshold in the Otsu step was computed on the gated-MRA image; it is the optimal intensity which partitions the image into two tissue classes. This was ideal in gated-MRA where there is a high contrast between blood and surrounding structures. The Otsu step generated a well-connected binary mask containing the LA and surrounding chambers.
In the Morse partitioning step illustrated in Fig. 3, the distance transform f(x) for the Otsu binary region was computed, where for every voxel x, f is the real-valued distance to the closest zero voxel. The local maxima of f was computed in an ensuing step. Basins surround each local maximum point in f. These basins are defined as voxels from which a path to the maxima exists. This path is the gradient flow  of f, where:
of f, where:
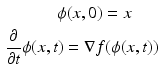 Each basin is a Morse partition B surrounding a critical point (i.e. local maximum) p:
Each basin is a Morse partition B surrounding a critical point (i.e. local maximum) p:
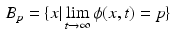 In the context of gated-MRA, the hollow LA chamber comprised of several local maxima on the distance transformation, yielding several such basins. The LA was generally connected to the aorta, coronaries and pulmonary artery due to partial voluming. Due to the nature of the distance transform and Morse partitions, rarely partitions spanned across chambers. For example, a partition spanning across the LA and aorta. It was this special feature of the algorithm that enabled the LA to be separated from its surrounding structures. However, a final partition selection step was necessary.
In the context of gated-MRA, the hollow LA chamber comprised of several local maxima on the distance transformation, yielding several such basins. The LA was generally connected to the aorta, coronaries and pulmonary artery due to partial voluming. Due to the nature of the distance transform and Morse partitions, rarely partitions spanned across chambers. For example, a partition spanning across the LA and aorta. It was this special feature of the algorithm that enabled the LA to be separated from its surrounding structures. However, a final partition selection step was necessary.
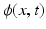 of f, where:
of f, where: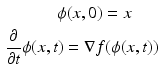
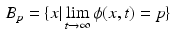
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree