the material coordinates of the undeformed cardiac domain  , by
, by 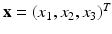 the spatial coordinates of the deformed cardiac domain
the spatial coordinates of the deformed cardiac domain 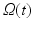 at time t, by
at time t, by 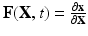 the deformation gradient. The cardiac tissue is modeled as a nonlinear hyperelastic material satisfying the steady-state force equilibrium equation
the deformation gradient. The cardiac tissue is modeled as a nonlinear hyperelastic material satisfying the steady-state force equilibrium equation
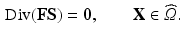
(1)
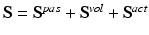 is the sum of passive, volumetric and active components. The passive and volumetric components are defined as
is the sum of passive, volumetric and active components. The passive and volumetric components are defined as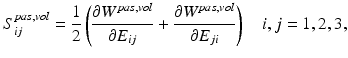
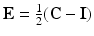 is the Green-Lagrange strain tensor,
is the Green-Lagrange strain tensor,  is an exponential strain energy function modeling the myocardium as an orthotropic hyperelastic material (see [14]), and
is an exponential strain energy function modeling the myocardium as an orthotropic hyperelastic material (see [14]), and 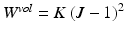 is a volume change penalization term, with K a positive bulk modulus and
is a volume change penalization term, with K a positive bulk modulus and 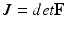 , added in order to model the myocardium as nearly incompressible.
, added in order to model the myocardium as nearly incompressible.(b) Mechanical Model of Active Tension. The active component 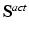 is given in terms of the active tension, that we assume developed along the myofiber direction only,
is given in terms of the active tension, that we assume developed along the myofiber direction only, 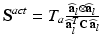 , with
, with 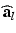 the fiber direction in the reference configuration and the biochemically generated active tension
the fiber direction in the reference configuration and the biochemically generated active tension 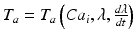 is calcium, stretch (
is calcium, stretch (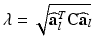 ), and stretch-rate (
), and stretch-rate (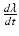 ) dependent, with the dynamics described by a system of ODEs proposed in Land et al. [21].
) dependent, with the dynamics described by a system of ODEs proposed in Land et al. [21].
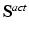 is given in terms of the active tension, that we assume developed along the myofiber direction only,
is given in terms of the active tension, that we assume developed along the myofiber direction only, 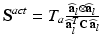 , with
, with 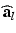 the fiber direction in the reference configuration and the biochemically generated active tension
the fiber direction in the reference configuration and the biochemically generated active tension 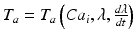 is calcium, stretch (
is calcium, stretch (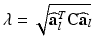 ), and stretch-rate (
), and stretch-rate (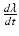 ) dependent, with the dynamics described by a system of ODEs proposed in Land et al. [21].
) dependent, with the dynamics described by a system of ODEs proposed in Land et al. [21].(c) Electrical Model of Cardiac Tissue: The Bidomain Model. We will use the following parabolic-elliptic formulation of the modified Bidomain model on the reference configuration 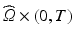 ,
,
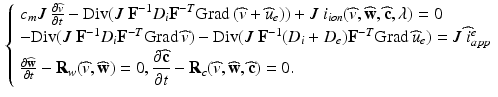
for the transmembrane potential 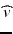 extracellular potential
extracellular potential 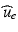 gating and ionic concentrations variables
gating and ionic concentrations variables 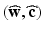 . This system is completed by prescribing initial conditions, insulating boundary conditions, and applied current
. This system is completed by prescribing initial conditions, insulating boundary conditions, and applied current 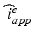 , see [11] for further details. The conductivity tensors are given by
, see [11] for further details. The conductivity tensors are given by
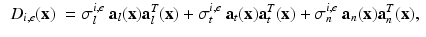
where 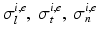 are the conductivity coefficients in the intra- and extracellular media measured along and across the fiber direction
are the conductivity coefficients in the intra- and extracellular media measured along and across the fiber direction 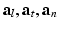 .
.
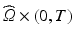 ,
,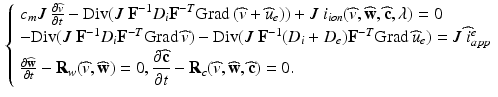
(2)
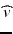 extracellular potential
extracellular potential 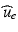 gating and ionic concentrations variables
gating and ionic concentrations variables 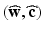 . This system is completed by prescribing initial conditions, insulating boundary conditions, and applied current
. This system is completed by prescribing initial conditions, insulating boundary conditions, and applied current 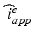 , see [11] for further details. The conductivity tensors are given by
, see [11] for further details. The conductivity tensors are given by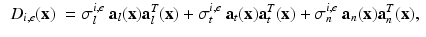
(3)
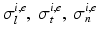 are the conductivity coefficients in the intra- and extracellular media measured along and across the fiber direction
are the conductivity coefficients in the intra- and extracellular media measured along and across the fiber direction 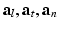 .
.(d) Ionic Membrane Model and Stretch-Activated Channel Current. The functions 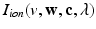 (
(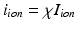 ),
), 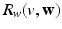 and
and 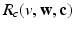 in the Bidomain model (2) are given by the ionic membrane model by ten Tusscher et al. [28], available from the cellML depository (models.cellml.org/cellml). The ionic current is the sum
in the Bidomain model (2) are given by the ionic membrane model by ten Tusscher et al. [28], available from the cellML depository (models.cellml.org/cellml). The ionic current is the sum 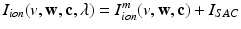 of the ionic term
of the ionic term 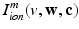 given by the ten Tusscher model and a stretch-activated channel current
given by the ten Tusscher model and a stretch-activated channel current 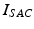 . This last current is modeled as in [22] as the sum of non-specific and specific currents
. This last current is modeled as in [22] as the sum of non-specific and specific currents 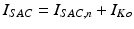 .
.
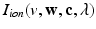 (
(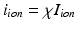 ),
), 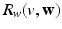 and
and 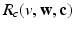 in the Bidomain model (2) are given by the ionic membrane model by ten Tusscher et al. [28], available from the cellML depository (models.cellml.org/cellml). The ionic current is the sum
in the Bidomain model (2) are given by the ionic membrane model by ten Tusscher et al. [28], available from the cellML depository (models.cellml.org/cellml). The ionic current is the sum 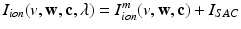 of the ionic term
of the ionic term 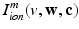 given by the ten Tusscher model and a stretch-activated channel current
given by the ten Tusscher model and a stretch-activated channel current 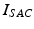 . This last current is modeled as in [22] as the sum of non-specific and specific currents
. This last current is modeled as in [22] as the sum of non-specific and specific currents 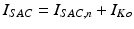 .
.3 Methods
Space Discretization. We discretize the cardiac domain with an hexahedral structured grid  for the mechanical model (1) and
for the mechanical model (1) and 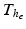 for the electrical Bidomain model (2), where
for the electrical Bidomain model (2), where 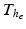 is a refinement of
is a refinement of 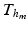 , i.e.
, i.e. 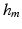 is an integer multiple of
is an integer multiple of 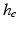 . We then discretize all scalar and vector fields of both mechanical and electrical models by isoparametric
. We then discretize all scalar and vector fields of both mechanical and electrical models by isoparametric 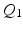 finite elements in space.
finite elements in space.
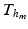 for the mechanical model (1) and
for the mechanical model (1) and 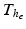 for the electrical Bidomain model (2), where
for the electrical Bidomain model (2), where 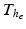 is a refinement of
is a refinement of 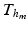 , i.e.
, i.e. 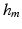 is an integer multiple of
is an integer multiple of 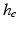 . We then discretize all scalar and vector fields of both mechanical and electrical models by isoparametric
. We then discretize all scalar and vector fields of both mechanical and electrical models by isoparametric 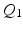 finite elements in space.
finite elements in space.Time Discretization. The time discretization is performed by a semi-implicit splitting method, where the electrical and mechanical time steps could be different. At each time step,
(a)
given 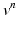 ,
, 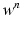 ,
, 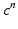 at time
at time 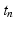 , solve the ODE system of the membrane model with a first order IMEX method to compute the new
, solve the ODE system of the membrane model with a first order IMEX method to compute the new 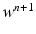 ,
, 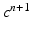 .
.
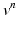 ,
, 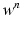 ,
, 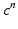 at time
at time 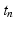 , solve the ODE system of the membrane model with a first order IMEX method to compute the new
, solve the ODE system of the membrane model with a first order IMEX method to compute the new 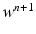 ,
, 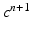 .
.(b)
given the calcium concentration 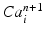 , which is included in the concentration variables
, which is included in the concentration variables 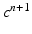 , solve the mechanical problems (1) and the active tension system to compute the new deformed coordinates
, solve the mechanical problems (1) and the active tension system to compute the new deformed coordinates 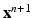 , providing the new deformation gradient tensor
, providing the new deformation gradient tensor 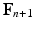 .
.
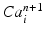 , which is included in the concentration variables
, which is included in the concentration variables 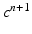 , solve the mechanical problems (1) and the active tension system to compute the new deformed coordinates
, solve the mechanical problems (1) and the active tension system to compute the new deformed coordinates 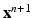 , providing the new deformation gradient tensor
, providing the new deformation gradient tensor 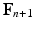 .
.(c)
given 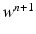 ,
, 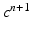 ,
, 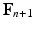 and
and 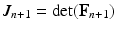 , solve the Bidomain system (2) with a first order IMEX method and compute the new electric potentials
, solve the Bidomain system (2) with a first order IMEX method and compute the new electric potentials 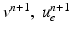 with an operator splitting method.
with an operator splitting method.
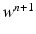 ,
, 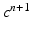 ,
, 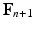 and
and 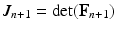 , solve the Bidomain system (2) with a first order IMEX method and compute the new electric potentials
, solve the Bidomain system (2) with a first order IMEX method and compute the new electric potentials 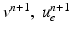 with an operator splitting method.
with an operator splitting method.We refer to [9] for more details.
Computational Kernels. Due to the employed space and time discretization strategies, at each time step, the main computational efforts consist of:
Domain Geometry and Parameter Calibration. The cardiac domain 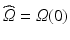 is the image of a cartesian slab using ellipsoidal coordinates, yielding a portion of truncated ellipsoid. The values of the orthotropic conductivity coefficients (see (3)) used in all the numerical tests are
is the image of a cartesian slab using ellipsoidal coordinates, yielding a portion of truncated ellipsoid. The values of the orthotropic conductivity coefficients (see (3)) used in all the numerical tests are 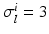 ,
, 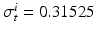 ,
, 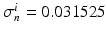 ,
, 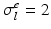 ,
, 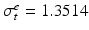 ,
, 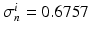 , all expressed in
, all expressed in 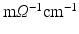 . The parameters of the orthotropic strain energy function are given in [14]. The bulk modulus is
. The parameters of the orthotropic strain energy function are given in [14]. The bulk modulus is 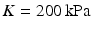 .
.
(i)
solving the nonlinear system deriving from the discretization of the mechanical problem by a Newton-GMRES-Algebraic Multigrid method, see [10];
(ii)
solving the two linear systems associated with the elliptic and parabolic Bidomain equations using the Conjugate Gradient method preconditioned by a Multilevel Additive Schwarz preconditioner studied in [23]. Our parallel simulations have been performed on a Linux cluster using the parallel library PETSc [6] from the Argonne National Laboratory.
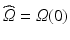 is the image of a cartesian slab using ellipsoidal coordinates, yielding a portion of truncated ellipsoid. The values of the orthotropic conductivity coefficients (see (3)) used in all the numerical tests are
is the image of a cartesian slab using ellipsoidal coordinates, yielding a portion of truncated ellipsoid. The values of the orthotropic conductivity coefficients (see (3)) used in all the numerical tests are 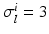 ,
, 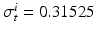 ,
, 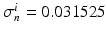 ,
, 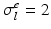 ,
, 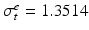 ,
, 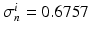 , all expressed in
, all expressed in 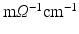 . The parameters of the orthotropic strain energy function are given in [14]. The bulk modulus is
. The parameters of the orthotropic strain energy function are given in [14]. The bulk modulus is 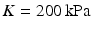 .
.