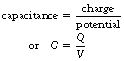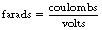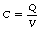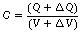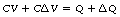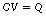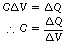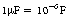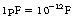Chapter 13 Capacitors

13.1 Aim

The aim of this chapter is to introduce the subject of capacitors and capacitance. It then considers the factors that influence the performance of a capacitor, how capacitors can be linked to other components and how capacitors are used in radiography.

13.2 Introduction

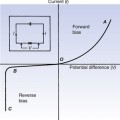
In Chapter 11, we considered the influence of a capacitor on the current and voltage in an alternating current (AC) circuit. We were able to do this without an understanding of the construction or the operation of a capacitor. There are circumstances where capacitors are used and where we need to understand either the construction and/or the operation of the capacitor to understand its function within the piece of equipment. This chapter deals with the physics of the capacitor, which is a device for storing electrical charge. It has many applications in radiography as it can be charged and discharged quickly unlike a battery.

13.3 Electrical capacity (capacitance)

We have previously shown in Chapter 6 that when a body has a net positive or negative charge it also possesses an electrical potential, because work must be done in moving a unit positive charge from infinity to the body. This potential is positive if the charge on the body is positive and negative if the charge on the body is negative.

The electrical capacity or capacitance of the body is the relationship between the charge put on the body and its potential:

Equation 13.1

13.3.1 Definitions and unit of capacitance (farad)

The definition of capacitance varies slightly depending on the type of body holding the charge. When a body consists of one surface only (e.g. a sphere) the following definition applies:

Definition

The capacitance of a body is the ratio of the total charge on the body to its potential.

If the body consists of two surfaces close together, we must consider the potential differences between the surfaces rather than the potential on each. This leads to the following alternative definition of capacitance:

Definition

The capacitance of a body is the ratio of the total charge of one sign on the body to the potential difference between its surfaces.

It is important to remember that capacitance involves both charge and potential and so it is not correct to think of capacitance as the ‘amount of charge a body can hold’ unless we add the phrase ‘per unit potential difference’. The International System of Units (SI) unit of capacitance is the farad and may be defined as:

Definition

An electrical system has a capacitance of 1 farad if a charge of 1 coulomb held by the body results in a potential (or potential difference) of 1 volt.

Thus, Equation 13.1 may be expressed as:

Equation 13.2

Definition

An alternative definition of capacitance, and one that is often more useful in radiography, is to consider capacitance in terms of the change of charge divided by the corresponding change in potential.

If a capacitor starts with a charge Q and a potential difference, then by definition:

Equation 13.2A

If an extra charge, ΔQ is added to the plates and an extra potential difference ΔV, results, then:

i.e. capacitance is the total charge divided by the total potential difference.

By cross-multiplying the above equation, we get:

Equation 13.2B

However, we can say from Equation A that:

Thus, Equation B can be rewritten:

This gives the alternative definition of capacitance, which can be used in radiography for calculations involving capacitor discharge circuits, etc.

For practical purposes, the farad (F) is rather a large unit in which to measure capacitance and so it is more commonly expressed in units of microfarads (μF) or picofarads (pF), where:

and

13.4 Capacitance of a parallel-plate capacitor

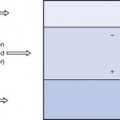
Figure 13.1 (see page 79) shows a parallel-plate capacitor with two plates of equal area, separated by a distance, d. The plates are made of electrical conductors so that charge may flow in and out of each plate. If the capacitor is charged– e.g. by connecting it across a battery as shown – then a charge of +Q will exist on one plate and a charge of −Q on the other. If the battery is disconnected, the charge will continue to be stored on the plates of the capacitor as the positive charge on one plate attracts the negative charge on the other. This is why a capacitor is often described as a device for storing charge. (A large capacitor will retain this charge for a long period of time after it has been disconnected from the source of electromotive force (EMF). For this reason, it should be treated with extreme care as severe electric shock may result from touching the plates or the electrical connections to the capacitor.)