I was a resident in radiology at the University of California, San Francisco (UCSF) during the early days of the development of x-ray computed tomography (CT). Prior to going to medical school, I had received a PhD in astrophysics from Princeton University. Thus, I was interested in both the technical aspects of this new imaging modality and its potential for new research and clinical applications. The first CT system I worked with at UCSF was one of the first models of the primitive EMI Mark 1 scanners, which took minutes to acquire the data for each (low resolution) image, using a time-consuming “translate-rotate” method of moving the x-ray tube and detector around the body. Thus, contrast enhancement was used only for static delineation of areas of altered late enhancement, such as that resulting from blood–brain barrier abnormalities. However, other data acquisition approaches were soon developed to speed up the imaging process. In particular, General Electric was exploring an approach to data acquisition that used only a rotating gantry incorporating an x-ray source and a detector array; a prototype CT system based on this was installed at UCSF while it was still in development. This new system enabled serial images to be acquired every few seconds, opening up the possibility of dynamically observing the process of contrast enhancement after administration of a bolus of contrast agent. When doing such dynamic imaging of the contrast enhancement after a bolus administration of contrast agent, a distinct sequence was clearly seen: first, the arrival of the contrast agent in arteries, then a “blush” of the tissue, followed by the appearance of the contrast agent in the draining veins. In subsequent images, further development of the tissue enhancement pattern could be observed, along with such phenomena as the appearance of a delayed recirculation of the contrast bolus (now diminished and prolonged). This suggested that it might be possible to use this dynamic information to assess the local delivery of blood to the tissue and its exchange and transit through it. As noninvasive assessment of perfusion had long been considered one of the “holy grails” of imaging, this was an exciting prospect.

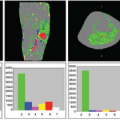
Although these pictures were interesting to look at, the next question that arose was how to analyze these dynamic imaging data. The traditional radiologic method for interpretation of images has been to use a “pattern recognition” approach, relying on a visual assessment of the images to identify and characterize areas of abnormality. This can be supplemented with simple quantitative analyses of things such as the relative brightness of different areas and the measurement of corresponding phenomenologic variables. Thus, the early approaches to the analysis of the dynamic CT enhancement patterns, by people like Burton Drayer, focused on qualitative descriptions of the patterns observed and on the measurement of variables such as the time until appearance of the contrast bolus in the arteries and the tissue, the time to the subsequent peak enhancement, and the area under the curve of enhancement versus time. Although these variables were interesting and they could be empirically correlated with other clinical information to better ascertain their significance, they did not provide a direct quantitative measurement of perfusion and related physiologic properties. With my training in astronomy, I was already conditioned to think of images as spatially distributed data, rather than just patterns to be qualitatively classified, and to use mathematical models of underlying mechanisms as a means to interpret imaged phenomena. Thus, I was dissatisfied with the conventional simple approach to the interpretation of dynamic CT images and sought to develop a more physiologically and quantitatively based approach.

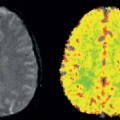
It was clear that the time course of the tissue attenuation during the passage of the contrast bolus would depend both on the intrinsic properties of the tissue microcirculation and on the amount and time course of the contrast agent delivered to it through the arteries. If the imaging process were linear (i.e., imaged attenuation changes were directly proportional to corresponding changes in contrast agent concentration, and the changes in tissue response to contrast agent were directly proportional to the input to it), and if I were able to get a reliable estimate of the arterial input function (AIF), I should be able to separate the two effects by performing some sort of deconvolution of the AIF from the tissue enhancement. Thus, I could effectively find the response that would be expected for a hypothetical instantaneous bolus input to the tissue. This “impulse response” should, in turn, be analyzable to find the corresponding underlying relevant
physiologic properties of the tissue. In reading about related analyses that had been used in pharmacokinetic modeling, and, in particular, analyses that had been made of the time course of the passage of radioactive tracers through the brain, as observed with external detectors over the head or by positron emission tomography imaging, I found that there was an existing body of “indicator-dilution” theory of the time course of tracers in tissues, which had been developed by people like K. Zierler and J. B. Bassingthwaighte, that should be directly applicable to the analysis of dynamic CT enhancement data. Some relevant elements of this theory included: (a) the characterization of the mean transit time (MTT) of an instantaneous bolus of tracer through the tissue, which depends on the ratio of the effective volume of distribution of the tracer in the tissue to the blood flow through the tissue; (b) the characterization of the fractional blood volume of the tissue as a parameter; (c) the classification of the behavior of the tracer during its transit through the tissue as being freely diffusible outside the vessels, confined to the intravascular space or somewhere in between; and (d) the characterization of the exchange of the tracer with the extravascular space through the permeability-surface area product. For a tracer such as a conventional radiographic contrast agent, which is excluded from the interior of intact cells and does not bind to any tissue components, the relevant blood volume is really the plasma volume, and the tissue distribution volume is the sum of the plasma volume and the extracellular-extravascular space. For the special case of a brain with an intact blood–brain barrier, the possibility of extravascular exchange of the tracer can be ignored and the MTT then simplifies to the ratio of the tissue plasma volume to the tissue plasma flow. Thus, if there is an independent estimate of the tissue blood volume and the relative hematocrit (not actually the same in the microcirculation and the large vessels), the blood flow (perfusion) through the brain from the MTT can be calculated.