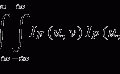Computer-Assisted Treatment Planning Approaches for Carbon-Ion Beam Therapy

Fig. 7.1

Dose distribution with passive scattering carbon-ion radiotherapy (CIRT) (upper panel) and IMRT (lower panel). Yellow arrows show beam fields (With permission from Tsujii et al. 2014)

In this chapter, we introduce basic concepts of carbon-ion beam treatment planning with image guidance/image processing (in a sense, image-guided particle therapy, IGPT) and emphasize the differences between particle beam therapy and photon beam therapy. Several recent articles on particle beam therapy provide important additional skill-building information (Jakel et al. 2008; Tsujii and Kamada 2012; Chen et al. 2009, 2006).

7.2 Why Choose Carbon Ions?

It is well known that the high energy of a therapeutic photon beam decreases in a steep exponential curve with penetration depth and that the dose close to the entrance surface shows “buildup” caused by forward-scattered Compton electrons. In contrast, charged particle beams provide superior dose conformation to photon beams and minimize excessive dose to normal tissues. These strengths owe to the characteristic increase in energy deposition of particle beams with penetration depth (proton and carbon-ion beams) up to a sharp maximum at the end of the beam range (Bragg peak) (Fig. 7.2) (Bragg and Kleeman 1904). Explained simply, accelerated particle beam interactions lose kinetic energy along the ray line due to the interaction of Coulomb forces with the target electrons (stopping power). This is expressed by the Bethe-Bloch formula. Stopping power is approximately proportional to (Z/v)²:

$\frac{\mathrm{d} E}{\mathrm{d} x}\sim \frac{Kn{\mathrm{Z}}^2}{v^2}\ \left[ \ln \left(\frac{2{m}_e{v}^2}{I}\right)\right]\propto {\left(\frac{\mathrm{Z}}{v}\right)}^2,$

(7.1)

where K, n, and m _eare the constant, electron density of the target material, and mass of electrons, respectively. Z is the charge of the projectile particle, v is the projectile velocity, and I is the mean ionization energy of the target atoms.

Fig. 7.2

Depth absorbed dose distributions of (a) a primary proton beam and its secondary particles and (b) a carbon-ion beam and its secondary particles (Reproduced from Kempe et al. 2007)

Accordingly, projectile velocity slows down as material penetration deepens, and stopping power is increased. Projectile velocity at the end of range is close to zero, and a high dose is deposited there.

In 1975–1992, neon ions and helium ions were used to treat 433 cancer patients and 2054 patients, respectively, at the Lawrence Berkeley National Laboratory (Alonso 2000), while in 1994, the heavy ion medical accelerator (HIMAC) at the National Institute of Radiological Sciences (NIRS) began providing carbon-ion radiotherapy (CIRT). From clinical experience gained at Berkeley, most heavy charged particle beam centers have selected carbon ions, mainly for the following reasons:

1.

Ions heavier than carbon have an increased nuclear fragmentation tail dose.

Protons did not deposit dose beyond the Bragg peak (Fig. 7.2a). In contrast, ions heavier than protons still had low projectile energy nuclear interactions (elastic collisions with target nuclei), providing a small dose (fragment particles with lower atomic number) beyond the Bragg peak (Fig. 7.2b).

2.

Ions heavier than carbon increase LET and relative biological effectiveness (RBE).

Conceptually, RBE represents the particle beam dose which provides the same biological effect as would be provided by the reference dose (typically X-rays or γ-rays). The RBE of light ions (proton, helium, etc.) does not significantly change between the entrance region and distal spread-out Bragg peak (SOBP) (Fig. 7.3). In contrast, the RBE of carbon ions is similar to that of light ions at the proximal SOBP but increased at the distal SOBP. The light-ion relative biological dose at the plateau region is therefore higher than the carbon-ion relative biological dose (Fig. 7.4). In contrast, the RBE of heavier ions (neon, argon, etc.) at the proximal and distal SOBPs is higher than that of carbon ions (although the RBE of neon at the entrance region is smaller than that of carbon ions at the distal SOBP). Although the relative biological dose of heavier ions at the SOBP is the same as that of carbon ions, the relative biological dose at the entrance region and proximal and distal SOBPs is higher than that of carbon ions. As a result, the peak to plateau ratio for carbon ions is higher and therefore improved, over that of other particle beams, including protons.

Fig. 7.3

Relative biological effectiveness (RBE) of different ions in fractionated irradiation of jejunal crypt cells of mice (With permission from Jakel 2009)

Fig. 7.4

Relative biological dose of the SOBP of ion beams. Doses are normalized at the SOBP region (With permission by the IAEA 2007)

3.

Heavier ions minimize the magnitude of range straggling and lateral scattering.

These factors blur out the sharp ionization peak. Range straggling causes smearing out of the depth of penetration of the stopping particle beam due to statistical fluctuations in the ionization process. The variance of the range straggling is expressed from Bohr’s theory as follows:

$\varphi (x)=\frac{1}{\sigma_x\sqrt{2\pi}} \exp \left(\frac{-{\left( x- R(E)\right)}^2}{2{\sigma}_x^2}\right),$

(7.2)

$R(E)={\int}_0^E{\left(\frac{\mathrm{d} E\prime }{\mathrm{d} x}\right)}^{-1}\mathrm{d} E^{\prime },$

(7.3)

where x is the penetration depth, σ _xis almost proportional to range R and inverse to the square root of the particle mass, and range straggling for helium and neon are about 50 and 20 % of that for protons, respectively. Lateral scattering is mainly caused by elastic Coulomb interactions with the target nuclei and can be approximated by Gaussian functions as follows (Highland 1975):

${\sigma}_{\theta}=\frac{14.1\mathrm{MeV}}{\beta pc}{Z}_p\sqrt{\frac{d}{L}}\left[1+\frac{1}{9}{ \log}_{10}\left(\frac{d}{L}\right)\right],$

(7.4)

where L and d are the radiation length and penetration length, respectively, β is particle beam velocity, and p and c are the momentum of the incident particle and the speed of light, respectively. The magnitude of the lateral scattering of photons and protons is larger than that for carbon ions at the same depth (Fig. 7.5).

Fig. 7.5

Lateral scattering of photon, proton, and carbon-ion beams as a function of penetration depth (With permission from Kraft 2000)

4.

Heavier ions require a large accelerator.

Due to differences in their mass-to-charge ratio, it is two times more difficult to bend a carbon-ion beam with an accelerator than protons under same magnetic field, and the range of carbon ions is three time shorter than that of protons under the same velocity. Carbon-ion beams therefore require higher energy than protons to obtain the same range by enlarging accelerator size. Current particle beam center construction costs are dominated by size of the accelerator, which requires a large housing size. Progress in accelerator technology over the last 20 years has contributed to cost reductions by reducing accelerator size. For example, the cost of the synchrotron ring at Gunma University, which was constructed in 2009, was 63 m, approximately half that of the NIRS, constructed in 1993.

Given the above, it appears that carbon ions represent a well-balanced particle in both physical and biological aspects (Table 7.1). In 2015, more than ten treatment centers were operating CIRT, as shown on the website of the PTCOG. The NIRS has treated over 8000 patients using carbon ions, and their clinical experience is reported here (Tsujii and Kamada 2012).

Table 7.1

Summary of the characteristics of particle beams

	Biological dose distribution	Range straggling and lateral scattering	Construction cost
Proton	Good	Poor	Excellent
Carbon ion	Excellent	Good	Good
Neon	Good	Excellent	Poor

7.3 Particle Beam Treatment Planning

7.3.1 Planning CT

CT imaging provides both patient 3D anatomical information and effective density information, making it an essential part of treatment planning. This 3D information is markedly helpful in deciding treatment parameters, especially beam angle and dose distribution. An immobilization device is typically used in the planning CT acquisition and treatment stages to improve patient positional reproducibility throughout the treatment course. Several treatment centers have installed a large bore CT (over 80 cm diameter) to avoid the conflict between positioning of the raised arm and immobilization which occurs with a standard bore CT (about 72 cm diameter).

Recent commercial CT scanners are equipped with a 4D mode to capture respiratory-induced organ motion. 4DCT is a breakthrough technique which allows the quantification of intrafractional uncertainties. This technique is applied in cardiac CT imaging and has already become practical for identifying patients with significant coronary artery stenosis by ECG-correlated preprocessing. Given the heartbeat (~ 1 s) is faster than respiratory motion (~ 4 s) and coronary arteries (~ a few mm) are smaller than lung tumors (~ a few cm), it should therefore be feasible to visualize intrafractional motion. Although the respiratory pattern shows variations (e.g., phase shift/drift), 4DCT scans provide information of a single exemplary respiratory cycle only. Thus, serial CT/4DCT image acquisition is performed over a certain time axis (daily, weekly, etc.) to obtain potential anatomical changes. This information can be helpful in considering replanning during the treatment course.

In photon beam therapy, megavoltage X-ray interaction in material is dominated by Compton scattering, and effective density is calibrated using relative electron density. Typically, HU (Hounsfield unit) values within the patient are measured by the planning CT image and converted to linear attenuation coefficients (μ):

$\mu =\left( HU-{HU}_{\mathrm{air}}\right){\left({HU_{\mathrm{water}}- HU}_{\mathrm{air}}\right)}^{-1},$

(7.5)

The linear attenuation coefficient is derived from the formula or photon attenuation (Rutherford et al. 1976):

$\mu ={\rho}_e\left({K}^{\mathrm{ph}}{Z}^{3.62}+{K}^{\mathrm{coh}}{Z}^{1.86}+{K}^{\mathrm{KN}}\right),$

(7.6)

where K ^ph, K ^coh, and K ^KN are constants for the contribution of the photoelectric effect, coherent scattering, and Compton scattering, respectively.

Particle beam ranges in materials are scaled by the stopping-power ratio relative to water based on measurement in water during beam commissioning. Accordingly, effective density in charged particle beams should be defined as the stopping power relative to water (ρ _s):

${\rho}_s={\rho}_e\left[ \ln \left(\frac{2{m}_e{c}^2}{I_{\mathrm{material}}}\frac{\beta^2}{1-{\beta}^2}\right)-{\beta}^2\right]{\left[ \ln \left(\frac{2{m}_e{c}^2}{I_{\mathrm{water}}}\frac{\beta^2}{1-{\beta}^2}\right)-{\beta}^2\right]}^{-1},$

(7.7)

where ρ _eand m _eare relative electron density and the electron mass, respectively, and I _material and I _water are the mean ionization energies in material and water, respectively. Several carbon-ion beam treatment centers in Japan use CT calibration using the polybinary tissue model (muscle (water), air, fat (ethanol), and bone (40 % K₂HPO₄ water)) due to the good balance it provides between quality and cost (Kanematsu et al. 2003). By doing this, dose distribution can be calculated by converting all CT image sets to the effective density in the treatment planning system (TPS).

7.3.2 Contouring

7.3.2.1 Volume of Interest (VOI)

Since the planning CT image contains patient anatomical information that the TPS does not recognize, the volume of interest (VOI) on the CT image should be input into the TPS to conform the prescribed dose to the tumor and to minimize dose to normal tissues. The International Commission on Radiation Units and Measurement (ICRU) first defined the VOI in ICRU report 50 (1993) and refined it further in ICRU reports 62 (1999), 71 (2005), and 78 (2007). These VOI terms are illustrated in Fig. 7.6, in which the target-related terms are gross tumor volume (GTV), clinical target volume (CTV), internal target volume (ITV), and planning target volume (PTV). The term “target volume” is often used for both target and healthy tissues but is more specific to the tumor. We therefore use VOI here to describe both tumor and normal tissues. Although the VOI is fully defined in these ICRU reports, I introduce it briefly here as follows.

Fig. 7.6

Schematic drawing of the volumes of interest relating to the definition of target and organs at risk

The GTV consists of a primary/metastatic tumor and demonstrable visible tumor region on planning images. It is generally delineated by the oncologist and may not be present following irradiation treatment. The CTV contains the GTV and subclinical malignant disease region (microscopic tumor spread region), which in some cases is difficult to observe in the planning CT image. To compensate for expected internal uncertainties such as physiologic movement and temporal size/shape/positional variations, the ITV is defined by adding an internal margin to the CTV. This internal margin technique is often used in thoracoabdominal treatment. The PTV is designed by adding a setup margin to the ITV. This setup margin accounts for the inaccuracy and low reproducibility of patient positioning to the treatment beam. The PTV in photon beam therapy generally uses the geometrical-based margins of the beam field to compensate for organ motion and setup errors. Since particle beam therapy considers uncertainties in beam penetration, the PTV should include the range-based proximal and distal margins of the beam field as well as the lateral margins. The PTV is therefore designed for each beam direction. The margin for respiratory-induced range uncertainties is described in Sect. 7.4.

In addition, critical normal structures (organs at risk, OARs) are also delineated on the TPS. Because OARs are likely affected by intra-/interfractional movement, patient setup error, etc., planning organ at risk volume (PRV) is delineated in addition to the ITV and PTV concepts by adding an internal margin and setup margin to OARs (Fig. 7.6). In some cases, the PTV overlaps another PTV, OAR, or PRV; however, ICRU reports 78 and 83 recommend that delineating the VOIs should not be compromised because recent TPS can optimize sufficient dose sparing of the OAR. As described here, GTV, CTV, and OAR are oncological or anatomical concepts, while ITV, PTV, and PRV are physical constructions.

7.3.2.2 Image Registration/Segmentation

The image registration/segmentation technique is mandatory in current radiotherapy procedures, particularly in treatment planning. Generally, image registration is used for contouring and 4D dose calculation. The latter is described in Sect. 7.4. Image segmentation supports the inputting of target and normal organ contours automatically (auto-contouring) without a huge burden on the oncologist. In contrast, image registration is used to transform contours between different CT data sets for the same patient and in replanning (from original CT to new CT) and 4DCT (from a reference phase to other phases). Deformable image registration (DIR) is used in place of rigid image registration to reflect realistic human geometrical changes. In treatment planning, multiple sets of image data (CT, MRI, PET, and their combinations) are generally registered. The DIR process finds a deformation vector field (DVF) between two image data sets.

DVF is obtained by applying a transforming function (generally B-spline with control points) to the reference image and calculating similarity measure between the two images. This process is repeated until the similarity measure reaches the criterion value. When the same imaging modality data set is used, image voxel values for each image data set are similar; therefore, to avoid the time-consuming in user input of further information, the intensity-based DIR method is more suitable than the landmark-based or segmentation-based methods, because it operates on image voxel values directly. Voxel similarity measure generally uses sum of squared differences and cross correlation etc.; these contours are transferred to the next image data set by applying DVF to the contours on the reference image (warping). As an example of auto-contouring in 4DCT, an oncologist manually contours one reference CT phase (generally peak exhalation), and then DIR calculates the DVF based on the 4DCT data. These are then applied to the manual contours to transform them from the reference phase to the other respiratory phases. All contours at other respiratory phases are then automatically calculated.

DIR-related auto-contouring and 4D dose calculation (described later) can have a significant impact on treatment accuracy. It is therefore important to assess registration accuracy, which is strongly dependent on patient shape. Accordingly, it is not sufficient to evaluate the registration accuracy using a phantom only.

A simple evaluation method for the registrations is visual assessment. Point landmark-based registration is performed to obtain a quantitative result, but it is substantially time-consuming and not practical in clinical settings. It is necessary to check DIR accuracy from the CT image at exhale (IM_exhale) to that at inhale (IM_inhale):

${{\mathrm{IM}}_{\mathrm{exhale}}:{\boldsymbol{x}}_{\mathrm{exhale}}\in {\Omega}_{\mathrm{exhale}},\kern0.5em \mathrm{IM}}_{\mathrm{inhale}}:{\boldsymbol{x}}_{\mathrm{inhale}}\in {\Omega}_{\mathrm{inhale}},$

(7.8)

where Ω_exhale and Ω_inhale are discrete domains of CT images at exhale and inhale and x_exhale and x_inhale are position vectors on CT images at exhale and inhale, respectively. Subtracted CT images at inhale and exhale show large differences in voxel values due to geometrical differences (Fig. 7.7a). DVF is calculated using CT images at exhale and inhale:

$\mathrm{DVF}:{\Omega}_{\mathrm{exhale}}\to {\Omega}_{\mathrm{inhale}},$

(7.9)

A warped CT image at inhale is calculated by applying DVF to the CT image at exhale. If the registration error is zero, the warped CT image and CT image at inhale are the same:

${\boldsymbol{x}}_{\mathrm{inhale}}=\mathrm{DVF}\left({x}_{\mathrm{exhale}}\right),$

(7.10)

Geometrical differences between the warped CT image and CT image at inhale are improved (Fig. 7.7b), but the registration error is not completely zero when using patient images:

${\boldsymbol{x}}_{\mathrm{inhale}}\ne \mathrm{DVF}\left({x}_{\mathrm{exhale}}\right),$

(7.11)

We then calculated another DVF (DVF’) by using the warped CT image at exhale and CT image at inhale and applied DVF’ to the warped CT image ( ${\overset{\sim }{IM}}_{exhale}$ ):

$\overset{\sim }{\mathrm{DVF}}:{\Omega}_{\mathrm{exhale}}^{\mathrm{DVF}}\to {\Omega}_{\mathrm{inhale}},$

(7.12)

${\overset{\sim }{\mathrm{IM}}}_{\mathrm{exhale}}:{\overset{\sim }{\boldsymbol{x}}}_{\mathrm{exhale}}\in {\Omega}_{\mathrm{exhale}}^{\overset{\sim }{\mathrm{DVF}}},$

(7.13)

${\overset{\sim }{\boldsymbol{x}}}_{\mathrm{exhale}}=\overset{\sim }{\mathrm{DVF}}\left[\mathrm{DVF}\left({x}_{\mathrm{exhale}}\right)\right],$

(7.14)

DIR accuracy is quantitatively visualized by the following calculation (Fig. 7.7c):

${\left\Vert \overset{\sim }{\mathrm{DVF}}\left({\overset{\sim }{\boldsymbol{x}}}_{\mathrm{exhale}}\right)-{\boldsymbol{x}}_{\mathrm{inhale}}\right\Vert}_2,$

(7.15)

where ‖∙‖ represents a norm.

Fig. 7.7

(a) Subtraction CT image at inhale from that at exhale. (b) Subtraction CT image at inhale from warped CT at inhale. (c) Magnitude of the DVF color map between CT image at inhale and warped CT image at inhale

Image registration which utilizes DIR cannot remove registration error completely, and users should therefore check the contours and modify manually if necessary. In particular, a lung DIR close to the chest wall could degrade registration accuracy, because intrafractional chest wall movement is smaller than lung motion. Biomechanical intensity-based DIR considers physical properties and in one study improved target registration error, from 1.5 ± 1.4 mm (mean ± SD) compared with conventional DIR (2.6 ± 1.4 mm) (Samavati et al. 2015). The author does not provide details of the biomechanical DIR technique here, but note that it is strongly dependent on the DIR algorithm (Brock 2010). Details about image registration can be found elsewhere (Hill et al. 2001).

7.3.3 Beam Angle Configuration

Conformal photon beam treatment planning such as IMRT generally uses more than six beam fields to reduce the doses to normal tissues, while VMAT delivers the treatment beam using a rotating gantry. The use of multiple beam fields might minimize dose errors. While a few beam fields provide good target dose conformity in particle beam therapy, dose error in respective fields should not be neglected. Given that current TPS are unable to select all beam angles automatically, treatment planners should select beam angles with consideration to the following:

1.

Avoid beam angles along the target and OAR direction to spare OARs.

This is easy to understand in the case of OARs located proximal to the target but should also be considered for OARs at the distal side. Ideally the particle beam stops at the distal edge of the target, but range uncertainty might change particle beam stopping position; an extended particle beam position might increase harmful dose to OARs located close behind the target.

2.

Opposing beam angles achieve a good biologically effective dose.

Since RBE values vary as a function of depth, opposing beam angles are not good for OAR sparing; except for tumors located around the body center, beam angles should be separated within the approximate range of 25° to 70° or something similar.

3.

Avoid inhomogeneous tissue and consider patient positional variation to minimize range uncertainty.

Small dose differences were observed between commercial TPS and Monte Carlo (MC)-derived planning, particularly for the skull and thoracic regions, which include inhomogeneous tissues (Fig. 7.8). This is because most TPSs use empirical models for dose calculation, despite the fact that the MC algorithm is much more accurate for dose calculation. Patient anatomical intra-/interfractional positional variation is a major factor in range uncertainty. An example of intrafractional beam range variation is that a single pencil beam stops at the distal edge of a tumor when passing through the heart at diastole but penetrates the tumor at systole (Fig. 7.9). Careful selection of beam angle is one solution to minimizing range uncertainties.

Fig. 7.8

Proton dose distribution calculated with a commercial TPS (XiO, Elekta Inc.) (left panel) and by Monte Carlo (MC) (right panel; Geant 4) (Adapted from Paganetti et.al. 2008)

Fig. 7.9

Carbon-ion pencil beam dose distribution at diastole and systole

4.

Consider positioning and irradiation systems restrictions.

Photon beam and proton beam treatment use rotating gantry systems to irradiate from a wide range of gantry angle. However, carbon-ion beam rotating gantry systems have not been widely adopted, although a few have been constructed in Japan and Germany. These may allow the selection of beam angles which avoid the treatment couch edge. Since most CIRT centers use a fixed beam port irradiation system, extending the range of beam angles requires the treatment couch to be rotated around the patient long axis. Planners should leave this part in the tip of the corner.

7.3.4 Irradiation Method

This section provides a brief technical overview of the two most common irradiation techniques used in CIRT, passive scattering, and pencil beam scanning (PBS).

The passive scattering irradiation technique has been long and widely used in charged particle beam therapy, including proton and carbon-ion beams. A pristine beam with a narrow beam width in both lateral and depth directions is extracted from the accelerator. To cover the whole target volume, the pristine beam should be spread out in both directions. First, a wobbler magnet and scattering system are used to laterally and uniformly spread the pristine beam (Fig. 7.10a). Second, a ridge filter modulates the beam energy to obtain a uniform biological dose distribution along depth direction SOBP. Third, a patient collimator (PTC) and/or multi-leaf collimator (MLC) are used to adjust the beam to the target volume laterally. Finally, a compensator bolus adjusts the beam stopping position at the distal edge of the target. This method provides good dose conformity for the distal region of the target, but cannot avoid an unnecessarily high dose around the proximal side of the target.

Fig. 7.10

Schematic drawing of (a) passive scattering, (b) layer-stacking, and (c) scanning irradiation techniques. Dotted curved lines show the iso-energy layers

The layer-stacking irradiation technique was developed in 1983 with the aim of maximizing dose conformation and minimizing the dose to normal tissue around the proximal side of the target with scattering beams, similar to that with PBS irradiation. It is now in clinical use at a few carbon-ion beam treatment centers (Kanai et al. 1983; Kanematsu et al. 2002). Uniform dose within the target is achieved by combining a number of small SOBPs along a depth direction. These small SOBP positions are shifted by changing range shifters (Fig. 7.10b). Beam field size is defined to fit the respective iso-energy layer regions by changing the MLC opening width.

With regard to PBS, this method was first proposed in the 1980s at NIRS, and carbon-ion PBS (C-PBS) was first implemented clinically at the Gesellschaft für Schwerionenforschung (GSI) in Darmstadt, Germany (Kanai et al. 1980; Haberer et al. 1993). Worldwide, a few treatment centers were using C-PBS as of 2015. The pencil beam is scanned in all three dimensions over the spot positions of the target to achieve a uniform dose within the target (Fig. 7.10c). Since PBS has a flexible dose distribution, OAR sparing is better than with passive scattering irradiation, and an inhomogeneous dose distribution (e.g., IMPT, additional doses to hypoxic regions) can be achieved. MLC, PTC, and a compensator bolus are not required, eliminating the treatment workflow time normally required to change these accessories and minimizing therapist entry into the treatment room. The beam energy is changed with a range shifter and/or accelerator change. A major problem with the use of a thicker range shifter is that it causes a broadening of the beam spot size with increasing depth through range shifters. By contrast, active change using an accelerator takes energy change time and requires a massively extended commissioning time for each beam energy (over a few hundred beam energies). Hybrid depth scanning with a synchrotron was developed to overcome these problems. Hybrid depth scanning provides a smaller lateral dose fall off and RBE than range shifter scanning (Inaniwa et al. 2012) and uses the range shifter to shift the small SOBPs at a step size of 3 mm in combination with 11 distinct synchrotron energies (Fig. 7.11).

Fig. 7.11

C-PBS dose distributions in the depth direction (D_p), lateral direction (σ), and normalized fluence for RS, ES, and HS, respectively (With permission from Inaniwa et al. 2012)

7.3.5 Dose Calculations

7.3.5.1 Beam Range Calculation

Beam spot positions are set on steps of a few millimeters (generally 2–3 mm, depending on C-PBS beam size) on CT images. Water equivalent path length (WEPL) from the irradiation system (scanning magnet) to respective spots is calculated by integrating the stopping effective density along each ray line:

$\mathrm{WEPL}(z)={\int}_0^z{\rho}_s\left({z}^{\prime}\right)\mathrm{d} z^{\prime },$

(7.16)

where z is the total penetration depth, z’ is the penetration depth, and ρ _sis the stopping power.

For the square-shaped case in Fig. 7.12, the same WEPL position (iso-energy layer) (shown as dotted lines) is oriented in a horizontal line (Fig. 7.12a). Most distal spot positions (red circles in Fig. 7.12a) are irradiated by the same energy beam. For the spherically shaped case, in contrast, the iso-energy layer position is curved and not the same as the target shape (Fig. 7.12b). Most distal spot positions (red circles in Fig. 7.12b) are irradiated by different beam energies. In a more realistic case (lung case), the tissue density for lung may be decreased from approximately 1.0 g/cm³ to 0.3 g/cm³, potentially exerting a strong impact on the iso-energy layer position by making it more complex. To understand this more clearly, the lung CT image is transformed in the same WEPL value positions in Fig. 7.12d; compared to the original lung CT (Fig. 7.12c), the geometrical shape is substantially deformed, and the lung thickness is substantially shortened in the WEPL coordinate. C-PBS doses are calculated in respective beam spots.

Fig. 7.12

Schematic diagram of the beam spot position in several iso-energy layers for (a) rectangular shape and (b) spherical shape. Iso-energy layer number was assigned from the distal side (With permission from ICRU-72 2007). Lung CT images in coronal section in (c) CT and (d) WEPL coordinates

7.3.5.2 Beam Modeling

For the C-PBS beam model, lateral dose distribution can be approximated by the Gaussian function as a function of penetration depth. Accumulated dose distribution in the PBS irradiation is superimposed on the respective pencil beam dose distributions, meaning that beam field size would be varied at the respective iso-energy layers. The dependence of photon and particle beam doses on beam field size is well known and is likely emphasized in PBS irradiation. However, a single Gaussian model does not completely compensate for the field size effect. Proton beam lateral distribution can be expressed by the sum of two Gaussians: the first and second components are the primary proton and nuclear beam halo, respectively (Pedroni et al. 2005). For carbon-ion beams, three Gaussians are used to accurately model the lateral distributions on account of nuclear fragments; the first component is primary carbon ion, the second is heavy fragments, and the third is light fragments (Inaniwa et al. 2009; Kusano et al. 2007) (Fig. 7.13), and the ith PBS dose distribution (d _i(x,y,z)) is expressed by the following:

$\begin{array}{ll}{d}_i\left(x,y,z\right)=& {d}_{z,i}(z)\hfill \\ {}& \times \left\{\left(1-\sum_{j=2}^3{f}_{j,i}(z)\right){D}_{1,i}\left(x,y,{\sigma}_{1,i}(z)\right)+\sum_{j=2}^3{f}_{j,i}(z){D}_{j,i}\left(x,y,{\sigma}_{j,i}(z)\right)\right\}\kern0.5em ,\hfill \end{array}$

(7.17)

where d _z.,i(z) and σ _j,i(z) are the integral dose and standard deviation at a penetration depth z, respectively; D _j,i(x,y, σ _j,i(z)) is a two-dimensional Gaussian function for the lateral distribution of the jth component; and f _j,i(z) is the fraction of integrated dose of the jth Gaussian component. Physical dose distribution for PBS (D _phys) is composed by summing the respective pencil beam doses:

${D}_{\mathrm{phys}}\left( x, y, z\right)=\sum_{i=1}^N{d}_i\left( x, y, z\right)\bullet {w}_i,$

(7.18)

where N is the total number of spots and w _iis the ith beam spot weight.

Fig. 7.13

(a) Lateral beam spreads of the first, second, and third components for the range shifter thicknesses of 0, 50, and 100 mm WEL. (b) Fraction factors of the second and third components for the range shifter thicknesses of 0, 50, and 100 mm WEL (Reproduced from Inaniwa et al. 2009)

7.3.5.3 Biological and Clinical Doses

Since biological effect in heavy charged particle therapy is strongly dependent on particle type, the primary particle and all fragment particles produced during the stopping process should be considered (Schardt et al. 2010). To discriminate the physical dose (Gy), ICRU recommends use of the term “RBE-weighted” dose (Gy (RBE)) for biological dose (ICRU-72 2007). Biological dose distribution is expressed as a typical tumor cell response, as defined by the in vitro response of human salivary gland (HSG) tumor cells. A German group adapted the local effect model (LEM) to CIRT (Elsasser et al. 2008). Another model was introduced as the microdosimetric kinetic model (MKM), which predicts the survival fraction of cells from the specific energy absorbed by a microscopic subcellular structure (Hawkins 1996; Hawkins 2003). However, MKM does not perfectly predict RBE due to insufficient overkill correction in high-energy regions (LET >100 keV/μm). To solve this problem, Kase et al. adapted saturation correction to express the decrease in RBE due to the overkill effect in a mixed radiation field (modified MKM) (Kase et al. 2006b). The modified MKM provides RBE values from proton to silicon using a linear quadratic (LQ) function, which simplifies the calculation of RBE under the mixed radiation field (Kase et al. 2006a) (Fig. 7.14).

Fig. 7.14

Relationship between experimental α value and the saturation-corrected dose-mean lineal energy (With permission from Kase et al. 2006a)

Biological dose in the mixed radiation field is expressed as follows:

${D}_{\mathrm{biol}}\left( x, y, z\right)={D}_{\mathrm{phys}}\left( x, y, z\right)\bullet {RBE}_{\mathrm{biol}}\left( x, y, z\right)=-\frac{\alpha}{2\beta}+\sqrt{{\left(\frac{\alpha}{2\beta}\right)}^2-\frac{ \ln S\left({D}_{\mathrm{phys}}\left( x, y, z\right)\right)}{\beta}},$

(7.19)

$\ln \left( S\left({D}_{\mathrm{phys}}\left( x, y, z\right)\right)\right)=-\left({\alpha}_0+\beta {z}_{1 D\ \mathrm{mix}}^{*}\left( x, y, z\right)\right){D}_{\mathrm{phys}}\left( x, y, z\right)-\beta {D_{\mathrm{phys}}\left( x, y, z\right)}^2,$

(7.20)

where α and β are the coefficients of the LQ model for the reference radiation and α ₀is the initial slope of the surviving fraction curve in the limit of LET = 0. β value is independent of radiation type and is selected as 0.0615Gy^-2 based on the β value of HSG cells irradiated by X-ray (Furusawa et al. 2000). To predict RBE in the mixed radiation field, the saturation-corrected dose means that a single energy extended to the saturation-corrected dose-mean specific energy ( ${z}_{1 D\ mix}^{*}$ ), which can be derived by MC and the Kiefer-Chatterjee model (Kiefer and Straaten 1986), must be calculated (Fig. 7.15). Details for calculating the saturation-corrected dose-mean specific energy are described in Inaniwa et al. (2010):

${z}_{1 D\ \mathrm{mix}}^{*}\left( x, y, z\right)=\frac{\sum_{i=1}^N{w}_i\bullet {d}_i\left( x, y, z\right)\bullet {\overset{-}{z}}_{1 D: i}^{*}(z)}{\sum_{i=1}^N{w}_i\bullet {d}_i\left( x, y, z\right)},$

(7.21)

where ${\overset{-}{z}}_{1 D: i}^{*}(z)$ is the saturation-corrected dose-mean specific energy delivered by the jth beam. To adapt biological response in vitro to patient treatment (in vivo), the biological dose should be rescaled by multiplying by a clinical factor (F _clin). Clinical dose can be calculated by the following:

${D}_{\mathrm{clin}}\left( x, y, z\right)={D}_{\mathrm{bio}}\left( x, y, z\right)\bullet {F}_{\mathrm{clin}},$

(7.22)

The clinical factor of 2.41 is used in our facility. Due to word count limitations, details and historical background are provided elsewhere (Kanematsu et al. 2002; Kanai et al. 1999; Inaniwa et al. 2015).

Fig. 7.15

(a) C-PBS depth dose distributions and (b) the saturation-corrected dose-mean specific energy of the domain of a 290 MeV/u for range shifter thicknesses of 0, 30, 60, and 90 mm (With permission from Inaniwa et al. 2010)

7.3.5.4 Dose Optimization

To achieve the desired target conformation and OAR sparing doses, respective beam spot weights are optimized by an iterative process (inverse planning). Generally, the objective function ( f(w)) is defined as the errors between the current target dose and the maximum/minimum target doses (Bortfeld et al. 1990) as follows:

$$$ f(w)=\sum_{i\in \mathrm{target}}\begin{array}{c}\left({\alpha}_{\mathrm{under}}^{\mathrm{target}}{\left[{D}_{\min}^{\mathrm{target}}-{D}_i(w)\right]}^2+{\alpha}_{\mathrm{over}}^{\mathrm{target}}{\left[{D}_i(w)-{D}_{\max}^{\mathrm{target}}\right]}^2\right)\kern0.75em \\ {}\underset{w>0}{\mathrm{minimum}}\ f(w)\kern0.5em \end{array}, $$ ” src=”https://radiologykey.com/wp-content/uploads/2017/07/A340376_1_En_7_Chapter_Equ23.gif”></DIV></DIV><br /> <DIV class=EquationNumber>(7.23)</DIV></DIV>where the operator [ ] is the Heaviside step function. <SPAN class=EmphasisTypeItalic>w</SPAN> is the vector notation of the beam weights for all pencil beams; <SPAN class=EmphasisTypeItalic>D</SPAN> <SUB><SPAN class=EmphasisTypeItalic>i</SPAN> </SUB>(<SPAN class=EmphasisTypeItalic>w</SPAN>) is the dose at the <SPAN class=EmphasisTypeItalic>i</SPAN>th spot position; <SPAN id=IEq4 class=InlineEquation><IMG alt=$ and ${D}_{\min}^{\mathrm{target}}$ are user-defined maximum and minimum doses in the target, respectively; and ${\alpha}_{\mathrm{under}}^{\mathrm{target}}$ and ${\alpha}_{over}^{target}$ are the penalties for target underdosage and overdosage, respectively.

If dose constraint to the target and OAR is considered (maximum dose constraint, minimum dose constraint, dose volume constraint, etc.), these constraint mathematical expressions should be added to the objective functions. To find the optimum solutions, several types of optimization strategy have been introduced.

1.

Gradient descent

The gradient descent method calculates the direction (d) with a large magnitude of the negative gradient at the current value (series of point, p) (kth iteration). A learning rate (τ) adjusts the step size to search for the next value: