64 Diffusion Tensor Imaging
Diffusion-weighted imaging (DWI) is a critical tool for the MR assessment of ischemic changes of the brain and in the differential diagnosis of cystic brain lesions. Diffusion tensor imaging (DTI), which provides additional information beyond that available from conventional DWI, is a promising new noninvasive method for studying whitematter structure of the human brain in vivo. The basis of the signal measured in a diffusion-weighted MRI experiment is the Brownian motion of water protons. Brownian movement is the random movement of particles based on their thermal energy. This movement is also referred to as diffusion; hence the technique is named diffusion-weighted imaging.
In a static, homogeneous magnetic field, all protons precess with the same frequency. If a gradient (a temporary magnetic field) is turned on, this homogeneity can be disturbed in a known fashion and the signal from the object in the scanner decreases. This first step of diffusion preparation is called dephasing. If this gradient is followed by a gradient with opposite direction, the signal can be restored, the so-called rephasing. If protons move between dephasing and rephasing, the restoration of the signal is incomplete. The more movement, the more signal loss. In this fashion, MRI can be sensitized to diffusion. The strength of diffusion weighting is dependent upon the gradient strength, duration of and time between the dephasing and rephasing gradients, and is summarized in the so-called b-value. The higher the b-value, the stronger is the diffusion weighting. Typical b-values for DTI of the brain vary between 600 and 1000 sec/mm2, with clinical DWI performed usually with a b-value of 1000.
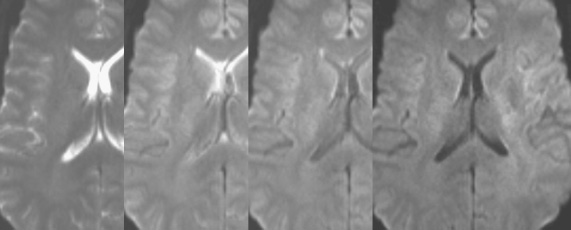
As can be seen in Fig. 64.1 (b values of 0, 300, 600, and 900 are illustrated in a normal volunteer), the stronger the diffusion weighting, the greater the signal loss in areas with strong free motion (e.g., the ventricle). The apparent diffusion coefficient (ADC) is calculated by measuring the signal loss when comparing the non-diffusion-weighted image with the weighted image. To calculate a direction invariant ADC, the diffusion weighting is performed in three main axes. Thus, to obtain an ADC map, a minimum of four data sets (one nonweighted and three weighted) are required.