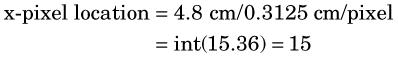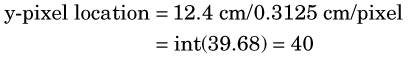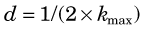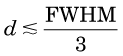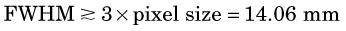1 Basic Characteristics and Terminology

For many years, nuclear medicine images were produced directly on film, by exposing the film to a light source that produced flashes of light when radiations were detected by the imaging instrument. As with ordinary photographs, the image was recorded with a virtually continuous range of brightness levels and x-y locations on the film. Such images sometimes are referred to as analog images. Very little could be done in the way of “image processing” after the image was recorded.

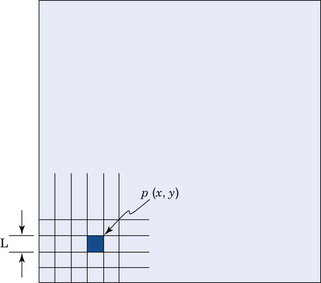
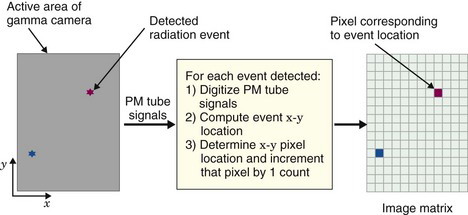
Virtually all modern nuclear medicine images are recorded as digital images. This is required for computerized image processing. A digital image is one in which events are localized (or “binned”) within a grid comprising a finite number of discrete (usually square) picture elements, or pixels (Fig. 20-1). Each pixel has a digital (nonfractional) location or address, for example, “x = 5, y = 6.” For a gamma camera image, the area of the detector is divided into the desired number of pixels (Fig. 20-2). For example, a camera with a field-of-view of 40 cm × 40 cm might be divided into a 128 × 128 grid of pixels, with each pixel therefore measuring 0.3125 mm × 0.3125 mm. Each pixel corresponds to a range of possible physical locations within the image. If an event were determined to have interacted at a location x = 4.8 cm, y = 12.4 cm, the appropriate pixel location for this event would be

FIGURE 20-1 A digital image consists of a grid or matrix of pixels, each of size L × L units. Each pixel has an x-y address location, with pixel value, p(x,y), corresponding to the number of counts or other quantity associated with that pixel.

FIGURE 20-2 Subdivision of the gamma camera detector area for generating a digital image. The photomultiplier tube signals are analyzed using analog-to-digital converters to assign the digital matrix location for each detected event.

where int(x) denotes the nearest integer of x, and the pixels are labeled from 0-127 with the coordinate system defined as shown in Figure 20-2.

A similar format is used for digital multislice tomographic images, except that the discrete elements of the image would correspond to discrete 3-D volumes of tissue within a cross-sectional image. The volume is given by the product of the x- and y-pixel dimensions multiplied by the slice thickness. Thus they are more appropriately called volume elements, or voxels. However, when discussing an individual tomographic slice, the term pixel still is commonly used. In tomographic images, the “intensity” of each voxel may or may not have a discrete integer value. For example, voxel values for a reconstructed image will generally have noninteger values corresponding to the calculated concentration of radionuclide within the voxel.

Depending on the mode of acquisition (discussed in Section A.4), either the x-y address of the pixel in which each event occurs, or the pixel value, p(x, y), is stored in computer memory. For 3-D imaging modes, such as 3-D SPECT or PET, individual events are localized within a 3-D matrix of voxels, and the reconstructed value in a voxel is denoted as v(x, y, z). Depending on how data are acquired and processed by the imaging system, the pixel or voxel value may correspond to the number of counts, counts per unit time, the reconstructed pixel or voxel value, or absolute radionuclide concentrations (kBq/cc or µCi/cc).

Although most interactions between the user and a computer system involve conventional decimal numbers, the internal operations of the computer usually are performed using binary numbers. Binary number representation uses powers of 2, whereas the commonly used decimal number system uses powers of 10. For example, in decimal representation, the number 13 means [(1 × 10¹) + (3 × 10⁰)]. In the binary number system, the same number is represented as 1101, meaning [(1 × 2³) + (1 × 2²) + (0 × 2¹) + (1 × 2⁰)], or (8 + 4 + 0 + 1) = 13. Each digit in the binary number representation is called a bit (an abbreviation for “binary digit”). In general, an n-bit binary number can represent decimal numbers with values between zero and (2ⁿ − 1).

Binary numbers are employed in computer systems because they can be represented conveniently by electronic components that can exist only in an “on” or “off” state. Thus an n-bit binary number can be represented by the “on” or “off” state of a sequence of n such components. To communicate sensibly with the outside world, the binary numbers used within the computer must be converted into decimal integers or into decimal numbers and fractions. The latter are called floating point numbers. The methods by which binary numbers are converted to decimal format are beyond the scope of this presentation and can be found in more advanced texts on computer systems.

Digital images are characterized by matrix size and pixel depth. Matrix size refers to the number of discrete picture elements in the matrix. This in turn affects the degree of spatial detail that can be presented, with larger matrices generally providing more detail. Matrix sizes used for nuclear medicine images typically range from (64 × 64) to (512 × 512) pixels. Matrix size virtually always involves a power of 2 (2⁶ and 2⁹ in the previous examples) because of the underlying binary number system used in the computer.

Pixel depth refers to the maximum number of events that can be recorded per pixel. Most systems have pixel depths ranging from 8 bits (2⁸ = 256; counts range from 0 to 255) to 16 bits (2¹⁶ = 65,536; counts range from 0 to 65,535). Note again that these values are related to the underlying binary number system used in the computer. When the number of events recorded in a pixel exceeds the allowed pixel depth, the count for that pixel is reset to 0 and starts over, which can lead to erroneous results and image artifacts.

Pixel depth also affects the number of gray shades (or color levels) that can be represented within the displayed image. In most computer systems in use in nuclear medicine, 8 bits equals a byte of memory and 16 bits equals a word of memory. The pixel depth, therefore, frequently is described as “byte” mode or “word” mode.*

2 Spatial Resolution and Matrix Size

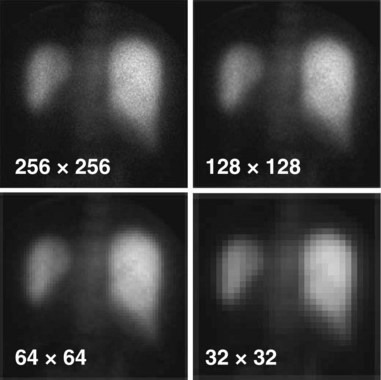
The spatial resolution of a digital image is governed by two factors: (1) the resolution of the imaging device itself (such as detector or collimator resolution) and (2) the size of the pixels used to represent the digitized image. For a fixed field-of-view, the larger the number of pixels, that is, the larger the matrix size, the smaller the pixel size (Fig. 20-3). Clearly, a smaller pixel size can display more image detail, but beyond a certain point there is no further improvement because of resolution limitations of the imaging device itself. A question of practical importance is, At what point does this occur? That is, how many pixels are needed to ensure that significant detail is not lost in the digitization process?

FIGURE 20-3 Digital images of the liver and spleen (posterior view) displayed with different matrix sizes. The larger the matrix size, the smaller the pixels and the more detail that is visible in the image.

(Original image courtesy GE Medical Systems, Milwaukee, WI.)

The situation is entirely analogous to that presented in Chapter 16 for sampling requirements in reconstruction tomography. In particular, Equation 16-13 applies—that is, the linear sampling distance, d, or pixel size, must be smaller than or equal to the inverse of twice the maximum spatial frequency, k_max, that is present in the image:

(20-1)

This requirement derives directly from the sampling theorem discussed in Appendix F, Section C.

Once this sampling requirement is met, increasing the matrix size does not improve spatial resolution, although it may produce a cosmetically more appealing image with less evident grid structure. If the sampling requirements are not met (too coarse a grid), spatial resolution is lost. The maximum spatial frequency that is present in an image depends primarily on the spatial resolution of the imaging device. If the resolution of the device is specified in terms of the full width at half maximum (FWHM) of its line-spread function (Chapter 15, Section B.2), then the sampling distance (pixel size) should not exceed about one third of this value to avoid significant loss of spatial resolution, that is,

(20-2)

This applies for noise-free image data. With added noise it may be preferable to relax the sampling requirement somewhat (i.e., use larger pixels) to diminish the visibility of noise in the final digitized image.

Example 20-1

What is the approximate spatial resolution that can be supported for a 30-cm diameter field-of-view using a 64 × 64 matrix? A 128 × 128 matrix? Assume that the original data are noise free.

Answer

64 × 64 matrix

A 64 × 64 image matrix results in a pixel size of 300 mm/64 = 4.69 mm. From Equation 20-2, this would be suitable for image resolution given by

128 × 128 matrix

The values calculated in Example 20-1 represent the approximate levels of imaging system resolution that could be supported without loss of imaging resolution for the specified image and matrix sizes. The practical effects of undersampling depend as well on the information contained in the image and whether it has a significant amount of actual spatial frequency content near the resolution limit of the imaging device. Practical experimentation sometimes is required to determine this for a particular type of imaging procedure.

3 Image Display

Digital images in nuclear medicine are displayed on cathode ray tubes (CRTs) or flat-panel displays such as liquid crystal displays (LCDs). In addition to their use at the site of the imaging device, displays are an essential component of picture archival communications systems (PACS) networks, for remote viewing of images (see Section C). The spatial resolution of the display device should exceed that of the underlying images so as not to sacrifice image detail. In general, the display devices used in nuclear medicine computer systems and in radiology-based PACS networks comfortably exceed this requirement. Typical high-resolution CRTs have 1000 or more lines and a typical LCD might have 1536 × 2048 elements.

Individual pixels in a digital image are displayed with different brightness levels, depending on the pixel value (number of counts or reconstructed activity in the pixel) or voxel value. On grayscale displays, the human eye is capable of distinguishing approximately 40 brightness levels when they are presented in isolation and an even larger number when they are presented in a sequence of steps separated by sharp borders. Image displays are characterized by the potential number of brightness levels that they can display. For example, an 8-bit grayscale display can potentially display 2⁸ = 256 different brightness levels. Such a range is more than adequate in comparison with the capabilities of human vision. In practice, the effective brightness scale often is considerably less than the physical limits of the display device because of image noise. For example, if an image has a root mean square noise level of 1%, then there are not more than 100 significant brightness levels in the image, regardless of the capabilities of the display device.

Digital images also can be displayed in color by assigning color hues to represent different pixel values. The human eye can distinguish millions of different colors, and color displays are capable of producing a broader dynamic range (i.e., number of distinguishably different levels) than can be achieved in black-and-white displays. For example, a true-color

Related posts:

The Gamma Camera: Basic Principles Modes of Radioactive Decay Counting Systems Single Photon Emission Computed Tomography Decay of Radioactivity Positron Emission Tomography

Stay updated, free articles. Join our Telegram channel

Join