Author (year)
N
Total dose (Gy)
Daily dose (Gy)
Reference point
Local control
Median follow-up
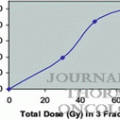
Arimoto et al. (1998) [3]
24
60
7.5
Isocenter
92 % (not described)
24 months
Uematsu et al. (2001) [4]
50
50–60
10
80 % Margin
94 % (follow-up period)
36 months
Wulf et al. (2004) [5]
20
45–56.2
15–15.4
80 % Margin
95 % (1 year)
10 months
Nagata et al. (2005) [6]
45
48
12
Isocenter
97 % (follow-up period)
30 months
Xia et al. (2006) [7]
43
70(50)
7(5)
Isocenter
95 % (3 years)
27 months
Baumann et al. (2009) [8]
57
45
15
67 % Margin
92 % (3 years)
35 months
Timmerman et al. (2010) [9]
55
54
18
80 % Margin
98 % (3 years)
34 months
Nagata et al. (2010) [10]
64
48
12
Isocenter
69 % (6 years)
45 months
Examples of organ dose constraints used in major trials in Japan, North America, RTOG (Radiation Therapy Oncology Group) trial, and the international STARS (Study of Anastrozole and Radiotherapy Sequencing) trial are presented in Table 8.2 [11–13]. Note that these dose constraints will likely change as clinical experience with SBRT increases. Moreover, the toxicity depends on the total dose and fraction size of the SBRT treatment. By modulating these parameters, the rates of adverse effects can be lowered and greater flexibility can be achieved in regions amenable to SBRT.
Table 8.2
Dose constraints used in Japan, major North American, and international trials
Organ at risk | JCOG 0403 (4 fractions) | RTOG 0618 (3 fractions) | International STARS trial (4 fractions) |
|---|---|---|---|
Lung | 40 Gy ≤ 100 cc | V20 ≤ 10 % | V20 ≤ 20 % |
Mean dose ≤18 Gy | V10 ≤ 30 % | ||
V20 ≤ 20 % | V5 ≤ 50 % | ||
V15 ≤ 25 % | |||
Spinal cord | ≤25 Gy | ≤18 Gy | 20 Gy ≤ 1 cc |
15 Gy ≤ 10 cc | |||
Esophagus | 40 Gy ≤ 1 cc | ≤27 Gy | 40 Gy ≤ 1 cc |
35 Gy ≤ 10 cc | 35 Gy ≤ 10 cc | ||
Trachea | 40 Gy ≤ 10 cc | ≤30 Gy | 35 Gy ≤ 1 cc |
30 Gy ≤ 10 cc | |||
Bronchi | 40 Gy ≤ 10 cc | ≤30 Gy | 40 Gy ≤ 1 cc |
35 Gy ≤ 10 cc | |||
Skin | ≤40 Gy | ≤24 Gy | 40 Gy ≤ 1 cc |
35 Gy ≤ 10 cc |
Since SBRT was included in the Japanese national health insurance system in 2004, the number of institutions performing SBRT increased rapidly. The clinical trials for SBRT have been performed for the safety radiation treatment in Japan. According to the Japan Clinical Oncology Group (JCOG) 0403 protocol, the dose prescription is defined as the point dose at the isocenter of the planning target volume (PTV) with inhomogeneity correction, such as the pencil beam convolution with Batho power law or the Clarkson with effective path length correction. Unfortunately, this prescription is not accurate for dose calculations in lung cancer [14]. In the isocenter prescription, a total dose of 48 Gy at the isocenter is delivered with a daily dose of 12 Gy in four fractions within a 2-week period. The PTV prescription was adopted in the JCOG 0702 phase I trial instead of the isocenter prescription, which was adopted in the previous JCOG 0403 phase II trial. In the JCOG 0702 protocol, a inhomogeneity correction algorithm, which is equivalent to superposition algorithms, is required for dose calculation. Additionally, in the prescription method, the International Commission on Radiation Units and Measurements (ICRU) recommended methods of dose prescription have been changed from prescription at the isocenter point of the treatment plan to prescription at the periphery of the PTV [15]. Therefore, the dose prescription protocol of SBRT should be prepared by sufficiently considering the irradiation technology, IGRT, and dose calculation algorithm for each facility.
8.3 Dose Calculation
The American Association of Physicists in Medicine (AAPM) Task Group #65 (TG-65) recommended that computed dose distributions should be accurate to 1 % or 2 % [16]. Dose calculation algorithms for radiation therapy have improved to achieve this accuracy level. In SBRT, the presence of heterogeneous tissue (e.g., lung tissue surrounding thoracic tumors) and the use of a smaller field size confound radiation dose computation. Moreover, small-field conditions often occur as a result of transient electronic disequilibrium. In low-density tissues such as the lungs, the re-buildup effect produces underdosage near the tumor interface due to the increasing electron range with increasing energy. The effects of transient electronic disequilibrium and increased electron range in low-density tissues will reduce the central-axis dose beyond an air cavity and potentially result in an underdosage of the tumor [17].
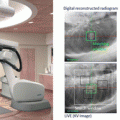
The development of model-based convolution methods has significantly improved the accuracy of dose calculations for such heterogeneous tissues when compared to correction-based methods [18, 19]. Model-based convolution method use physical principles, which describe the actual physical transport in the tissue, to calculate the dose (Fig. 8.1). Monte Carlo-based methods and the grid-based Boltzmann equation solver (GBBS) method provide more accurate dose distributions. In this section, we describe the most widely used algorithms for radiation treatment planning such as the convolution method, convolution/superposition method, Monte Carlo method, and GBBS method.
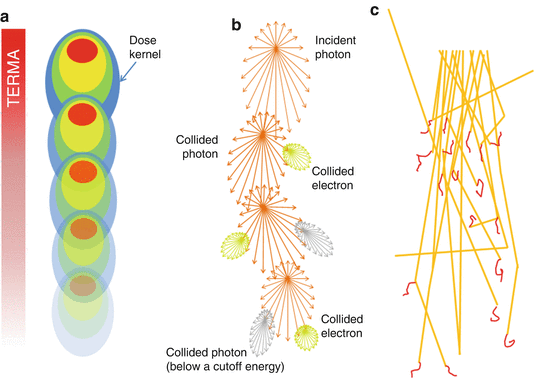

Fig. 8.1
Dose calculation algorithm comparison (a) Convolution/superposition method (b) GBBS method (c) Monte Carlo method
8.3.1 Convolution Method
The convolution method was proposed by Mackie et al. [20] in 1985. In essence, the energy fluence distribution is convolved with the scatter-spread kernel to obtain the dose. One of the commonly used convolution method in commercial treatment planning systems (TPSs) is pencil beam convolution (PBC) [18]. In the convolution method, the absolute dose at point 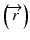 is given by:
is given by:
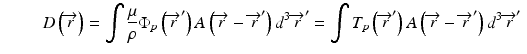
where μ/ρ is the mass attenuation coefficient, 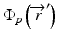 is the primary photon fluence,
is the primary photon fluence, 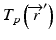 is the primary energy fluence, known as Terma, and
is the primary energy fluence, known as Terma, and 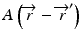 is the pencil beam kernel. The pencil beam kernels represent the absorbed dose distribution in water for a very small beam obtained by the deconvolution of basic measurement data or by Monte Carlo method calculations. Although the PBC methods are generally fast, the accuracy is compromised in the presence of heterogeneous tissue.
is the pencil beam kernel. The pencil beam kernels represent the absorbed dose distribution in water for a very small beam obtained by the deconvolution of basic measurement data or by Monte Carlo method calculations. Although the PBC methods are generally fast, the accuracy is compromised in the presence of heterogeneous tissue.
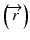 is given by:
is given by: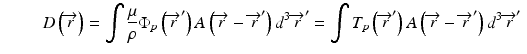
(8.1)
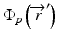 is the primary photon fluence,
is the primary photon fluence, 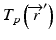 is the primary energy fluence, known as Terma, and
is the primary energy fluence, known as Terma, and 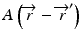 is the pencil beam kernel. The pencil beam kernels represent the absorbed dose distribution in water for a very small beam obtained by the deconvolution of basic measurement data or by Monte Carlo method calculations. Although the PBC methods are generally fast, the accuracy is compromised in the presence of heterogeneous tissue.
is the pencil beam kernel. The pencil beam kernels represent the absorbed dose distribution in water for a very small beam obtained by the deconvolution of basic measurement data or by Monte Carlo method calculations. Although the PBC methods are generally fast, the accuracy is compromised in the presence of heterogeneous tissue.8.3.2 Convolution/Superposition Method
When the convolution method is modified to incorporate the density-base scaling of both the primary fluence and electron scatter in heterogeneous tissue, it is called the convolution/superposition method [21]. The absolute dose at point 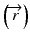 is given by:
is given by:
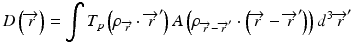
where 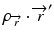 is the radiologic path length from the source to primary photon interaction site, and
is the radiologic path length from the source to primary photon interaction site, and 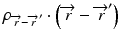 is the radiologic path length from the primary photon interaction site to the dose deposition site. In general, the effective density calculated along the scattered ray path is used to change secondary particle contributions or to assign the appropriate value in the scatter kernel using density scaling [16]. Both the convolution/superposition and Clarkson/pencil beam algorithms are well matched at the PTV center embedded in the tissue; however, significant differences exist in the target periphery [22]. Consequently, the analytical anisotropic algorithm (AAA) implemented in the Eclipse Varian Medical Systems TPS is a convolution/superposition method [18, 23, 24]. AAA should provide a better modeling of the dose deposition in the lung and at the interfaces of lung-tumor or lung-tissue [24].
is the radiologic path length from the primary photon interaction site to the dose deposition site. In general, the effective density calculated along the scattered ray path is used to change secondary particle contributions or to assign the appropriate value in the scatter kernel using density scaling [16]. Both the convolution/superposition and Clarkson/pencil beam algorithms are well matched at the PTV center embedded in the tissue; however, significant differences exist in the target periphery [22]. Consequently, the analytical anisotropic algorithm (AAA) implemented in the Eclipse Varian Medical Systems TPS is a convolution/superposition method [18, 23, 24]. AAA should provide a better modeling of the dose deposition in the lung and at the interfaces of lung-tumor or lung-tissue [24].
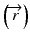 is given by:
is given by: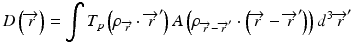
(8.2)
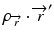 is the radiologic path length from the source to primary photon interaction site, and
is the radiologic path length from the source to primary photon interaction site, and 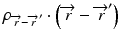 is the radiologic path length from the primary photon interaction site to the dose deposition site. In general, the effective density calculated along the scattered ray path is used to change secondary particle contributions or to assign the appropriate value in the scatter kernel using density scaling [16]. Both the convolution/superposition and Clarkson/pencil beam algorithms are well matched at the PTV center embedded in the tissue; however, significant differences exist in the target periphery [22]. Consequently, the analytical anisotropic algorithm (AAA) implemented in the Eclipse Varian Medical Systems TPS is a convolution/superposition method [18, 23, 24]. AAA should provide a better modeling of the dose deposition in the lung and at the interfaces of lung-tumor or lung-tissue [24].
is the radiologic path length from the primary photon interaction site to the dose deposition site. In general, the effective density calculated along the scattered ray path is used to change secondary particle contributions or to assign the appropriate value in the scatter kernel using density scaling [16]. Both the convolution/superposition and Clarkson/pencil beam algorithms are well matched at the PTV center embedded in the tissue; however, significant differences exist in the target periphery [22]. Consequently, the analytical anisotropic algorithm (AAA) implemented in the Eclipse Varian Medical Systems TPS is a convolution/superposition method [18, 23, 24]. AAA should provide a better modeling of the dose deposition in the lung and at the interfaces of lung-tumor or lung-tissue [24].Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree