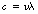Chapter 17 Electromagnetic radiation
Chapter contents
17.1 Aim
This chapter discusses the properties of electromagnetic radiations. The wave–particle duality of such radiations will be further discussed. Having identified the contents of the electromagnetic spectrum, we will finally consider some parts of this spectrum in more detail as these are of particular relevance to radiography.
17.2 Introduction
As can be seen from Figure 17.3 (p. 114), the electromagnetic spectrum encompasses a wide range of radiation types and we are only sensitive to a small section of these radiations. We can see the world around us because the retinas of our eyes are sensitive to a section of the electromagnetic spectrum which we know as light. Similarly, we can feel heat from the sun because our skin responds to the infrared part of the electromagnetic spectrum. We can also accidentally walk through a beam of X-rays or handle an isotope which is producing gamma radiation because none of our sense organs are able to detect them. It is important to remember, when we consider radiation protection, that although our sense organs are not able to detect the presence of ionizing radiations (X or gamma), they may still be damaged by them.
17.3 Properties of electromagnetic radiations
All electromagnetic radiations exhibit a set of general properties which are listed below:
• The waves are composed of transverse vibrations of electric and magnetic fields. (Transverse vibrations are ones which are oscillating at right angles to the direction of travel.)
• The vibrations have a wide range of wavelengths and frequencies.
• All electromagnetic radiations travel through a vacuum with the same velocity: 3×108 m.s−1.
• All electromagnetic radiations travel in straight lines.
• The radiations are unaffected by electric or magnetic fields.
• The radiations may be polarized so that they vibrate in one plane only.
• The radiations are able to produce constructive or destructive interference.
• All the radiations obey the duality principle (see Sect. 16.6) and so can either be considered as waves or as quanta with energy and momentum.
From the above list it is obvious that all electromagnetic radiations have a lot in common, so how can they be used for such widely differing purposes? The answer to this lies in the differences which they exhibit in their interactions with matter. These are outlined in Table 17.1.
Table 17.1 Interactions of different electromagnetic radiations with matter
| INTERACTION | NOTES |
|---|---|
| Emission | All bodies will emit electromagnetic radiation in certain circumstances but the most efficient emission is from a ‘black body’ (see Sect. 5.4.3.1) |
| Reflection | Reflection of electromagnetic radiation is not possible for the higher energy radiations (X and gamma radiation) |
| Refraction | Refraction of electromagnetic radiation is not possible for the higher energy radiations (X and gamma radiation) |
| Transmission | Different materials are transparent to different wavelengths or photon energies |
| Attenuation | Different attenuation processes are possible depending on the photon energy of the radiation but, if the photons all have the same energy, the attenuation is always exponential. Photoelectric absorption can occur from ultraviolet to gamma radiations. Compton scattering is produced by X and gamma radiations. Pair production is an attenuation process which is possible if the photon energies are higher than 1.02 MeV |
| Luminescence – fluorescence and phosphorescence | Electron transitions within the material being irradiated cause the emission of photons that have less energy than the incident radiation. A single photon of incident radiation can produce many fluorescent photons |
As discussed in Chapter 16, there is a wave–particle duality which exists when electromagnetic radiation interacts with matter. This will be discussed further in the following sections.
17.3.1 Wave-like properties
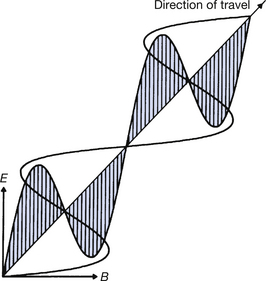
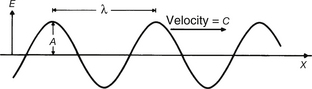
As the term electromagnetic suggests, electromagnetic radiation consists of both electric and magnetic fields. These fields are at right angles to each other and to the direction of propagation and are shown diagrammatically in Figure 17.1. As shown in E and B of the figure, both the electric and the magnetic vectors (see Sect. 4.3) vibrate transversely to the direction of propagation of the wave. In addition, the vectors vary in a sinusoidal manner, as shown in the figure. Thus, if we draw the variations of the electric vector (for example), a sine wave results, as shown in Figure 17.2. These periodic variations of the vectors are the reason why electromagnetic radiations are often referred to as electromagnetic waves and this was the sole method of explaining the behaviour of such radiations adopted by classical physics (see Sect. 16.6). The same parameters can be used to describe this type of wave formation as can be used for any sinusoidal waves. These are:
• the cycle– one complete waveform (this can start from any point on the wave and end at the corresponding point on another wave)
• the wavelength– the distance travelled in completing one cycle (λ)
• the frequency– the number of cycles per second (Hz)
• the amplitude– the magnitude of the peak of the wave above the x-axis (A).
If we consider Figure 17.2, it should be apparent that we can calculate the distance travelled by the radiation in 1 second by multiplying the wavelength (λ) by the frequency (v). However, the distance travelled in 1 second is simply the velocity of the radiation (c in a vacuum) and so we have:
in a vacuum.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree