Chapter 6 Electrostatics
Chapter contents
6.3 Properties of electrical charges 33
6.4 Force between two electrical charges in a vacuum 34
6.5 Permittivity and relative permittivity (dielectric constant) 35
6.6 Electrical field strength 35
6.7 Electrostatic induction of charge 35
6.9 Distribution of electrical charge on an irregulary shaped conductor 38
6.1 Aim
This chapter introduces the reader to the concepts involved in understanding the electrostatics which is relevant to radiographic science. This involves the consideration of electrical charge, charge distribution and electrical potential and potential difference.
6.3 Properties of electrical charges
The general properties of electrical charges are as follows:
• Charges can be considered as being of two types: positive and negative.
• The smallest unit of negative charge which can exist in isolation is that possessed by an electron, and the smallest unit of positive charge which can exist in isolation is that possessed by a proton.
• Electrical charges exert forces on each other even when they are separated by a vacuum. The forces are mutual, equal and opposite, as expected by Newton’s third law (see Sect. 3.5).
• Like charges (i.e. charges of the same sign) repel each other while unlike charges (of opposite signs) attract each other.
• The magnitude of the mutual forces between the charges is influenced by:
 the inverse square of the distance between the charged bodies – this is another application of the inverse square law (see Ch. 26).
the inverse square of the distance between the charged bodies – this is another application of the inverse square law (see Ch. 26).• Electrical charges may be induced in a body by the proximity of a charged body, leading to a force of attraction between the two bodies.
• Electrical charges may flow easily in some materials (called electrical conductors) and with difficulty in other materials (called electrical insulators). Both types of material are capable of having charges induced in them.
• When electrical charges move, they produce a magnetic field.
6.4 Force between two electrical charges in a vacuum
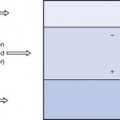
Consider two charges, q1 and q2, separated by a distance, d, in a vacuum, as shown in Figure 6.1.
Thus, F is proportional to the magnitude of each charge and to the inverse square of the distance separating them.
If we combine the factors in 1, 2 and 3 above, we can produce the equation:
If q1 and q2 both have the same sign, then F will be positive and will represent a force of repulsion. If the charges have opposite signs, then F will be negative and will represent a force of attraction.
If we wish to replace the proportionality sign in Equation 6.1 by an equals sign then we need to introduce a constant of proportionality (see Appendix A). This equation now reads:
This equation is often referred to as Coulomb’s law of force between two charges and has particular relevance when we consider the charges between subatomic particles (see Chs 18 and 19).


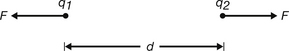
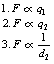
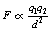
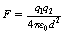
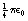 , where ε0 is the permittivity of a vacuum and has a value of 6.85 × 10−12 F.m−1. The charges q1, and q2 are expressed in coulombs, the separation d is in meters and the force F is in newtons.
, where ε0 is the permittivity of a vacuum and has a value of 6.85 × 10−12 F.m−1. The charges q1, and q2 are expressed in coulombs, the separation d is in meters and the force F is in newtons.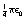 newton.
newton.