Element Simulations Explore a Novel Strategy for Surgical Repair of Congenital Aortic Valve Insufficiency

Fig. 1.

(A) Aortic valve leaflet shape is determined by averaging the leaflet outlines from 18 porcine hearts. (B) Left coronary (LC), noncoronary (NC), and right coronary (RC) leaflets are scaled to model a human valve with a congenitally undersized RC leaflet, and a mesh of unstructured triangles is generated within each of the three average leaflet outlines. The collagen fiber direction (principal material axis) is also shown. (C) The planar leaflet meshes are wrapped into a cylinder. Closure and loading of the valve is simulated in two steps. (D) First loads are applied to the mesh vertices that lie on the aortic root to simulate the radial and axial dilation of the aortic root in diastole. (E) Then surface normal forces are applied to all leaflet elements to simulate peak diastolic transleaflet pressure.

In simulating aortic valve repair strategies, our primary concern is whether the repaired valve will close without regurgitation under diastolic pressure load. We simulate the state of diastolic loading in two steps. First, loads are applied to the boundary points where the leaflet mesh meets the aortic root to simulate the state of radial and axial stresses in the aortic root in diastole, modeling the aortic root implicitly as an orthotropic cylinder with elastic moduli taken from the literature [6]. Then surface normal forces are applied to leaflet elements to simulate peak diastolic transleaflet pressure.

To simulate different strategies for resecting portions of the aortic root, we move the leaflet boundary points in order to achieve the modified aortic root shape prior to simulating valve closure. We are interested in the effect of resecting patches of various shapes from the aortic root adjacent to the NC leaflet: (1) a triangular patch oriented such that no material is removed at the level of the annulus (i.e., the nadir of the leaflet attachment) and the maximum is removed at the level where the tops of the leaflets attach (i.e., the commissures), (2) a rectangular patch where a strip of uniform width is resected from the level of the annulus to that of the commissures, (3) a triangular patch oriented such that no material is removed at the level of the commissures and the maximum is removed at the level of the annulus, and (4) a diamond-shaped patch where no material is removed at the level of the annulus or commissures and the maximum is removed at the level halfway between the two (Fig. 2). We refer to these resection shapes as TriUp, Rect, TriDown, and Diamond, respectively. Note that for the Rect and TriDown shapes, a portion of the valve annulus (where the leaflet attaches) is removed. In these cases, the NC leaflet meshes are modified to remove a triangular-shaped portion of the leaflet mesh that shares the resected annulus. The mesh is stitched back together by applying spring forces to approximate the cut edges during simulated resection and closure.

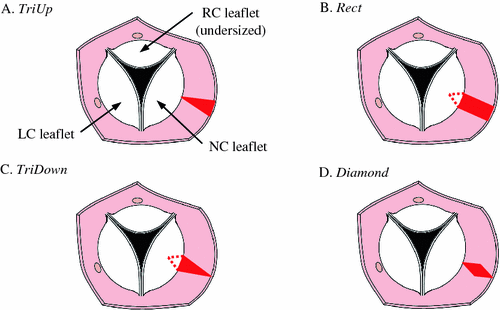
Fig. 2.

Drawing of transected aorta showing top view of the aortic valve. Four strategies are shown for resecting a portion (shown here in red) of the NC aortic root to try to compensate for an undersized RC leaflet: (A) triangular resection with base at the level of the commissures, (B) rectangular resection, (C) triangular resection with base at the level of the annulus, and (D) diamond-shaped resection.

A normal aortic valve is characterized by several millimeters of overlap (coaptation) between adjacent leaflets when closed, and it has been shown that achieving this redundancy following valve repair is associated with good long-term outcomes [12]. Accordingly, we determine the adequacy of simulated valve closure by computing the minimum extent of coaptation of adjacent leaflets in the closed state as well as the total area of coaptation for a given leaflet.

We simulate the equations of motion, including contact mechanics, and solve for the final deformed state of the valve using semi-implicit numerical integration with adaptive time-step control. All simulation and analysis software was written in the Matlab programming language (Mathworks, Natick, MA, USA). See our previous work for details of the modeling method [8].

3 Results

The simulated closed state for a valve with a congenitally undersized RC leaflet exhibited failure to close completely under typical diastolic transvalvular pressure of 80 mmHg (Fig. 3A). A map of the portion of the RC leaflet that coapts with the adjacent leaflets shows a large central portion of the RC leaflet that does not contact the other leaflets (Fig. 3B). For the five strategies for resection of the NC root that we simulated, only three (Rect5, Rect10, and TriDown) resulted in at least marginal central coaptation (Fig. 3B). Of those three, only the strategy of resecting a 10 mm wide rectangular section (Rect10) of the NC root resulted in a repair with sufficient central coaptation to be considered acceptable. This strategy also resulted in the repair with the largest total area of the RC leaflet involved in coaptation, and the results for total coaptation area generally echoed those for central coaptation height (Table 1).

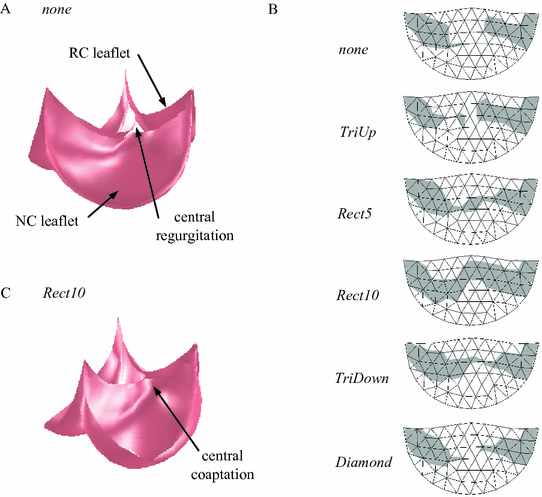
Fig. 3.

Simulation results showing (A) the closed, loaded state of the valve model representing the case of the pathological valve with no resection of the NC aortic root. Note the regurgitant orifice formed due to inability of the three leaflets to meet in the valve center. (B) The region of the RC leaflet that coapts with the other two leaflets (shaded gray) for various root resection shapes. Rect5 and Rect10 refer to the width of the resected rectangle in millimeters. The width of the triangle and diamond regions was approximately 10 mm. (C) The closed, loaded state of the valve model representing the Rect10 resection shape. Note the central coaptation where the three leaflets meet.

Only gold members can continue reading. Log In or Register to continue