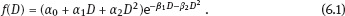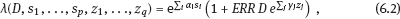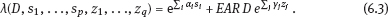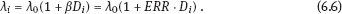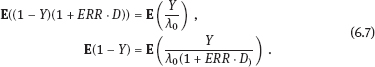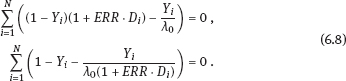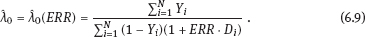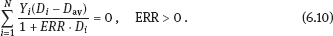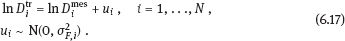6Estimation of radiation risk under classical or Berkson multiplicative error in exposure doses As well known, today the most common methods for estimation of radiation risks that associated with human exposure (Preston et al., 1993; Ron et al., 1995; Jacob et al., 2006; Likhtarov et al., 2006a; Tronko et al., 2006; Zablotska et al., 2011) use a number of principle approximations. In particular, the assumption of no uncertainty in individual dose, i.e., it is assumed that we have the determined value for the exposure dose of a subject. It is clear that such a statement is fundamentally wrong, since there are practically no situations in which being estimated by any method dose would not have some statistical distribution (Likhtarov et al., 2012, 2013a, 2014). One of the consequences from the assumption of the absence of errors in exposure doses is the bias of risk estimates and distortion of the shape of curve “dose–effect” (Carroll et al., 1995, 2006; Kukush et al., 2011; Masiuk et al., 2013, 2016). Note that such distortions of the risk estimates can be caused not only by systematic errors in dose estimates which is obvious, but by random errors as well. And although recently repeated attempts to include dose errors in the risk analysis have been made (Mallick et al., 2002; Kopecky et al., 2006; Lyon et al., 2006; Carroll et al., 2006; Li et al., 2007; Masiuk et al., 2008, 2011, and 2013; Little et al., 2014), the problem is not fully resolved until the present time. It is known that exposure doses estimation is inevitably accompanied by either the classical or Berkson type errors, or a combination of them (Mallick et al., 2002; Kopecky et al., 2006; Lyon et al., 2006; Li et al., 2007; Likhtarov et al., 2014, 2015; Masiuk et al., 2016). However, at the moment there is no final conclusion on the impact of the classical, Berkson, or mixed error in dose estimates to the final result of risk analysis, usually being expressed in values of either excess relative risk (ERR) or excess absolute risk (EAR); see Health risks from exposure to low levels of ionizing radiation (2006). One of the bright examples of importance of this problem is risk analysis of the results of long-term radio-epidemiology cohort studies of children with exposed thyroid due to the accident at Chornobyl nuclear power plant (Tronko et al., 2006; Bogdanova et al., 2015). It is vital to note that in the studies, absolute and relative frequencies of thyroid cancer in this cohort have been identified fairly. Not only point but also interval (in a statistical sense) doses estimates have been obtained (Likhtarov et al., 2005, 2006b, 2012, 2013a, 2014). However, due to the lack of a more or less acceptable mathematically grounded computational procedure for combining two-dimensional error in dose and effect within a single procedure of risk analysis, the risks estimation of radiation-induced effects was performed by the popular in radio-epidemiology computer package EPICURE (Preston et al., 1993). The latter operates with deterministic dose values and is not adapted to take into account any uncertainty of input data. Chapters 6 and 7 considers method taking into account both classical and Berkson errors in radiation doses for risk estimation in regression with binary response. The quality of the estimates is verified by means of stochastic simulation experiment for linear two-parameter risk model. As known (Health risks from exposure to low levels of ionizing radiation, 2006), at relatively low doses the risk of radiation-induced effect either depends on the dose linearly or contains both linear and quadratic term in dose. Radiobiological theory indicates that at low doses, the risk of a biological lesion being formed should depend linearly on dose if a single event is required or on the square of dose if two events are required. It is commonly held that high linear energy transfer radiation can cause lesions by the transversal of a single particle, and low linear energy transfer radiation does it by either one or two photons (or energetic beta particles). At higher doses of radiation, cell sterilization and cell death compete with the process of malignant transformation, thereby attenuating the risk of cancer at higher doses. The probability of cell death is subject to ordinary survival laws, i.e., it has a negative exponential dependence on the dose (or on squared dose). Combining these principles, one can get a general model for dependence of the radiation risk on the dose D that is widely used in radio-epidemiology for low linear energy transfer radiation: Here, α0, α1, α2, β1, and β2 are model parameters to be estimated from the data. The models for dependence on dose are generally incorporated into risk models by assuming that the excess risk functions are proportional to f (D), where the multiplicative constant (in dose) depends on such risk modifiers of radio-induction as sex and age at the moment of exposure. Moreover, for most malignant tumors (other than leukemia and bone cancer) the risk of disease increases over time of surveillance. Therefore, as a rule, most of risk estimates are based on the assumption that the risk increases during the life span of the population. The most radio-epidemiologic studies (Likhtarov et al., 2006a; Tronko et al., 2006; Zablotska et al., 2011; Little et al., 2014) use the following linear models for risk estimation: –relative risk model: –absolute risk model: Consider the two-parameter linear in dose regression model with binary response: where λi is the total risk or total incidence rate, or as a version with relative risk: Here Di is the individual exposure dose, λ0 is the background incidence rate (i.e., in the absence of the dose factor), β = ERR is excess relative risk, EAR = λ0β = λ0 ·ERR is excess absolute risk. In this instance, λ0 and EAR (or ERR) are positive model parameters to be estimated. The observed sample consists of couples (Yi, Di), i = 1,…, N, where Di are the doses (nonnegative numbers); Yi = 1 in the case of disease within some time interval, and Yi = 0 in the absence of disease within the interval. Model (6.4) resembles the logistic model (4.231) and (4.232), but the latter has total incidence rate being exponentially (not linearly) dependent on the dose: λi = exp(μ0+μ1Di). From relations (6.4)–(6.6) it follows that Replacing the expectations in (6.7) by the empirical means, we get the unbiased equation (see Appendix A1) for estimation of regression parameters λ0 and ERR : From the first equation (6.8) we have Excluding λ0 from system (6.8), we obtain a relation for the estimator of the parameter ERR: Here Dav is mean exposure dose for healthy subjects from the sample: In more detail, the properties of estimators (6.9) and (6.10) are studied in Appendix B. Compared to the maximum likelihood estimates (MLEs), the estimates (6.9) and (6.10) are efficiently computed because their evaluation is reduced to a nonlinear equation with one variable. As shown in the simulation study, the estimates (6.9) and (6.10) possess good asymptotic properties as the sample size increases. (This follows as well from a general theory of estimating equations (see Appendices A1 and A2).) Therefore, they can be used as initial approximation in computation of the MLE. Analyzing the impact of dose errors on the estimation of radiation risks, it is important to establish the essence mechanism of such errors. There are two basic models of the errors: the classical and Berkson ones (see Section 1.2). In practice, these two types of errors are usually realized jointly (Mallick et al., 2002; Masiuk et al., 2016). However, their impact on the radiation risk estimates cardinally differs. Therefore, it is advisable to consider the classical and Berkson errors separately from each other. As a rule, the errors in doses are multiplicative in their nature. Hence, we will consider both classical and Berkson errors regarding the logarithms of exposure doses. Let Dtr be the true value of exposure dose (usually Dtr is unknown), and Dmes be its measured value. If we have a multiplicative log-normal Berkson dose error, then Here, The variable wi can be either random or deterministic. If wi is random, then both wi and ui are assumed stochastically independent. In case of Berkson error, the conditional distribution of the logarithm xi of true dose is given as i.e., for each observation there is known the conditional distribution of the true random variable (i.e., of the logarithm of dose), but its exact realization is unknown (see Figure 6.1(a)). The Berkson error occurs every time when the dose mean value is applied instead of the dose true value. In particular, if the individual dose values are unknown, but approximated values of their expectations are known (e.g., mean group estimates of individual doses (Likhtarov et al., 2005, 2014) obtained by numerical Monte Carlo procedure), then replacement of the true doses by their approximate expectations leads to measurement errors of Berkson type. The Berkson error (unlike the classical error) possesses a convenient property that the use of doses with moderate Berkson errors in the linear (w.r.t. the dose) risk model practically does not bias the risk estimates (Carroll et al., 2006; Kukush et al., 2011; Masiuk et al. 2013, 2016). Let the dose be observed with the classical log-normally distributed multiplicative error. Then Here, In case of the classical error, From (6.15), it follows that the conditional distribution of the logarithm of measured dose wi has known variance and unknown expectation, which is regarded as the logarithm of true dose (see Figure 6.1(b)). The classical error occurs when the measured dose value (i.e., some computational and instrumental dose realization including the error) is used instead of the true dose value. For example, measurements of radioactivity and the results of questionnaires fluctuate just because of the presence of classical error. At first glance, it seems that the classical error stems out from the Berkson one by simply transferring the value ui to the right-hand side of (6.12): In view of the fact that ui and −ui are equally distributed, it seems that (6.16) is equivalent to (6.14). However, there is a significant difference: in (6.14), xi and ui are independent random variables, while in (6.16), wi and ui are independent. Therefore, the two error models (6.14) and (6.16) are quite different. Thus, in the presence of Berkson error the logarithm wi of measured dose is independent covariate, which characterizes the distribution of the logarithm of true dose, or more precisely, wi is its conditional expectation given the measured dose. On the other hand, in the presence of the classical error the logarithm wi of measured dose is a random variable correlated with the logarithm xi of true dose and the error ui. Berkson error compared with the classical error gives more information about the true dose. With Berkson error, at least we know the conditional distribution of the true dose (or of its logarithm xi). And with the classical error, we know only the logarithm of true dose up to the random error ui. Consider the full maximum likelihood (FML) method for the risk estimation in the presence of multiplicative error of Berkson type in exposure doses. Assume that in measured doses, only Berkson multiplicative error is present. Then
6.1General principles for construction of radiation risk models
6.2Linear two-parameter model
6.2.1Efficient estimators of parameters in linear model
6.3Two types of dose errors
6.3.1Berkson multiplicative error
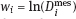 is the logarithm of measured doses (known quantity),
is the logarithm of measured doses (known quantity), 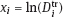 is the logarithm of true dose (unknown quantity), and ui is normal error with zero expectation and known variance
is the logarithm of true dose (unknown quantity), and ui is normal error with zero expectation and known variance 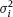 .
.
6.3.2The classical multiplicative error
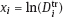 is unknown value of the logarithm of true dose,
is unknown value of the logarithm of true dose, 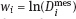 is known logarithm of the measured dose; ui is independent of xi normal random variable, with zero expectation and known variance (in other words ui is a random error).
is known logarithm of the measured dose; ui is independent of xi normal random variable, with zero expectation and known variance (in other words ui is a random error).
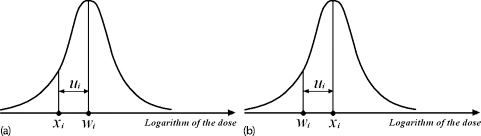
6.3.3Comparison of the classical and Berkson errors
6.4Methods of risk estimation in the models with Berkson multiplicative error in exposure dose
6.4.1Full maximum likelihood method
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree