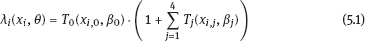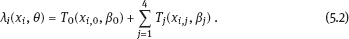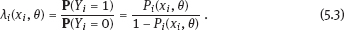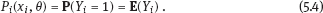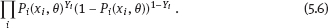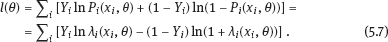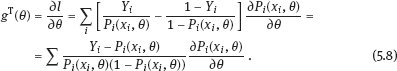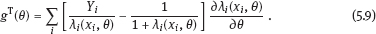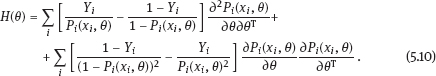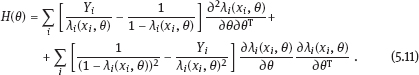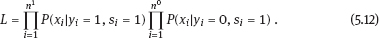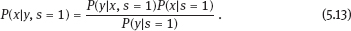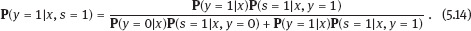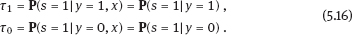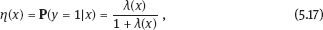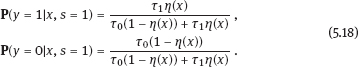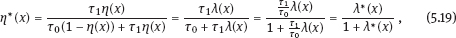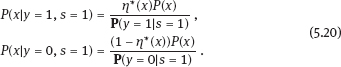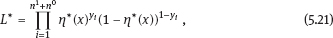Part II: Radiation risk estimation under uncertainty in exposure doses

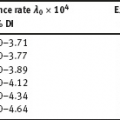
5Overview of risk models realized in program package EPICURE

EPICURE is a package of applied interactive computer programs designed on the base of original programs AMFIT and PYTAB, which were created by D. Preston and D. Pierce for the analysis of radiation effects in victims of the atomic bombing of Japanese cities Hiroshima and Nagasaki (Preston et al., 1993). The software package allows estimating parameters in generalized risk models and analyzing the data of epidemiological and experimental studies. EPICURE consists of four modules, each of which is designed for a particular type of data processing:

– binomial data (module GMBO ),

– matched data for the case-control study (module PECAN ),

– survival data (module PEANUTS ),

– grouped data that have Poisson distribution (module AMFIT ).

Each module of the software package includes statistical models to estimate the parameters of the generalized risk λi (xi, θ ), which is a function of the vector of covariates xi = {xi, 0, xi, 1,…, xi, 4} and the parameters θ = {β0, β 1,…, β4} of a regression model for observations with numbers i = 1, 2,… , n. Each of xi, 0, xi, 1 ,…, xi, 4 and β0, β1,…, β4 is a vector. Mathematical content of λi (xi, θ) depends on a type of statistical regression model. The content of each module in EPICURE is described as follows:

–GMBO – the binomial odds or a function of the odds,

–PECAN – the odds ratio for cases and controls,

–PEANUTS – the relative risk or hazard ratio modifying a nonparametric underlying hazard function for censored survival data,

–AMFIT – the Poisson mean or a piecewise constant hazard function for grouped survival data.

Formally, being programmed in EPICURE a regression model can be specified as the relative risk

or the absolute risk

Here T0(xi,0, β0) and Tj(xi,j, βj) are products of linear and log-linear functions of regression parameters.

5.1Risk analysis of individual data (GMBO module)

Mathematical basis of the software GMBO module is regression model with binary response Yi that takes two values, usually 0 and 1. The model is used typically if an epidemiologist has data of individual observations. This situation is common for cohort studies, the essence of which is that there is some group (cohort) of individuals exposed to radiation or other factor. Later on, some subjects of the cohort may get cancer disease, i.e., each subject of the cohort can be corresponded to a binary variable that takes the value 0 (“ith person is not diseased”) or 1 (“ith person is diseased”). It is assumed that the researcher has complete information on each individual from the cohort (i.e., the researcher knows his/her age, sex, individual dose, the implementation time of disease, time elapsed since exposure, age at exposure, etc.). Having data on each subject of the cohort and using one of the models of absolute or relative risk, it is possible to write down the risk of disease as 1.

Here Pi(xi, θ) is probability of 1, or expectation of Yi:

It is evident that

Further, based on these probabilities, one can construct the likelihood function, whose maximum point defines the estimate of the vector θ of unknown coefficients. The likelihood function for logistic model is given as a product (see Example 4.7):

Respectively, the log-likelihood function is equal to

The gradient of the log-likelihood function is given by the equality

Using (5.5), transforming (5.8):

The Hessian matrix is given as

Expressing Pi (xi, θ) via the function λi(xi, θ ), we get

Having expressions for the gradient and Hessian, one can maximize the function l(θ) using the Newton–Raphson numerical method or another optimization method.

5.2Case-control study (PECAN module)

The PECAN module is designed for data processing of epidemiological case-control studies. In contrast to cohort studies, the binary outcome variable in a case-control study is fixed by stratification. The dependent variables in this setting are one or more primary covariates, exposure variables in x. In this type of study design, samples of fixed size are chosen from the two strata defined by the outcome variable. The values of the primary exposure variables and the relevant covariates are then measured for each subject selected. At this, the main covariate (dose) and other significant covariates (such as gender, age, etc.) are assumed known. The total likelihood function is the product of stratum-specific likelihood functions, which are dependent on the probability of getting a subject to the sample with given distribution of covariates. After some simple transformations, one can obtain the logistic (or similar to logistic) regression model, where the response variable will be in reality interesting for a researcher (Hosmer et al., 2013). A key point of the mentioned transformations is Bayes’ theorem.

Let a variable s mean selection (s = 1) or not selection (s = 0) of a subject. The likelihood function for a sample of n1 cases (subjects with realization of the effect y = 1) and n0 controls (subjects without realization of the effect y = 0) can be written follows:

After applying Bayes’ theorem to the individual probabilities from (5.12), we get

Applying Bayes’ theorem to the first factor in the numerator of (5.13) for y = 1, we have

Similarly for y = 0,

Suppose that the selection of cases and controls is independent from covariates that influence the disease incidence, i.e., from the vector x. Denote the probability of selection of the case and control by τ1 and τ0, respectively, i.e.,

Denote by η (x) the conditional probability of the case:

where λ (x) is the total incidence rate.

Substituting (5.16) and (5.17) to (5.14) and (5.15), we obtain

Introduce a notation

with .

Substituting (5.18) with the notation (5.19) to (5.13) and bearing in mind that the selection of cases and controls is independent of x, weget

If we denote

then the likelihood function (5.12) is written as

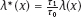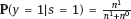The first factor L∗ on the right-hand side of (5.22) is constructed in the same manner as the likelihood function for cohort studies, but by the data obtained within the case-control study. If the distribution of covariate P (xi) does not depend on the model parameters, and the selection of cases and controls is carried out randomly from the same subset, i.e., the conditions and 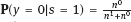hold true, then the likelihood function L∗ can be used for the risk coefficients estimation.