used to describe the region of interest D consists of four elements, namely, a probabilistic atlas (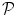 ), texture-based features (
), texture-based features (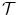 ), relationships
), relationships 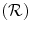 , and specific segmentation methods
, and specific segmentation methods 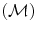 for organs in the region D,
for organs in the region D, 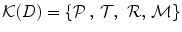 . We construct a probabilistic atlas
. We construct a probabilistic atlas 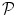 for our data D, which is a map that assigns to each voxel a set of probabilities to belong to each of the organs,
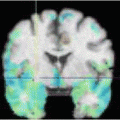
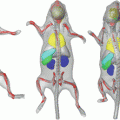
for our data D, which is a map that assigns to each voxel a set of probabilities to belong to each of the organs, 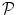 (D) = (p 0, p 1, p 2, . . . , p N ), where p i is the probability for the voxel to belong to organ i, (1 ≤ i ≤ N). All the organs other than those that are manually delineated are assigned the probability p 0 where p 0 = 1–Σ k = 1 N pk. The probabilistic atlas is constructed in the training phase of the frame-work. We initialize the organs present in the atlas during deployment using registration techniques described in [15]. This helps us to gain insight on the spatial information of different organs and variations with respect to one another, and also guides automated segmentation procedures.
(D) = (p 0, p 1, p 2, . . . , p N ), where p i is the probability for the voxel to belong to organ i, (1 ≤ i ≤ N). All the organs other than those that are manually delineated are assigned the probability p 0 where p 0 = 1–Σ k = 1 N pk. The probabilistic atlas is constructed in the training phase of the frame-work. We initialize the organs present in the atlas during deployment using registration techniques described in [15]. This helps us to gain insight on the spatial information of different organs and variations with respect to one another, and also guides automated segmentation procedures.
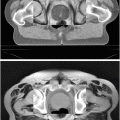
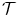 = {T 1, T 2, . . . , T N }, where T i = [f 1 i , f 2 i , …, f k i ] is set of optimal texture-based features selected in the training phase for discrimination for organ i, (1 ≤ i ≤ N) and k is the number of features for organ i. The optimal texture-based features are selected in the training phase of our framework. Texture-based features are used by the image analysis methods to segment the organs and refine the initialization by the probabilistic atlas.
= {T 1, T 2, . . . , T N }, where T i = [f 1 i , f 2 i , …, f k i ] is set of optimal texture-based features selected in the training phase for discrimination for organ i, (1 ≤ i ≤ N) and k is the number of features for organ i. The optimal texture-based features are selected in the training phase of our framework. Texture-based features are used by the image analysis methods to segment the organs and refine the initialization by the probabilistic atlas.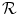 = {R r,t |r, t organs}, where R r,t ∈ {posterior, anterior, right, left, child, parent}, r is the reference organ and t is the target organ. For example, R i,j = child means that, the reference organ i (e.g., ventricle) is the child of the target organ j (e.g., heart); while R i,j = right implies that the reference organ i (e.g., right lung) is to the right of the target organ j (e.g., heart).
= {R r,t |r, t organs}, where R r,t ∈ {posterior, anterior, right, left, child, parent}, r is the reference organ and t is the target organ. For example, R i,j = child means that, the reference organ i (e.g., ventricle) is the child of the target organ j (e.g., heart); while R i,j = right implies that the reference organ i (e.g., right lung) is to the right of the target organ j (e.g., heart).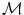 = {M 1, M 2, . . . ,M K }. Due to high anatomic variations and the large amount of structural information found in medical images, global information based segmentation methods yield inadequate results in region extraction. We use the knowledge-based atlas to guide the automatic segmentation process and then use specific image analysis methods for segmentation of anatomical structures. We examine the performance of these methods in the training phase and accordingly select methods with higher accuracy and true positive rate as well as lower false positive rate. One of the segmentation methods used is the multi-class multi-feature fuzzy connectedness method, which is described in the following section.
= {M 1, M 2, . . . ,M K }. Due to high anatomic variations and the large amount of structural information found in medical images, global information based segmentation methods yield inadequate results in region extraction. We use the knowledge-based atlas to guide the automatic segmentation process and then use specific image analysis methods for segmentation of anatomical structures. We examine the performance of these methods in the training phase and accordingly select methods with higher accuracy and true positive rate as well as lower false positive rate. One of the segmentation methods used is the multi-class multi-feature fuzzy connectedness method, which is described in the following section.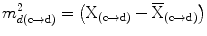 T
T 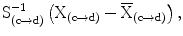 where
where 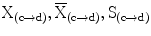 are the feature vector, the mean feature vector, and the covariance matrix in the direction from c to d, respectively. The bias in intensity in a specific direction is accounted for by allowing different levels and signs of intensity homogeneities in different directions of adjacency [13]. Thus, this formulation accounts for different levels of the increase or decrease in intensity values in the horizontal (left, right) or vertical (up, down) directions. The advantage of using the Maha-lanobis metric is that it weighs the differences in various feature dimensions by the range of variability in the direction of the feature dimension. These distances are computed in units of standard deviation from the mean. This allows us to assign a statistical probability to the measurement. The local fuzzy spel affinity is computed as: μ κ (c, d) =
are the feature vector, the mean feature vector, and the covariance matrix in the direction from c to d, respectively. The bias in intensity in a specific direction is accounted for by allowing different levels and signs of intensity homogeneities in different directions of adjacency [13]. Thus, this formulation accounts for different levels of the increase or decrease in intensity values in the horizontal (left, right) or vertical (up, down) directions. The advantage of using the Maha-lanobis metric is that it weighs the differences in various feature dimensions by the range of variability in the direction of the feature dimension. These distances are computed in units of standard deviation from the mean. This allows us to assign a statistical probability to the measurement. The local fuzzy spel affinity is computed as: μ κ (c, d) = 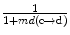 in order to ensure that μ κ (c, d) ∈ Z 2 → [0, 1] and it is reflexive and symmetric, where Z 2 is a set of all pixels of a two-dimensional Euclidean space.
in order to ensure that μ κ (c, d) ∈ Z 2 → [0, 1] and it is reflexive and symmetric, where Z 2 is a set of all pixels of a two-dimensional Euclidean space.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree