Internal Radiation Dosimetry



(14.1)



It should be noted that the roentgen applies only to air and to x- or γ-radiations. Because of practical limitations of the measuring instruments, the R unit is applicable only to photons of less than 3 MeV energy.

The rad is a more universal unit. It is a measure of the energy deposited per unit mass of any material by any type of radiation. The rad is specifically defined as




$$ {1}\;{\text{rad}} = {1}00\;{\text{ergs/g}}\;{\text{absorber}} $$

(14.2)

Since 1 joule (J) = 107 ergs,




$$ {1}\;{\text{rad}} = {1}{0^{ - {2}}}\;{\text{J/kg}} $$

(14.3)

Another radiation unit is kerma (acronym for kinetic energy released in matter) which is defined as the sum of initial kinetic energies of all charged particles liberated by uncharged ionizing radiation per unit mass of material. For all practical purposes, kerma and rad are identical.

In SI units , the gray (Gy) is the unit of radiation absorbed dose and kerma and is given by




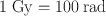
$$ {1}\;{\text{Gy}} = {1}00\;{\text{rad}} $$

(14.4)




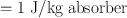
$$= {1}\;{\text{J}}/{\text{kg}}\;{\text{absorber}} $$

(14.5)

It can be shown that the energy absorbed per kilogram of air due to an exposure of 1 R is




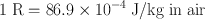
$$ {1}\;{\text{R}} = {86.9} \times {1}{0^{ - {4}}}\;{\text{J/kg in air}} $$

Therefore,




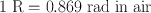
$$ {1}\;{\text{R}} = 0.869\;{\text{rad in air}} $$

or,




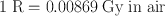
$$ {1}\;{\text{R}} = 0.00869\;{\text{Gy in air}} $$




$$ \begin{aligned} {\text{Note that for soft tissue,}}\;{\text{1R}} & = 0.96\;{\text{rad}} \\ & = 0.0096\;{\text{Gy}} \end{aligned} $$

The rad is not restricted by the type of radiation or absorber or by the energy or intensity of the radiation. It should be understood that the rad is independent of the weight of the material. This means that a radiation dose of 1 rad (0.01 Gy) is always 1 rad (0.01 Gy) in 1, 2, or 10 g of the material. However, the integral absorbed dose is given in units of gram-rad (g · rad or g · Gy) and calculated by multiplying the rad (Gy) by the mass of material. For example, if the radiation dose to a body of 45 g is 10 rad (0.1 Gy), then the integral radiation dose to the material is 450 g · rad (or 4.5 g · Gy); however, the radiation dose is still 10 rad (0.1 Gy).

The dose equivalent unit, rem, has been developed to account for the differences in effectiveness of different types of radiation in causing biological damage. In radiobiology, the rem is defined as




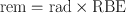
$$ {\text{rem}} = {\text{rad}} \times {\text{RBE}} $$

(14.6)

where RBE is the relative biological effectiveness of the radiation. It is defined as the ratio of the dose of a standard radiation to produce a particular biological response to the dose of the radiation in question to produce the same biological response. Radiations of 250 KV x-rays are normally chosen as the standard radiation because of their widespread use. RBE varies with the linear energy transfer (LET) of the radiation , radiation dose, dose rate , and the biological system in which RBE is determined.

In radiation protection, RBE is replaced by the radiation weighting factor , W r , to account for differences in effectiveness of various radiations in causing biological damage . The rem is then defined as




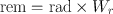
$$ {\text{rem}} = {\text{rad}} \times {W_r} $$

(14.7)

The International Commission on Radiological Protection (ICRP) has suggested the W r values for different radiations, which are listed in Table 14.1 (ICRP 60 1991). These values depend on the LET of the radiation. When a radiation dose comes from several radiations, the total dose equivalent is calculated by adding the absorbed doses from individual radiations multiplied by the W r of each radiation.


Table 14.1
Radiation weighting factors







































Type and energy range
Radiation weighting factors (W r )

Photons, all energies
1

Electrons, muons, all energies
1

Neutrons, energy
< 10 keV
5

10 to 100 keV
10

 > 100 to 2 MeV
20

> 2 to 20 MeV
10

> 20 MeV
5

Protons, other than recoil protons, energy > 2 MeV
5

Alpha particles, fission fragments, heavy nuclei
20


Adapted with permission from ICRP Publication 60: 1990 Recommendations of the international commission on radiological protection. New York: Pergamon Press; 1991.

In the past, the W r values were called quality factors , which are somewhat different from the W r values. The US Nuclear Regulatory Commission (NRC) still adopts these values for regulatory purposes, and the values are listed in Table 14.2.


Table 14.2
Quality factors for different radiations






















Type of radiation
QF

X-rays, γ-rays, β-particles
1.0

Neutrons and protons
10.0

α-Particles
20.0

Heavy ions
20.0

In SI units, the dose equivalent is expressed in sievert , which is defined as




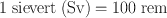
$$ {1}\;{\text{sievert}}\;(\text{Sv}) = {1}00\;{\text{rem}} $$

(14.8)

In practical situations, all these radiation units are often expressed in milliroentgens (mR), millirads (mrad), and millirems (mrem), which are 10−3 times the units, roentgen, rad, and rem, respectively. In SI units, the equivalent quantities are milligrays (mGy) and millisieverts (mSv). A rad is also commonly expressed as centigray (cGy), one-hundredth of a gray.



Dose Calculation


The radiation absorbed dose depends on a number of factors: (1) the amount of radioactivity administered; (2) the physical and biological half-lives of the radioactivity; (3) the fractional abundance of the radiation in question from the radionuclides; (4) the biodistribution of radioactivity in the body; and (5) the fraction of energy released from the source organ that is absorbed in the target volume, which is related to the shape, composition, and location of the target. The physical characteristics of a radionuclide are well established. Information concerning the biodistribution of ingested radioactivity can be obtained from various experimental studies in humans and animals. The factors four and five are variable from one individual to another and, therefore, they are approximated for a “standard” or “average” 70-kg man.

Radiopharmaceuticals administered to patients are distributed in different regions of the body. A region of interest for which the absorbed dose is to be calculated is considered the “target,” whereas all other regions contributing to the radiation dose to the target are considered “sources.” The source and the target become the same when the radiation dose due to the radioactivity in the target itself is calculated.


Radiation Dose Rate


Suppose a source volume r contains A µCi of a radiopharmaceutical emitting several radiations . If the ith radiation has energy E i and a fractional abundance N i per disintegration, then the energy absorbed per hour (dose rate ) by a target of mass m and volume v from the ith radiation emitted by the source volume r is given by




$$ \begin{aligned} {R_i}({\text{rad/h}}) & = A/m({\upmu {\text{Ci}}/{\text{g}}}){N_i}{E_i}({\text{MeV/disintegration}}) \\ &\; \times \left[{{3}.{7} \times {1}{0^{4}}\;{\text{disintegrations}}/({{\text{s}}\cdot\upmu {\text{Ci}}})}\right] \\ & \;\times ({{1}.{6} \times {1}{0^{ -6} }\;{\text{erg}}/{\text{MeV}}}) \\ & \; \times ({0.0{1}\;{\text{g}}\cdot{\text{rad}}/{\text{erg}}}) \\ & \; \times ({{\text{36}}00\;{\text{s}}/{\text{h}}}) \\ & = {2}.{\text{13}}({A/m}){N_i}{E_i} \end{aligned} $$

The above equation is valid for nonpenetrating radiations only, meaning all energy is absorbed in the absorber. For penetrating radiations , total or part of the radiation energy may be absorbed in the absorbing material. If the target and the source are not the same, then a factor must be introduced to account for the partial absorption, if any, of the radiation energy. Thus,




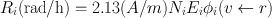
$$ {R_i}({\text{rad}}/{\text{h}}) = {2}.{\text{13}}({A/m}){N_i}{E_i}{\phi _i}({v \leftarrow r}) $$

(14.9)

Here ϕ i (v ← r) is called the absorbed fraction and is defined as the ratio of the energy absorbed by the target volume v from the ith radiation to the energy emitted by the ith radiation from the source volume r. This is a critical factor that is difficult to evaluate, because the absorbed fraction ϕ i depends on the type and energy of the radiation, the shape and size of the source volume, and the shape, composition, and distance of the target volume. However, in the case of β-particles, conversion electrons , α-particles, and x- and γ-rays of energies less than 11 keV, all of the energy emitted by a radionuclide is absorbed in the volume r larger than 1 cm. Then, ϕ i becomes 0, unless v and r are the same, in which case ϕ i  = 1. For x- and γ-rays with energies greater than 11 keV, the value of ϕ i decreases with increasing energy and varies between 0 and 1, depending on the energy. The values of ϕ i are calculated by statistical Monte Carlo methods on the basis of fundamental mechanisms of interaction of radiation with matter, and are available in standard textbooks on radiation dosimetry, particularly the medical internal radiation dose (MIRD) pamphlets published by the Society of Nuclear Medicine.

The quantity 2.13N i E i is a constant for the ith radiation and is often denoted by Δ i . Thus,




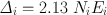
$$ {\mathit\Delta _i} = {2}.{\text{13}}\;{N_i}{E_i} $$

(14.10)

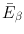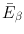The quantity Δ i is called the equilibrium dose constant for the ith radiation and has the unit g · rad/(µCi · h) based on the units chosen in Eq. (14.9). It should be pointed out that since β-particles are emitted with a distribution of energy, the average energy $$ \bar{E}_\beta $$ of β-particles, which is equal to one-third of Emax of the particle, is used in the calculation of Δ i . Thus, Eq. (14.9) becomes




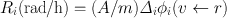
$$ {R_i}({\text{rad/h}}) = ({A/m}){\mathit\Delta _i}{\phi _i}({v \leftarrow r}) $$

(14.11)

The activity A will change due to the physical decay and biological elimination of the radiopharmaceutical, and therefore the dose rate will also change. If A o is the initial administered activity, then the activity localized in an organ is a fraction f of A o . Assuming an effective exponential change in A with time, Eq. (14.11) can be written as




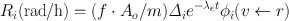
$$ {R_i}{\text{(rad/h)}} = (f\cdot{A_o}/m){\mathit\Delta _i}{e^{ - {\lambda _e}t}}{\phi _i}(v \leftarrow r) $$

(14.12)

Here λ e is the effective decay constant of the radiopharmaceutical, and t is the time over which the original activity has decayed.


Cumulative Radiation Dose


The cumulative radiation dose D i to the target due to the ith radiation of the radionuclide during the period t = 0 to t can be obtained by integrating Eq. (14.12). Thus,




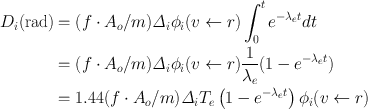
$$ \begin{aligned} {D_i}{\text{(rad)}} & = ({f\cdot{A_o}/m}){\mathit\Delta_i}{\phi _i}(v \leftarrow r)\int_0^t {{e^{ - {\lambda _e}t}}dt}\\ &= ({f\cdot{A_o}/m}){\mathit\Delta _i}{\phi _i}(v \leftarrow r)\frac{1}{{{\lambda _e}}}({1 - {e^{ - {\lambda _e}t}}}) \\ &= 1.44({f\cdot{A_o}/m}){\mathit\Delta _i}{T_e}\left({1 - {e^{ - {\lambda_e}t}}}\right){\phi _i}(v \leftarrow r) \end{aligned} $$

(14.13)

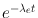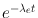Here, T e is the effective half-life of the radiopharmaceutical in hours (discussed in Chap. 3). If t = ∞, that is, the radiopharmaceutical is completely eliminated, then the exponential term $${e^{ - {\lambda _e}t}}$$ approaches zero and the absorbed dose in Eq. (14.13) may be written as




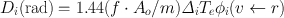
$$ {D_i}({\text{rad}}) = {1}.{\text{44}}({f\cdot{A_o}/m}){\mathit\Delta _i}{T_e}{\phi _i}({v \leftarrow r}) $$

(14.14)

If the radionuclide has n radiations with energies E 1, E 2,… E n and fractional abundances N 1, N 2,… N n per disintegration, then the total dose D can be obtained by summing Eq. (14.14) over all radiations. Thus,




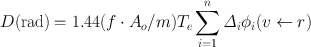
$$ D{\text{(rad)}} = 1.44({f\cdot{A_o}/m}){T_e}\sum\limits_{i = 1}^n {{\mathit\Delta _i}{\phi _i}(v \leftarrow r)}$$

(14.15)

This summation can also be applied to Eq. (14.12) for the dose rate R i . The total dose to the target from different sources of radiations can be calculated by summing Eq. (14.15) over all sources.

In the MIRD pamphlets, the values of Δ i have been compiled on the basis of various nuclear characteristics of the radionuclide in question. The ϕ i values have been calculated on the basis of different sizes and compositions of the targets receiving the radiation dose and the radiation characteristics of the radionuclide. In MIRD pamphlet no. 11, Eq. (14.15) has been substituted by




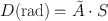
$$ D({\text{rad}}) = {\tilde A}\cdot S $$

(14.16)

where




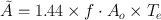
$$ {\tilde A} = {1}.{\text{44}} \times f\cdot{A_o} \times {T_e} $$

(14.17)




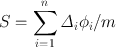
$$ S = \sum\limits_{i = 1}^n {{\mathit\Delta _i}{\phi _i}/m}$$

(14.18)

The quantity à is called the cumulated activity and has the unit of µCi · h. The quantity S is called the mean absorbed dose per cumulated activity and has the unit of rad/µCi · h. These two quantities are further discussed next.


Factors Affecting Ã


The cumulated activity à in Eq. (14.17) is given as




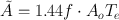
$$ {\tilde A} = {1}.{\text{44}}f\cdot{A_o}{T_e} $$

This is calculated on the assumption that the radiopharmaceutical localizes in the organs instantaneously and cleared by both physical decay and biological elimination.

There are situations when the uptake of the tracer is gradual and the clearance also is slow. In these cases,




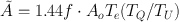
$$ {\tilde A} = {1}.{\text{44}}f\cdot{A_o}{T_e}({{T_Q}/{T_U}}) $$

(14.19)

where T U is the biological uptake half-time, T e is the effective excretion halftime (Eq. 3.12) and T Q is the effective uptake half-time. T Q is calculated by Eq. (3.12) using the physical half-life T P and the biological uptake halftime T U .

Two other situations can occur when the uptake is instantaneous, but the T P of the radionuclide is greater than the biological half-life T B , or T B is greater than T P .

When T P  >> T B , the cumulated activity is given by




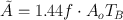
$$ {\tilde A} = {1}.{\text{44}}f\cdot{A_o}{T_B} $$

(14.20)

If the tracer is excreted by several excretion routes such as urinary excretion, fecal excretion, etc., the fraction of activity excreted and the effective halftime of each mode are used to calculate the fractional cumulated activity of each mode, which are then summed to calculate the total cumulated activity.

When T B  >> T P , the cumulated activity is calculated as




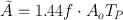
$$ {\tilde A} = {1}.{\text{44}}f\cdot{A_o}{T_P} $$

(14.21)

In this case, there is no biological excretion.


The S Values


The mean absorbed dose per cumulated activity , S, is more appropriately expressed as




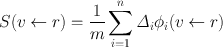
$$ S(v \leftarrow r) = \frac{1}{m}\sum\limits_{i = 1}^n {{\mathit\Delta _i}{\phi _i}(v \leftarrow r)}$$

(14.22)

where the symbols v and r represent the target and the source, respectively . The calculation of these values is quite laborious. The MIRD Committee of the Society of Nuclear Medicine calculates these values for radiopharmaceuticals commonly used in nuclear medicine and publish them periodically. Table 14.3 includes a partial list of S values for 99mTc obtained from MIRD pamphlet no. 11.


Table 14.3
S a, mean absorbed dose per unit cumulated activity (rad/µCi · h)b for 99mTc.















































































































































































































 
Source organs

Target organs
Bladder content
Stomach content
Kidneys
Liver
Lungs
Ovaries
Red marrow
Spleen
Testes
Thyroid
Total body

Adrenals
1.5E-07
2.7E-06
1.1E-05
4.5E-06
2.7E-06
3.3E-07
2.3E-06
6.3E-06
3.2E-08
1.3E-07
2.3E-06

Bladder wall
1.6E-04
2.7E-07
2.8E-07
1.6E-07
3.6E-08
7.2E-06
9.9E-07
1.2E-07
4.8E-06
2.1E-09
2.3E-06

Bone (total)
9.2E-07
9.0E-07
1.4E-06
1.1E-06
1.5E-06
1.5E-06
4.0E-06
1.1E-06
9.2E-07
1.0E-06
2.5E-06

Stomach
2.7E-07
1.3E-04
3.6E-06
1.9E-06
1.8E-06
8.1E-07
9.5E-07
1.0E-05
3.2E-08
4.5E-08
2.2E-06

Kidneys
2.6E-07
3.5E-06
1.9E-04
3.9E-06
8.4E-07
9.2E-07
2.2E-06
9.1E-06
4.0E-08
3.4E-08
2.2E-06

Liver
1.7E-07
2.0E-06
3.9E-06
4.6E-05
2.5E-06
5.4E-07
9.2E-07
9.8E-07
3.1E-08
9.3E-08
2.2E-06

Lungs
2.4E-08
1.7E-06
8.5E-07
2.5E-06
5.2E-05
6.0E-08
1.2E-06
2.3E-06
6.6E-09
9.4E-07
2.0E-06

Marrow (red)
2.2E-06
1.6E-06
3.8E-06
1.6E-06
1.9E-06
5.5E-06
3.1E-05
1.7E-06
7.3E-07
1.1E-06
2.9E-06

Ovaries
7.3E-06
5.0E-07
1.1E-06
4.5E-07
9.4E-08
4.2E-03
3.2E-06
4.0E-07
0.0
4.9E-09
2.4E-06

Skin
5.5E-07
4.4E-07
5.3E-07
4.9E-07
5.3E-07
4.1E-07
5.9E-07
4.7E-07
1.4E-06
7.3E-07
1.3E-06

Spleen
6.6E-07
1.0E-05
8.6E-06
9.2E-07
2.3E-06
4.9E-07
9.2E-07
3.3E-04
1.7E-08
1.1E-07
2.2E-06

Testes
4.7E-06
5.1E-08
8.8E-08
6.2E-08
7.9E-09
0.0
4.5E-07
4.8E-08
1.4E-03
5.0E-10
1.7E-06

Thyroid
2.1E-09
8.7E-08
4.8E-08
1.5E-07
9.2E-07
4.9E-09
6.8E-07
8.7E-08
5.0E-10
2.3E-03
1.5E-06

Total body
1.9E-06
1.9E-06
2.2E-06
2.2E-06

Only gold members can continue reading. Log In or Register to continue

Related posts:

Radiation Regulations and Protection Gas-Filled Detectors Structure of Matter Scintillation and Semiconductor Detectors Performance Parameters of Gamma Cameras Production of Radionuclides

Stay updated, free articles. Join our Telegram channel
Tags:
Aug 27, 2016 | Posted by in NUCLEAR MEDICINE | Comments Off on Internal Radiation Dosimetry

Full access? Get Clinical Tree

 Get Clinical Tree app for offline access