, Abas Sabouni2, Travis Desell3 and Ali Ashtari4
(1)
Department of Electrical Engineering, University of North Dakota, Grand Forks, ND, USA
(2)
Department of Electrical Engineering, Wilkes University, Wilkes-Barre, PA, USA
(3)
Department of Computer Science, University of North Dakota, Grand Forks, ND, USA
(4)
Invenia Technical Computing, Winnipeg, MB, Canada
Abstract
In this chapter a review of different electromagnetic (EM) imaging methods is presented. The focus on microwave tomography, the types, and advantages and disadvantages of local and global optimization in microwave imaging are reviewed.
1.1 Electromagnetic Imaging
Electromagnetic imaging, by means of radio frequency (RF), microwave, or optical signals, was always attractive due to its unique features as a diagnosis tool. Electromagnetic imaging has received intense attention, and therefore, extensive research has been conducted. This is due to the versatility and suitability of this imaging technique for a wide range of applications. For example, in the nondestructive evaluation (NDE), microwave imaging (MWI) has been proposed for online testing of material, in particular, the detection of possible defects and measurements of physical quantities (e.g., moisture content) on conveyed products [1–3]. It also can be used for material characterization, such as the determination of constituent, evaluation of porosity, and assessment of the curing state. In military applications, microwaves’ ability to penetrate into dielectric materials makes them useful for interrogating military composites [4–6]. In aerospace application, MWI may be useful for the detection of cracks that may occur in aircraft fuselage [7]. In the geographical prospecting field, MWI has been used in remote detection of subsurface inclusions such as tunnels, landfill debris, and unexploded land mines [8–10]. In civil and industrial engineering application, MWI can be useful for evaluating the structural integrity of roadways, buildings, and bridges [11]. In medicine, currently, MWI systems have been proposed for noninvasive biological imaging applications [12, 13]. Significant progress in MWI has been accomplished in the last decade, with experimental prototypes capable of imaging excised pig’s legs [14], heart disease such as ischemia and infraction [15–17], breast cancer imaging [18–30], brain imaging [31], bone imaging [32], and detecting ischemia in different parts of the body [33]. A general review of different biomedical applications of MWI can be found in [12]. Furthermore, the applications of microwave techniques to medical imaging have been summarized in [34]. The abovementioned examples are just a few of the electromagnetic imaging applications. One can imagine many other possible applications as long as there is enough penetration inside the target.
From this very short and incomplete list, it is apparent that the scope of electromagnetic imaging is extensive and applications can be found in many diverse fields. Some of these applications only require qualitative information about the object under test, whereas in many other cases, such as demining application, noninvasive archaeological survey, or medical imaging, there is a need for quantitative description of the scatterer such as its permittivity, velocity, and conductivity profiles. The quantitative information is obtainable from electromagnetic imaging by solving an inverse scattering problem. In inverse scattering, one attempts to infer the object from the field perturbation or the scattered field induced by the presence of the object. The inverse scattering problem is often quite difficult, especially when wave interactions are present, like the case of electromagnetic inverse scattering. It is usually nonlinear due to the multiple scattering effects within the scatterer and is often nonunique because the high-spatial-frequency portions of the object give rise to evanescent waves.
Many methods have been proposed in the past to solve particular classes of inverse scattering problems by making certain underlying assumptions about the object and the scattering process. In computed tomography (CT), for example, a ray picture is used whereby it is assumed that waves propagate in straight lines and all diffraction and multiple scattering effects are ignored. Diffraction tomography takes into account the diffraction, but ignores the multiple scattering effect and assumes that the object contrast is small.
1.2 Microwave Imaging Methods
Current research in MWI can be divided mainly into radar imaging and microwave tomography (MWT). In the MWT image reconstruction, a nonlinear inverse scattering problem must be solved to predict a map of the dielectric properties of the target. In this technique, the scattered field is measured at the observation points outside the object of interest, while in the radar approach, a simpler computational problem (linear inverse problem) is considered.
1.2.1 Radar Approach
Radar approaches can provide an image of the location of contrasts in the imaging medium. It cannot retrieve the values of dielectric properties. In this method of imaging, the transmitter antenna (TX) irradiates an electromagnetic waveform into the scan area. A contrast in the dielectric properties of the propagating media produces scattered fields, and the magnitude and phase of backscattered signals from the object of interest (OI) are then recorded by receiver antennas (RX). The scan can be in a circular or rectangular path. This method involves analyzing reflections from the OI to identify the presence of target.
Synthetic aperture radar (SAR) is a signal processing technique which reconstructs the contrast between the dielectric properties of the media. The reconstruction is based on measuring the scattered field in different locations which mimics the use of a very large antenna. SAR is based on measuring the phase shift of the reflected signal. The amplitude of the reflected wave is not involved in classical SAR signal processing. The reason is that amplitude attenuation depends on factors such as radar cross section, the distance between the antennas and the target, and electromagnetic loss in the media. It cannot be distinguished in the receiver end how much each factor has affected the amplitude. Therefore, amplitude information is not used in the reconstruction process.
On the other hand, time delays (phase shifts) in the receiver give information on the location of a contrast in dielectric properties in the media assuming that the propagation speed in the media is known and constant. In contrast to nonlinear methods, the SAR approach seeks only to identify the presence and location of strong scatterers rather than attempting to completely reconstruct the dielectric property profile.
Confocal microwave imaging (CMI) approach is one example of an SAR technique that uses the measured reflected signals to infer the locations of significant microwave scatterers. For example in breast cancer detection, scattering arises from significant contrasts in dielectric properties between normal breast tissue and malignant lesions [35]. CMI involves illuminating the breast with an ultra-wideband pulse from a number of physical antenna locations. The relative arrival times of the backscattered signal provide information that is used to determine the scatterer location using simple, robust synthetic focusing techniques.
SAR is relatively fast because it is not iterative and is based on Fourier analysis which can be done using fast algorithms. Another advantage of this method is that it has a better performance in high-contrast media. However, it suffers from several disadvantages. It can yield artifacts due to ignoring the variation in propagation speed, the multipath effect, dispersion, and loss. Another disadvantage is related to resolution. Higher resolution requires larger bandwidth because narrow pulses are required to distinguish between the responses coming from two close targets. This disadvantage limits the use of SAR for some high-resolution imaging applications.
In radar approach the signal may be generated physically as a time domain impulse or synthetically by using a swept frequency input. Time domain image-formation algorithms (beamformers) are used to spatially focus the backscattered signals to discriminate against clutters that are caused by the heterogeneity of OI (different travel time and noise) while compensating for path-dependent attenuation and phase effects. The beamformers can be divided into two distinct categories: “data-independent” and “data-adaptive beamformers.” Data-independent beamformers typically use an assumed channel model to compensate for path-dependent propagation effects. Conversely, data-adaptive beamformers attempt to directly estimate the actual channel based on signals reflected from the OI.
The data-independent beamformers include mono-static and multi-static delay-and-sum (DAS) [21, 35–37], delay-multiply-and-sum (DMAS) [38], and improved-delay-and-sum (IDAS) [39]. Data-adaptive beamformers include robust capon beamforming (RCB) [40] and multi-static adaptive microwave imaging (MAMI) [41].
In order to know more about the radar imaging methods, we recommend the paper by Cheney and Borden [42] and the references therein. Thus, these types of MWI techniques are not considered in this book.
1.2.2 Microwave Tomography
Microwave tomography is an active wave-based noninvasive imaging method [43]. It gives us an ability to see inside and through objects with radiation other than light, without direct contact, and it will expand humankind’s sensory horizon. The physical quantities being imaged in MWT are the dielectric properties, i.e., the permittivity (ε) and the conductivity (σ) of the target.1 The value of the permittivity is related to the molecule’s dipole moment per volume while the conductivity is related to the free path length and speed of the electrons inside the material [46]. When the object is induced by external stimulation (microwave signal), the microscopic processes can deviate from their normal state and impact the overall dielectric properties. MWT techniques use microwave radiation with frequencies ranging from approximately 0.3 to 30 GHz [47], and therefore, the image pixel size may vary from meter to submillimeter.
MWT requires solving an inverse scattering problem. Except for one-dimensional (1D) problems that have analytic solutions [48], in general computational methods are utilized. In general, the relationship between the scattered field and the scattering object is a nonlinear one. This nonlinearity comes from multiple scattering effects within the object [49]. However, a linear relationship can be found sometimes for certain limited cases. Hence, the solution methods for inverse scattering problems can be categorized into linear and nonlinear ones.
In the linear approaches, approximations are made such that a linear relationship is found between the measured data and the object. Then the information on the object is obtained by solving the linear equations involved. In the X-ray tomography or the CT, the attenuation of an X-ray is linearly related to an integral summation of the attenuation experienced by the X-ray as it traverses a path [50]. In nuclear magnetic resonance imaging (NMRI), the received radio frequency signal is proportional to an integral summation of the resonating spin densities along a straight line [51]. The summation of an object function along a straight line is also known as a projection. A back-projection algorithm based on the projection-slice theorem is used to reconstruct the object function efficiently from its projections [49].
Another linear approach to solve inverse scattering problems is known as diffraction tomography, where the diffraction effect is taken into account when the scatterer is weak. A linear relationship exists between the scattered field and the object because it is only single scattering that is important. Either Born or Rytov approximations [52, 53] can be used to calculate the scattered field, which leads to a Fourier transform relationship between the scattered field and the object function. Diffraction tomography is often used in ultrasonic [54] and MWI to achieve good reconstructions when the multiple scattering effect is small. However, when multiple scattering is important as is the case for objects with strong contrasts, diffraction tomography becomes less accurate [55].
When multiple scattering effects are important, different nonlinear inverse scattering theories have been proposed to unravel the multiple scattering effects. Most nonlinear inversion algorithms require solving a number of forward scattering problems followed by an optimization procedure.
In the simulation of forward scattering, also known as forward solver, both the medium properties and the domain of inhomogeneity are assumed to be known and the Maxwell’s equations are solved to obtain the scattered fields. In the inverse scattering problem, scattered fields are measured at discrete points and the medium properties are the unknowns to be determined. Then the optimization procedure utilizes the forward solver to minimize the error between measured scattered fields and those calculated by the forward solver. The optimizer tries to do this by finding the proper composition of the closest set of dielectric properties. Figure 1.1 summarizes the block diagram of the existing methods for solving the inverse scattering problems. These methods are categorized into linear and nonlinear algorithms. The nonlinear inverse scattering algorithms are more computational intensive and complex than linear ones. However, nonlinear methods take into account more accurate physical properties of the problem and hence are more appropriate for complex media.
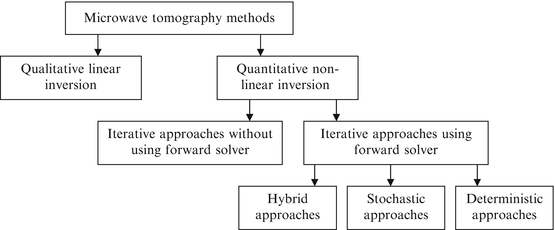

Fig. 1.1
Block diagram of the existing MWT methods
1.3 Qualitative Linear Inversion
In the category of linear approaches, the field inside the imaging medium is assumed to be equal to the incident wave. Unlike the radar-based approaches, the magnitude information is used for the reconstruction. The linear approximations, used in this category of methods, make them similar to inversion algorithms in CT. In CT, X-rays being non-diffracting (within an acceptable approximation) travel in straight lines, and therefore, the projection data measure the line integral of some object parameter along straight lines. This makes it possible to apply the Fourier slice theorem which states that the Fourier transform of a projection is equal to a slice of the two-dimensional Fourier transform of the object [56].
In approaches based on first-order approximations, the Fourier transform of the field scattered by a weak scatterer which was registered on a plane perpendicular to the normal vector of the wavefronts leads to values of the 2D Fourier transform of the object function along halfcircles. By illuminating an object from many different directions and measuring the diffracted projection data, one can in principle fill up the Fourier space with the samples of the Fourier transform of the object over an ensemble of circular arcs and then reconstruct the object by Fourier inversion. Diffraction tomography is relatively fast because it is not iterative and is based on Fourier analysis which can be done using fast algorithms.
The simplest and fastest way to linearize the inverse scattering problems is to use the first-order Born approximation [57, 58]. In the Born approximation, the total field inside the imaging domain is approximated by the incident field. In this case, the unknown is the solution of a linear first-kind Fredholm integral equation [57, 59]. This approximation is only valid for smaller objects with low contrast2 (the object represents a weak discontinuity in the propagation medium). This is a very restrictive approximation, which a vast majority of interesting inverse scattering problems do not satisfy [60]. Despite the fact that the problem is now linear, it is important to realize that it still remains ill-posed. This means that regularization is required [57].
1.4 Quantitative Nonlinear Inversion
For simple structures where inverse scattering require solving a convex optimization problem, linearization can be applied without causing a major loss of accuracy. However, as the complexity of structure increases, it is advisable to use nonlinear methods. Iterative techniques are currently one of the best options for solving the nonlinear inverse scattering problem and for performing quantitative imaging to characterizing the material composition based on conductivity and permittivity profile. In iterative techniques, the solution is found iteratively by minimizing the norm of the error between the estimated and measured scattered field values (fitness function or cost function). There are two different categories of iterative approaches that have been successfully used to solve the inverse scattering problem. The first approach uses conventional cost function which is based on the difference between the measured and predicted scattered fields for a particular choice of the material parameters. The second approach uses the same conventional cost function, formulated in terms of the “contrast sources,”added to an error functional involving the domain equation, which relates the fields inside the imaging domain to the contrast of the unknown OI. These two approaches are also distinguished by the use of a forward solver or the absence of a forward solver.
1.4.1 Forward Solver
In iterative techniques the forward solver is required to be called several times and solve the partial differential equations (PDE) in order to calculate the scattered fields associated with each transmitter for the current estimated of the OI’s electrical properties. The forward solvers are addressed using integral equation (IE) formulations of linear PDE or solving the PDE using differential equation (DE) formulations such as the finite-difference method (FDM) or the finite-element method (FEM).
Using the IE formulations, the scalar or dyadic Green’s function describing the problem’s domain has to be known beforehand. Green’s function contains information about the background medium and the problem’s boundaries. If the background medium is inhomogeneous or if the problem’s boundary is complicated (e.g., arbitrary and/or conducting), deriving and calculating Green’s function can be a complex, computationally expensive process because in nonhomogeneous background the environment can give rise to distortion, displacement, and multipath ghost images. The obvious solution for complex environments is to use a more realistic Green’s function such as Green’s function for a dielectric slab for concrete wall [33] or multipath Green’s function in a multipath environment [34]. With knowledge of Green’s function, the IE is solved using the method-of-moments (MoM), which produces a dense system of equations that can be a computational burden if solved inefficiently.
An alternative to IE formulations is solving the PDE using DE formulations such as the FDM or the FEM. Using differential operators, there is no need to know the problem’s Green function prior and the presence of an inhomogeneous background or a complicated boundary can be easily integrated without affecting the computational complexity. In addition, unlike IE formulations, using DE formulations readily produces a sparse system of equations which can be solved efficiently.
Using PDEs offers several advantages over the IE formulation: (i) the ability to model nonhomogeneous backgrounds surrounding the imaged object, (ii) ease of formulating the inverse problem theoretically for complicated boundaries, (iii) using PDEs the inverse problem becomes less computational demanding compared to IE methods, and (iv) the ability to discretize the imaging domain using arbitrary triangles (or other shapes) rather than a uniform square grid for more accurate reconstruction of the object’s properties.
1.4.2 Iterative Approaches Without Using Forward Solver
This approach does not use a forward solver and the cost function is defined based on both scattered fields outside of the OI and total fields inside the OI. This method is in the category of the “modified gradient” methods. In this approach, the optimization process is formulated in terms of an unknown contrast and an unknown total field (contrast source). At each iteration of the optimization procedure, these two unknowns have to be updated. In order to update these parameters, different techniques have been suggested. For example, in [61] the contrast and the total field are updated simultaneously as one unknown vector in the discrete domain successively using a conjugate gradient (CG) method. Another approach is that these two parameters (contrast and total field) are treated separately. This means that when optimizing over the total field, the contrast is assumed to be known (e.g., modified gradient method (MGM) [62]) and when optimizing over the contrast, the total field is assumed to be known (e.g., contrast source inversion (CSI) method [63–65]). In order to increase the robustness to noisy data and enhance the quality of reconstructions from the CSI algorithm, regularization is introduced to the cost functional at each step of the optimization process in the form of a weighted L 2-norm multiplicative constraint [65, 66]. This method is called the multiplicative regularized CSI (MRCSI) method. The two methods are applied successfully in several applications [67–69]. Although CSI and MRCSI have been successful, these methods are very efficient only if Green’s function is available and can be computed easily. The latter two conditions are applicable if the background medium is homogeneous and if the problem boundary can be easily defined within Green’s function (e.g., unbounded problem domains). In order to solve this problem and consider the inhomogeneous background medium, recently a finite-difference CSI (FDCSI) method has been introduced. The multiplicative regularization also has been applied in the FDCSI method (FD-MRCSI), and it has successfully been utilized in through-wall imaging, geophysical surveying, and biomedical applications [70, 71]. The integration of Tikhonov regularization and projection-based regularization has also been applied to CSI as hybrid regularization CSI [72, 73]. The number of unknowns in this approach is greater than that in conventional iterative approach, and therefore, it requires much more iterations to converge.
1.4.3 Iterative Approaches Using Forward Solver
In conventional approach, the differences between measured scattered fields (only outside the OI) and the scattered fields that are calculated from a possible solution are minimized. This approach is computationally complex because the system of equations has to be built at each iteration. In order to calculate the scattered field, when the electric contrast or the size of the OI is small, one may use the well-known Born approximation [74].
Another popular approximation is the Rytov approximation [74]. The Rytov approximation gave better results in imaging an object with high contrast. Basically, the result of linearizing the inverse problem is a significant loss of accuracy in predicting dielectric properties.
These methods are computationally efficient and can obtain images in a short runtime, but they usually fail when a complex media with high-contrast scatterers exist [75–77]. Forward solvers based on IE, such as the born iterative method (BIM) [78], distorted born iteration method (DBIM) [79], and local shape function (LSF) [80, 81] have also been implemented. Various attempts were made to reduce the reconstruction problem complexity by taking into account different approximations and simplifications, such as the dual-mesh scheme [82], conformal mesh reconstruction [23], adjoint technique [24], frequency-hopping reconstruction algorithms [83], and iterative multi-scaling approach [84–86]. In addition, methods for solving nonlinear PDE, such as the FDTD method, appear to be more appropriate models for the EM scattered fields.
In order to minimize the cost function and retrieve the unknown objects from the measurements, different deterministic (local optimization) and stochastic (global optimization) approaches have been proposed.
1.5 Deterministic Approaches Based on Local Optimization
These techniques proceed by minimizing the cost function using the Newton-type minimizations. They always require the selection of some kind of regularization terms. Examples of such deterministic algorithms are the modified-Newton method [20, 87], Gauss–Newton (GN) inversion [88–92], inexact-Newton (IN) [93, 94], quasi-Newton [95], Newton–Kantorovich (NK) [96], and Levenberg–Marquardt (LM) inversion [97]. The GN technique (or NK method) is also equivalent to the DBIM, as shown in [98]. The ill-posedness is usually treated by employing different regularization techniques. Various regularization techniques such as Tikhonov regularization [59, 79, 97, 99–103], Krylov subsurface regularization [20, 104], Maxwell regularizer (physical regularizer) [62], and MR [89] have been used. These traditional regularization methods, which facilitate the inversion of ill-conditioned matrices, are application-independent, which enables these methods to be used for a variety of applications. In addition, these traditional regularizations work well when only a few scatterers with small difference in dielectric properties (contrast) exist. From a computational point of view, deterministic techniques are attractive; however, they can be trapped in local minima. This means that the local-based optimization imaging techniques are only accurate if the starting trial solution is not far from the real solution or the regularization keeps the search around the global minimum. In many practical cases, it is not possible to guess the proper initial point or regularization term, and therefore, some inaccuracies in the resulting reconstructed image may appear.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree