Sequential Forward Solver

, Abas Sabouni², Travis Desell³ and Ali Ashtari⁴

(1)

Department of Electrical Engineering, University of North Dakota, Grand Forks, ND, USA

(2)

Department of Electrical Engineering, Wilkes University, Wilkes-Barre, PA, USA

(3)

Department of Computer Science, University of North Dakota, Grand Forks, ND, USA

(4)

Invenia Technical Computing, Winnipeg, MB, Canada

Abstract

In this chapter, the theory of the inverse and direct (forward) scattering problem is explained. A method for solving the inverse problem is developed in detail, and the results of some numerical simulations are used to make an in-depth analysis of the capabilities and effectiveness of the proposed approach.

2.1 Maxwell’s Equations

MWT is the process of creating the image of dielectric properties from measured electric field qualities. The dielectric properties and measured field are related by a nonlinear relationship that is modeled by Maxwell’s equations. The time-harmonic Maxwell’s equations describe the electromagnetic phenomena in macroscopic media and are given by [1]:

$\displaystyle\begin{array}{rcl} \nabla \times \boldsymbol {\mathbf{E}}(\mathbf{r}) = -j\omega \boldsymbol {\mathbf{B}}(\mathbf{r})\quad {\rm Farady^{\prime}s\,\,law},& &{}\end{array}$

(2.1)

$\displaystyle\begin{array}{rcl} \nabla \times \boldsymbol {\mathbf{H}}(\mathbf{r}) = j\omega \boldsymbol {\mathbf{D}}(\mathbf{r}) + \boldsymbol {\mathbf{J}}(\mathbf{r})\quad {\rm Ampere^{\prime}s\,\,law},& &{}\end{array}$

(2.2)

$\displaystyle\begin{array}{rcl} \nabla \cdot \boldsymbol {\mathbf{B}}(\mathbf{r}) = 0\quad {\rm Gauss^{\prime}\,\,law},& &{}\end{array}$

(2.3)

$\displaystyle\begin{array}{rcl} \nabla \cdot \boldsymbol {\mathbf{D}}(\mathbf{r}) =\rho \quad {\rm Gauss^{\prime}\,\,law},& &{}\end{array}$

(2.4)

where $\boldsymbol {\mathbf{E}}$ (V/m) is the electric field intensity, $\boldsymbol {\mathbf{H}}$ (A/m) is the magnetic field intensity, $\boldsymbol {\mathbf{B}}$ (T) is the magnetic flux density, $\boldsymbol {\mathbf{D}}$ (C∕m²) is the electric flux density, $\boldsymbol {\mathbf{J}}$ (A∕m²) is the electric current density (in phasor format), ρ (C∕m³) is electric charge density, $\mathbf{r}$ denotes the position vector, $j = \sqrt{-1}$ is the imaginary unit, and ω = 2π f (rad/Hz) is the radial frequency (f is the frequency). In order to include the information about the media in which electromagnetic phenomena occur, the constitutive relations have been used. Thus, for an isotropic and linear medium (background and OI), the relationships between the vector field and the medium become

$\displaystyle\begin{array}{rcl} \boldsymbol {\mathbf{D}}(\mathbf{r}) =\epsilon _{r}\epsilon _{0}\boldsymbol {\mathbf{E}}(\mathbf{r}),& &{}\end{array}$

(2.5)

$\displaystyle\begin{array}{rcl} \boldsymbol {\mathbf{B}}(\mathbf{r}) =\mu _{0}\mu _{r}\boldsymbol {\mathbf{H}}(\mathbf{r}),& &{}\end{array}$

(2.6)

$\displaystyle\begin{array}{rcl} \boldsymbol {\mathbf{J}}(\mathbf{r}) =\sigma \boldsymbol {\mathbf{E}}(\mathbf{r}),& &{}\end{array}$

(2.7)

where ε ₀ (F/m) is the permittivity of free space, ε _r(unit-less) is the relative permittivity (dielectric constant), μ ₀ (H/m) is the permeability of free space, μ _r(unit-less) is the relative permeability, and σ (S/m) is the electrical conductivity. We consider nonmagnetic media in this book (μ _r = 1. 0). The value of permittivity and conductivity may depend on the operating frequency. This dependency can be modeled by different formulas. In this book the Debye model has been used. Substituting Eqs. (2.5)–(2.7) into Eqs. (2.1)–(2.4), what can be seen is the dependency of the electric field on dielectric properties of the background. Solving the Maxwell’s equations in order to determine the electric field ( $\boldsymbol {\mathbf{E}}$ ) from the knowledge of the source ( $\boldsymbol {\mathbf{J}}$ ), obstacles, and medium dielectric properties (ε _r, σ) is called the forward scattering problem. The forward problem may be solved based on either IE formulation [2] or PDE formulation. In contrast, in an inverse scattering problem, the goal is to determine the physical quantities of the media (ε _r, σ) from the knowledge of the electric field ( $\boldsymbol {\mathbf{E}}$ ) at a set of receiver points and knowledge of the source ( $\boldsymbol {\mathbf{J}}$ ).

In the following sections, some challenges associated with the inverse scattering problem are explained, and some solutions are provided for them. The inverse scattering problem is always associated with ill-posedness and nonlinearity. The next section is devoted to introducing these two characteristics for the inverse problem.

2.1.1 Ill-Posedness of the Inverse Problem

In regards to ill-posedness, in the sense of Hadamard [3], any problem is considered a well-posed problem if the solution is:

In Existence: For the existence of the solution (i.e., map of dielectric properties of scatterers), as long as the best approximations are made for solving the mathematical model, we can guarantee that a solution exists.

II.

Unique: For the uniqueness of the solution, based upon the Maxwell’s equations, the scattered fields are continuous functions of incident field and dielectric properties of the background.

Therefore, the solution is unique if the knowledge of the scattering field at all positions and frequencies outside of the scatterers is available [4, 33]. Practically speaking, we can only measure the field at a finite number of locations as well as a limited number of frequencies.

As a result, the solution is always nonunique for practical problems [4, 33]. In order to overcome the nonuniqueness of the solution, a fast, accurate, and inexpensive apparatus for the generation of the interrogating field and the measurement of a large number of samples of the scattered field is necessary.

III.

Stable: The inverse scattering problem maybe unstable because a small arbitrary change in the incident field may result in an arbitrarily large change in the material parameters.

From a practical perspective, the measured scattered field is always corrupted by noise, and therefore, the solution might become unstable. Besides noise, the solution is very dependent on the observation point locations and the measurement accuracy.

After all, because of the nonuniqueness and instability of the inverse scattering problem, it is considered an ill-posed problem.

2.1.2 Nonlinearity of the Inverse Scattering Problem

In an inverse scattering problem, the aim is to determine the dielectric properties in the imaging domain from the knowledge of the scattered field.

In Eq. (2.2), the second term represents the multiplication of the field and material properties which means there is a nonlinear relation between field and material properties. When the scattered fields are only available at discrete points, this problem becomes more severe. Another reason for nonlinearity is the multiple reflections from different boundaries (Fig. 2.1).

Fig. 2.1

Multiple scattering

Significant absorption of the incident field may occur in heterogeneous object with high conductivity. For dispersive objects, different components of the signal travel at different speeds; thus the shape of the original waveform is altered. The abovementioned characteristics make the inverse problem nonlinear and complicated to solve.

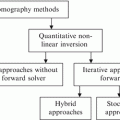
In summary, any algorithm used in order to solve the inverse scattering problems needs to consider three fundamental factors:

How to deal with the ill-posed and the ill-conditioned inverse scattering problems which is possible by using an iterative algorithm.

Developing an efficient accurate numerical method as forward solver can be computationally intensive.

Overcoming the drawbacks of two previous factors can be done using parallel computing power.

In this chapter we will address the first and second factors. We will discuss the third factor in Chap. 4.

2.1.3 Inverse Scattering Problem from Theoretical Point of View

Consider an OI inside the imaging chamber. The cross section of the OI successively is irradiated by a number of $E_{\mathrm{inc}}(\mathbf{r},\omega,\varPhi )$ . The electric field is calculated at the receivers and can be expressed in functional form as $E_{\mathrm{total}}(\mathbf{r},\omega,\epsilon (\mathbf{r},\omega ),\sigma (\mathbf{r},\omega ))$ where functions $\epsilon (\mathbf{r},\omega )$ and $\sigma (\mathbf{r},\omega )$ are the unknown distributions of permittivity and conductivity, respectively. $\mathbf{r}$ is the spatial coordinate.

The goal is to find a set of dielectric properties of the material that can generate the same scattered fields as the measured ones. The following condition needs to be satisfied:

$\displaystyle\begin{array}{rcl} \sum _{i=1}^{M}\left \vert E_{\mathrm{ total}}^{\mathrm{estimated}}({\boldsymbol r_{ i}},\omega,\epsilon (\mathbf{r},\omega ),\sigma (\mathbf{r},\omega )) - E_{\mathrm{total}}^{\mathrm{measured}}({\boldsymbol r_{ i}},\omega )\right \vert = 0,& &{}\end{array}$

(2.8)

where $E_{\mathrm{total}}^{\mathrm{measured}}({\boldsymbol r_{i}},\omega )$ is the measured total field at the M number of receiver points and the $E_{\mathrm{total}}^{\mathrm{estimated}}({\boldsymbol r_{i}},\omega,\epsilon (\mathbf{r},\omega ),\sigma (\mathbf{r},\omega ))$ is the total field computed by the forward solver. It is worth noting that inverse scattering is an overdetermined problem. There might be several arrangements of scatterers that will have very similar field values at the sampling points. There is always need for additional methods to examine if the solution physically feasible. The next section is devoted to introducing an iterative technique in order to find the permittivity and conductivity profiles that satisfies Eq. (2.8).

2.2 Iterative Technique

Iterative techniques are currently one of the best options for solving the nonlinear inverse scattering problem. These techniques have a greater probability of converging to the right solution. In this approach the scattered field outside the object is measured and the differences between this field and the scattered field of a possible solution calculated by a forward solver is minimized. Therefore, this approach needs an iterative minimization process. Figure 2.2 shows the flowchart of the iterative technique for the image reconstruction method. This method is based on optimizing a fitness function (or cost function) (2.8):

$\displaystyle\begin{array}{rcl} & & \text{min}_{\mathbf{r},\omega,\epsilon (\mathbf{r},\omega ),\sigma (\mathbf{r},\omega )}\alpha \left \|E_{\mathrm{total}}^{\mathrm{estimated}}({\boldsymbol r_{ i}}\big\vert _{i=1}^{M},\omega,\epsilon (\mathbf{r},\omega ),\sigma (\mathbf{r},\omega ))\right \| \\ & & \quad -\beta \left \|E_{\mathrm{total}}^{\mathrm{measured}}({\boldsymbol r_{ i}}\big\vert _{i=1}^{M},\omega )\right \| + R(\omega,\epsilon (\mathbf{r},\omega ),\sigma (\mathbf{r},\omega )).{}\end{array}$

(2.9)

The constants α and β can be heuristically determined for a certain class of scatterers. This kind of calibration is based on the assumption that a certain class of scatterers can be inspected and the optimal values found for α and β can be used for a class of similar scatterers. In the third term of Eq. (2.9), the function $R(\omega,\epsilon (\mathbf{r},\omega ),\sigma (\mathbf{r},\omega ))$ is a term that can include a priori information (constraints of dielectric properties) or their gradient configuration to be inspected and can play the role of regularization. The general approach for regularizing an ill-posed problem is to set “appropriate” constraints on the solution, e.g., limiting the norm of the solution or enforcing the solution to lie in an appropriate subspace [5]. This term is needed because of the ill-posedness of the inverse problem, and in this book, a priori information is used as regularization term.

Fig. 2.2

Flowchart of the iterative technique

2.3 Time Domain Algorithm

The majority of the proposed inverse scattering algorithms have used monochromatic (single-frequency) excitation [6–16]. Although using monochromatic incidences has been applied successfully to different applications of MWI, it has a significant shortcoming. It has been proven that due to the ill-posedness and nonlinearity of the problem the inverse algorithms fail if they only use monochromatic incidences [17]. The frequency-hopping algorithm has been proposed to overcome this problem [18–23]. In this method, for the data acquisition, a continuous incident wave spectrum is necessary to illuminate the object at different frequencies and also UWB probe is required to collect the electric field. Consequently, for analyzing such a measurement setup with multiple frequencies, it is better to use a time domain solver. This is the reason that we select the time domain numerical method as the forward solver.

2.3.1 Time Domain Forward Scattering Problem

The goal is to calculate the scattered fields when the object, background medium, and source are completely known. This is called the forward scattering problem. In order to solve this problem, the same as the inverse problem, Maxwell’s equations need to be used. For calculating the scattered field in some problems the analytical solutions, in the form of eigenfunction expansions, are available. However, when the geometry of the scatterer is complex, these analytical methods are not applicable. In such cases, we have to use approximations and/or numerical methods. Throughout this book, the FDTD numerical method has been proposed as a forward solver.

FDTD is a numerical method used to solve Maxwell’s equations in the time domain by applying central difference to time and space derivation in a wide range of applications [24].

One benefit of the time domain approach is that it yields a broadband output from a single execution of the program. However, the main reason for using the FDTD approach is its effectiveness as a technique for calculating electromagnetic fields in multilayer inhomogeneous objects. With a large number of unknown parameters related to the object under the test, the FDTD approach outpaces other methods in efficiency and provides accurate results of the field penetration into objects. In FDTD methods, Maxwell’s equations are solved in a closed area. This means that the solution area for scattering problems in an infinite space, such as the one that we are dealing with, needs to be truncated by an absorbing boundary condition (ABC) [24]. We chose to use the uniaxial perfectly match layer (UPML) which is a very efficient ABC [25]. The UPML ABC is based on an artificial absorbing layer surrounding the simulation region (see [24] for more details).

2.4 Debye Model

The frequency dependence of materials can be efficiently described in the time domain using Debye or Lorentz models [24]. These models can be expressed in different orders. The higher-order models can accurately represent arbitrary dispersive medium at the expense of computational cost and complexity [26]. The Debye equation is given by

$\displaystyle\begin{array}{rcl} \epsilon _{r}(\omega ) =\epsilon _{\infty } +\sum _{ p=0}^{p_{\mathrm{max}} } \frac{(\epsilon _{s} -\epsilon _{\infty })} {1 + (j\omega \tau _{p})^{1-\alpha _{p}}} - j\frac{\sigma _{s}} {\omega \epsilon _{0}},& &{}\end{array}$

(2.10)

where α _pis a dimensionless weight, τ _pis the relaxation time of the pth Debye function, ε ₀ is the permittivity of the free space, ε _sand ε _∞are the dielectric constants at zero (static) and infinite frequencies, respectively. σ _sis the conductivity at low frequency, and ω is the angular frequency. In order to maintain the simplicity of the method and to reduce computational cost, the first-order Debye model is employed [27, 28]. If p = 0 and α ₀ = 0, therefore,

$\displaystyle\begin{array}{rcl} \epsilon _{r} - j \frac{\sigma } {\omega \epsilon _{0}} =\epsilon _{\infty } + \frac{\epsilon _{s} -\epsilon _{\infty }} {1 + j\omega \tau _{0}} - j\frac{\sigma _{s}} {\omega \epsilon _{0}},& &{}\end{array}$