Kinetics of Radioactive Decay

(3.1)

where N is the number of radioactive atoms present, and λ is referred to as the decay constant of the radionuclide . As can be seen from Eq. (3.1), it is a small fraction of the radioactive atoms that decays in a very short period of time. The unit of λ is (time)⁻¹. Thus, if λ is 0.2 s⁻¹ for a radionuclide, then 20 % of the radioactive atoms present will disappear per second.

The disintegration rate −dN/dt is referred to as the radioactivity or simply the activity of the radionuclide and denoted by A. It should be understood from Eq. (3.1) that the same amount of radioactivity means the same disintegration rate for any radionuclide, but the total number of atoms present and the decay constants differ for different radionuclides. For example, a radioactive sample A containing 10⁶ atoms and with λ = 0.01 min⁻¹ would give the same disintegration rate (10,000 disintegrations per minute) as that by a radioactive sample B containing 2 × 10⁶ atoms and with a decay constant 0.005 min⁻¹.

Now from the preceding discussion, the following equation can be written:

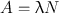
$A=\uplambda N$

(3.2)

From a knowledge of the decay constant and radioactivity of a radionuclide, one can calculate the total number of atoms or mass of the radionuclides present (using Avogadro’s number 1 g atom = 6.02 × 10²³ atoms).

Because Eq. (3.1) is a first-order differential equation, the solution of this equation by integration leads to

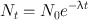
${{N}_{t}}={{N}_{0}}{{e}^{-\uplambda t}}$

(3.3)

where N ₀ and N _tare the number of radioactive atoms at t = 0 and time t, respectively. Equation (3.3) is an exponential equation indicating that the radioactivity decays exponentially. By multiplying both sides of Eq. (3.3) by λ, one obtains

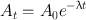
${{A}_{t}}={{A}_{0}}{{e}^{-\uplambda t}}$

(3.4)

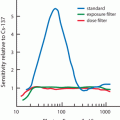
The factor e ^−λ ^tis called the decay factor. The decay factor becomes e ^+λ ^tif the activity at time t before t = 0 is to be determined. The plot of activity versus time on a linear graph gives an exponential curve, as shown in Fig. 3.1. However, if the activity is plotted against time on semilogarithmic paper, a straight line results, as shown in Fig. 3.2.

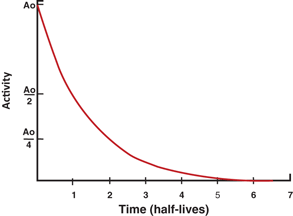
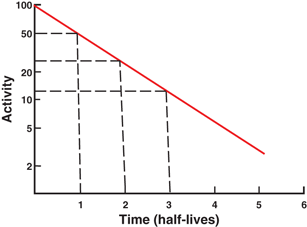
Fig. 3.1

Plot of radioactivity versustime on a linear graph indicating an exponential curve.

Fig. 3.2

Plot of radioactivity against time on a semilogarithmic graph indicating a straight line. The half-life of the radionuclide can be determined from the slope of the line, which is given as the decay constant λ. Alternatively, an activity and half its value and their corresponding times are read from the plot. The difference in the two time readings gives the half-life.

Half-Life

Every radionuclide is characterized by a half-life , which is defined as the time required to reduce its initial activity to one half. It is usually denoted by t _1/2 and is unique for a radionuclide. It is related to the decay constant λ of a radionuclide by

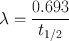
$\lambda =\frac{0.693}{{{t}_{1/2}}}$

(3.5)

From the definition of half-life, it is understood that A ₀ is reduced to A ₀/2 in one half-life; to A ₀/4, that is, to A ₀/2² in two half-lives; to A ₀/8, that is, to A ₀/2³ in three half-lives; and so forth. In n half-lives of decay, it is reduced to A ₀/2ⁿ. Thus, the radioactivity A _tat time t can be calculated from the initial radioactivity A ₀ by

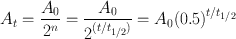
${{A}_{t}}=\frac{{{A}_{0}}}{{{2}^{n}}}=\frac{{{A}_{0}}}{{{2}^{(t/{{t}_{1/2}})}}}={{A}_{0}}{{(0.5)}^{t/{{t}_{1/2}}}}$

(3.6)

where t is the time of decay. Here, t/t _1/2 can be an integer or a fraction depending on t and t _1/2. For example, a radioactive sample with t _1/2 = 3.2 days decaying at a rate of 10,000 disintegrations per minute would give, after seven days of decay, 10,000/2^(7/3.2) = 10,000/2^2.2 = 10,000/4.59 = 2178 disintegrations per minute.

It should be noted that ten half-lives of decay reduce the radioactivity by a factor of about 1000(2¹⁰ = 1024), or to 0.1 % of the initial activity.

The half-life of a radionuclide is determined by measuring the radioactivity at different time intervals and plotting them on semilogarithmic paper, as shown in Fig. 3.2 . An initial activity and half its value are read from the line, and the corresponding times are noted. The difference in time between the two readings gives the half-life of the radionuclide. For a very long-lived radionuclide, the half-life is determined by Eq. (3.2) from a knowledge of its activity and the number of atoms present. The number of atoms N can be calculated from the weight W of the radionuclide with atomic weight A and Avogadro’s number 6.02 × 10²³ atoms per g .atom as follows:

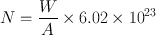
$N=\frac{W}{A}\times 6.02\times {{10}^{23}}$

(3.7)

When two or more radionuclides are present in a sample, the measured count of such a sample comprises counts of all individual radionuclides . A semilogarithmic plot of the activity of a two-component sample versus time is shown in Fig. 3.3. The half-life of each of the two radionuclides can be determined by what is called the peeling or stripping method. In this method, first, the tail part (second component) of the curve is extrapolated as a straight line up to the ordinate, and its half-life can be determined as mentioned previously (e.g. 27 h). Second, the activity values on this line are subtracted from those on the composite line to obtain the activity values for the first component. A straight line is drawn through these points, and the half-life of the first component is determined (e.g. 5.8 h). The stripping method can be applied to more than two components in the similar manner.

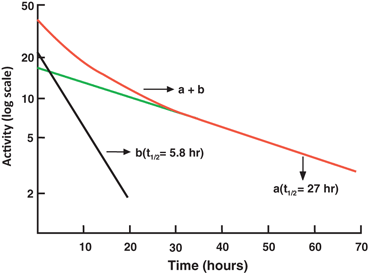
Fig. 3.3

A composite radioactive decay curve for a sample containing two radionuclides of different half-lives. The long-lived component (a) has a half-life of 27 h and the short-lived component (b) has a half-life of 5.8 h

Mean Life

Another relevant quantity of a radionuclide is its mean life , which is the average lifetime of a group of radionuclides. It is denoted by τ and is related to the decay constant λ and half-life t _1/2 as follows:

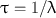
$\uptau ={1}/{\uplambda}$

(3.8)

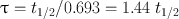
$\uptau ={{t}_{1/2}}/{0.693}=1.44\;{{t}_{1/2}}$

(3.9)

In one mean life, the activity of a radionuclide is reduced to 37 % of its initial value.

Effective Half-Life

As already mentioned, a radionuclide decays exponentially with a definite half-life, which is called the physical half-life , denoted by T _p(or t _1/2). The physical half-life of a radionuclide is independent of its physicochemical conditions. Analogous to physical decay, radiopharmaceuticals administered to humans disappear exponentially from the biological system through fecal excretion, urinary excretion, perspiration, or other routes. Thus, after in vivo administration every radiopharmaceutical has a biological half-life (T _b) , which is defined as the time needed for half of the radiopharmaceutical to disappear from the biologic system. It is related to decay constant λ_bby λ_b = 0.693/T _b.

Obviously, in any biologic system, the loss of a radiopharmaceutical is due to both the physical decay of the radionuclide and the biologic elimination of the radiopharmaceutical. The net or effective rate (λ_e) of loss of radioactivity is then related to λ_pand λ_bby

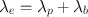
${{\lambda}_{e}}={{\lambda}_{p}}+{{\lambda}_{b}}$

(3.10)

Because λ = 0.693/t _1/2, it follows that

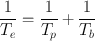
$\frac{1}{{{T}_{e}}}=\frac{1}{{{T}_{p}}}+\frac{1}{{{T}_{b}}}$

(3.11)

or,

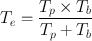
${{T}_{e}}=\frac{{{T}_{p}}\times {{T}_{b}}}{{{T}_{p}}+{{T}_{b}}}$

(3.12)

The effective half-life , T _e, is always less than the shorter of T _por T _b. For a very long T _pand a short T _b, T _eis almost equal to T _b. Similarly, for a very long T _band short T _p, T _eis almost equal to T _p.

Only gold members can continue reading. Log In or Register to continue