We introduce the fundamental aspects of MT, of MT MR imaging, and the respective analysis techniques. We then review the applications of MT MR imaging to multiple sclerosis. Finally we review the technique’s contribution to our understanding of this disease.
Signal intensities derived by conventional MR imaging are mainly based on the different relaxation characteristics of H protons in water molecules. The tissue-specific microstructure surrounding these water molecules determines the respective relaxation behavior and hence their intrinsic T 1 and T 2 relaxation times. This is the basis for the excellent tissue contrast that has made MR imaging an invaluable tool for the diagnosis and management of disorders of the central nervous system (CNS) and especially of white matter (WM) diseases.
Magnetization transfer (MT) MR imaging is an approach to explore nonwater components in tissue. Protons bound to larger molecules have relaxation properties that make them invisible for a conventional MR measurement. However, the pool of bound protons can be indirectly quantified by MR imaging sequences that use the mechanism of energy exchange between bound protons and water protons, commonly termed MT, and observe the modulation of energy of tissue water protons that results from this process. As the extent of MT largely depends on the structure and biochemical environment of the macromolecules, MT MR imaging thus provides a new and different window into tissue composition and microstructure. The attraction of using MT for assessing tissue changes in multiple sclerosis (MS) is obvious. While conventional MR imaging lacks specificity, MT MR imaging is expected to add independent and quantitative microstructural information on MS-related tissue changes. This is the reason why MT MR imaging has been widely applied in MS research over the past years.
MR sequences for generating MT contrast (MTC) are readily available on modern scanners. MT MR imaging is a robust technique with high reproducibility. The absolute MTC, however, largely depends on sequence and scanner characteristics. Thus, the choice of MT sequence parameters has a huge impact on the magnitude of MTC observed and the resulting sensitivity for the detection of tissue changes. This dependence may be well used for maximizing the MTC but also goes along with the inherent problem of potentially significant variations in the MTC generated with different scanners and at different sites. As a consequence, reported absolute values per se may be insufficient or even misleading when attempting to interpret the results of MT studies and the performance of multicenter studies can be challenging. After introducing fundamental aspects of MT, of MT MR imaging, and the respective analysis techniques we review the applications of this technique to MS and its contribution to our understanding of the disease.
The phenomenon of magnetization transfer
The two-pool model traditionally serves as a simplified model for understanding the phenomenon of MT. Brain tissue is commonly considered as a system with two different kinds of 1 H protons. One pool represents the protons of the free mobile tissue water, whereas the other represents motional restricted H protons that are bound to macromolecules. In the case of brain tissue the bound protons are mainly associated with the myelin lipids and proteins ( Fig. 1 ). Compartmentalization of 1 H spins in terms of their mobility can also be demonstrated in the frequency domain, where bulk water exhibits a very narrow line width while the signal of the motional restricted 1 H protons is significantly broadened. This is also the reason why protons bound to macromolecules are not observable with conventional MR imaging. Recent studies have extended the two-pool model by separating the liquid pool into more dedicated water pools. Although the two-pool model is sufficient to describe longitudinal relaxation in brain tissue, the extended model may be particularly important for a T 2 relaxation analysis.
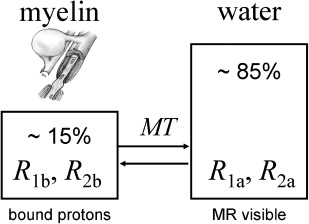
The most important feature of the two-pool model is the exchange of magnetization between both pools. The amount of MT is usually expressed by a fundamental rate constant or, depending on notation, by a first-order forward and backward transfer rate.
Two different models are currently used to explain the mechanisms of MT between water and protons of macromolecules. Both are based on the nuclear Overhauser effect (NOE), which provides dipole-dipole coupling over very short distances only. One model is based on the assumption that the nonexchangeable protons of macromolecules exchange magnetization with the water protons of the hydration layer by NOE cross relaxation, where hydration water exchanges rapidly with free mobile tissue water. In the other model, exchange of magnetization by NOE cross-relaxation occurs between nonexchangeable protons and exchangeable protons of the NH and OH groups of the macromolecules, which in turn exchange sufficiently fast with tissue water protons (proton exchange). In the latter model no hydration layer is involved in MT.
So far the dominant mechanism in brain tissue that accounts for an efficient MT between water and macromolecules is still unclear. Results from high-resolution MR spectroscopy suggest that the water of the hydration layer has a residence time in the range of subnanoseconds. This short residence time is also confirmed by relaxation time measurements of deuteron and 17 O spins. As a consequence, the hydration water does not appear to stay sufficiently long in contact with the macromolecular surface for a significant contribution to the MT via the NOE. On the other hand, there is evidence that some globular proteins contain internal hydration water molecules that exchange considerably more slowly with the bulk water. MT thus is probably restricted to a few sites of the macromolecules, ie, those with relatively long-lived hydration water. Experiments with lipid suspensions and isotopically substituted protons support this view and have shown that the exchange of magnetization is not chemical. Observations of a strong pH effect on MT also suggest the exchange of protons as an important mechanism for MT.
In summary, although several potential transfer processes of magnetization have been identified, it is still unclear which one plays the dominant role in the CNS. For the interpretation of MT experiments, knowledge of the exact mechanism involved would certainly be an advantage. In the absence of such an understanding, we currently use to consider MT as a phenomenon that is linked primarily to the density of macromolecules. Furthermore, it is specific for the CNS that the macromolecular density is largely driven by the macromolecules contained in myelin. As a consequence, measurements of MT are especially sensitive to changes in myelination but it is increasingly recognized that the information provided goes far beyond WM.
Imaging of the magnetization transfer
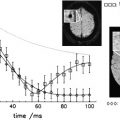
MT MR imaging intends to depict differences in the effect of MT within a given tissue or organ by generating MTC. This is achieved by employing trains of spectral selective radiofrequency (RF) pulses to selectively saturate the longitudinal magnetization of the bound protons, ie, to reduce their magnetization toward zero. This magnetization (or energy) is then “exchanged” with the MR visible water pool (“saturation transfer”), ie, the free water protons also become partly saturated. Consequently, the MR signal intensity that is proportional to the longitudinal magnetization of the water pool goes down ( Fig. 2 ). In the two-pool model the amount of signal decrease depends on the rate of exchange, the fractional size of the bound pool, and the intrinsic T 1 and T 2 relaxation times of each pool. Basically, all six pool parameters can be estimated from a series of saturation transfer experiments with varying frequency or power of the saturation pulses. However, because of the extensive measurement time that would be necessary and because of complex postprocessing, such an approach is still not feasible in clinical routine. Instead, “conventional” MT measurements assess the relative magnitude of MT, ie, the magnetization transfer ratio (MTR), which can be derived from the combination of a single saturation transfer measurement and a reference measurement. For these measurements, it is desirable to normalize the signal drop caused by MT, therefore it has become common practice to calculate the MTR according to:
where S s is the signal intensity obtained under selective saturation and S 0 is a reference measurement without any saturation pulse. The MTR can be calculated for an individual region but also for a whole image by doing this calculation pixelwise ( Fig. 3 ).
The MTR has become a very attractive measure because it is sensitive to MT, and it is fast and easy to measure. Moreover, it is a quantitative measure in the sense that it is reproducible and comparable among subjects provided the same sequence is used. However, it is often overlooked that the MTR is generally a weighted function of all pool parameters and therefore strongly depends on the sequence parameters and on the properties of the saturation pulses. This is also the reason why the variation of published MTR values is extremely high.
MTR mapping can be done with almost every pulse sequence just by adding spectral selective saturation pulses. The saturation is usually done with an off-resonance saturation pulse but can also be performed on-resonance. On-resonant pulses consist of a binomial series of rectangular RF pulses. Their saturation effect is comparable with the effect of off-resonance pulses and they are much shorter and therefore more efficient; however, they are also more sensitive to B 0 variations and imperfections of pulse timing. MTR mapping is usually done with proton density weighted gradient echo sequences, but also other sequences such as a spin echo sequence or even a true fast imaging with steady state precession (FISP) sequence can be used. An interesting option is the use of a gradient echo sequence with a short repetition time. This approach allows true three-dimensional imaging and provides a high signal-to-noise ratio in addition to a strong MT saturation effect. The latter is caused by the fact that a shorter repetition time allows more saturation pulses in a given time and therefore a higher rate of RF saturation. It should be noted, however, that in such a setting the signal reduction due to the MT effect can be partly counteracted by T 1 relaxation, ie, MT also reduces T 1 , which leads to an increase in signal intensity in T 1 -weighted sequences.
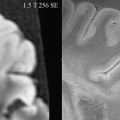
Because of the saturation pulses, MT sequences produce a higher power deposition in brain tissue than conventional sequences. While the restriction by the specific absorption rate (SAR) at 1.5 T is usually small for MT sequences, SAR limits hamper the implementation of MT sequences at higher field strength. Therefore, parallel imaging techniques or SAR reduction techniques are required to take advantage of the full benefits provided by high field strengths ( Fig. 4 ).
Imaging of the magnetization transfer
MT MR imaging intends to depict differences in the effect of MT within a given tissue or organ by generating MTC. This is achieved by employing trains of spectral selective radiofrequency (RF) pulses to selectively saturate the longitudinal magnetization of the bound protons, ie, to reduce their magnetization toward zero. This magnetization (or energy) is then “exchanged” with the MR visible water pool (“saturation transfer”), ie, the free water protons also become partly saturated. Consequently, the MR signal intensity that is proportional to the longitudinal magnetization of the water pool goes down ( Fig. 2 ). In the two-pool model the amount of signal decrease depends on the rate of exchange, the fractional size of the bound pool, and the intrinsic T 1 and T 2 relaxation times of each pool. Basically, all six pool parameters can be estimated from a series of saturation transfer experiments with varying frequency or power of the saturation pulses. However, because of the extensive measurement time that would be necessary and because of complex postprocessing, such an approach is still not feasible in clinical routine. Instead, “conventional” MT measurements assess the relative magnitude of MT, ie, the magnetization transfer ratio (MTR), which can be derived from the combination of a single saturation transfer measurement and a reference measurement. For these measurements, it is desirable to normalize the signal drop caused by MT, therefore it has become common practice to calculate the MTR according to:
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree