with labels 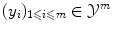 . If the number of possible labels is finite and small, then we can be interested in classification, i.e. in finding the label to assign to a new object based on the given examples. Otherwise, if the labels are values in a vector space, we can be interested in regression, i.e. in extrapolating previously observed values to any new object. Thus classification and regression tasks can be embedded in a similar framework, one aiming to predict discrete labels and the other one to continuous values.
. If the number of possible labels is finite and small, then we can be interested in classification, i.e. in finding the label to assign to a new object based on the given examples. Otherwise, if the labels are values in a vector space, we can be interested in regression, i.e. in extrapolating previously observed values to any new object. Thus classification and regression tasks can be embedded in a similar framework, one aiming to predict discrete labels and the other one to continuous values.
The objects 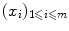 are often named patterns, or cases, inputs, instances, or observations. The
are often named patterns, or cases, inputs, instances, or observations. The 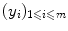 are called labels, or targets, outputs or sometimes also observations. The set of all correspondences
are called labels, or targets, outputs or sometimes also observations. The set of all correspondences 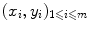 given as examples is called the training set, whereas we name test set the set of new objects for which we would like to guess the label by extracting knowledge from the examples in the training set.
given as examples is called the training set, whereas we name test set the set of new objects for which we would like to guess the label by extracting knowledge from the examples in the training set.
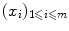 are often named patterns, or cases, inputs, instances, or observations. The
are often named patterns, or cases, inputs, instances, or observations. The 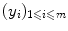 are called labels, or targets, outputs or sometimes also observations. The set of all correspondences
are called labels, or targets, outputs or sometimes also observations. The set of all correspondences 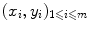 given as examples is called the training set, whereas we name test set the set of new objects for which we would like to guess the label by extracting knowledge from the examples in the training set.
given as examples is called the training set, whereas we name test set the set of new objects for which we would like to guess the label by extracting knowledge from the examples in the training set.In both cases, classification or regression, we aim to generalize the correspondences (x i , y i ) to a function f defined on the set 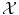 of all possible objects and with values in the set
of all possible objects and with values in the set 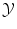 of all possible labels. The label predicted for a new test object x would then be f(x). Here we have no particular assumption on the spaces
of all possible labels. The label predicted for a new test object x would then be f(x). Here we have no particular assumption on the spaces 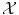 and
and 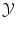 except that
except that 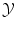 should be a vector space if we are interested in regression (in order to extrapolate continuously between any two values). But we have a strong intuitive assumption on f: it should generalize as well as possible the given examples, i.e. if x is close to an already observed input x i , its output f(x) should be close to the already observed output y i . The whole difficulty consists in defining precisely what we mean by “close” in the spaces
should be a vector space if we are interested in regression (in order to extrapolate continuously between any two values). But we have a strong intuitive assumption on f: it should generalize as well as possible the given examples, i.e. if x is close to an already observed input x i , its output f(x) should be close to the already observed output y i . The whole difficulty consists in defining precisely what we mean by “close” in the spaces 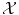 and
and 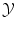 . More precisely, we need to quantify the similarity of inputs in
. More precisely, we need to quantify the similarity of inputs in 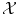 and the cost of assigning wrong outputs in
and the cost of assigning wrong outputs in 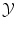 .
.
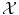 of all possible objects and with values in the set
of all possible objects and with values in the set 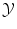 of all possible labels. The label predicted for a new test object x would then be f(x). Here we have no particular assumption on the spaces
of all possible labels. The label predicted for a new test object x would then be f(x). Here we have no particular assumption on the spaces 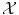 and
and 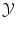 except that
except that 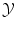 should be a vector space if we are interested in regression (in order to extrapolate continuously between any two values). But we have a strong intuitive assumption on f: it should generalize as well as possible the given examples, i.e. if x is close to an already observed input x i , its output f(x) should be close to the already observed output y i . The whole difficulty consists in defining precisely what we mean by “close” in the spaces
should be a vector space if we are interested in regression (in order to extrapolate continuously between any two values). But we have a strong intuitive assumption on f: it should generalize as well as possible the given examples, i.e. if x is close to an already observed input x i , its output f(x) should be close to the already observed output y i . The whole difficulty consists in defining precisely what we mean by “close” in the spaces 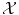 and
and 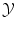 . More precisely, we need to quantify the similarity of inputs in
. More precisely, we need to quantify the similarity of inputs in 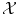 and the cost of assigning wrong outputs in
and the cost of assigning wrong outputs in 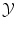 .
.Loss function
Generally, expressing a distance or similarity measure in 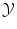 is easy. In the case of regression, the Euclidean distance in
is easy. In the case of regression, the Euclidean distance in 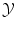 is often a simple, convenient choice. However we can consider other functions than distances, provided they express the cost of assigning a wrong label. We call the loss function the sum of the costs (or losses) of all mistakes made when we consider a particular possible solution f and apply it to all known examples. For instance we can choose:
is often a simple, convenient choice. However we can consider other functions than distances, provided they express the cost of assigning a wrong label. We call the loss function the sum of the costs (or losses) of all mistakes made when we consider a particular possible solution f and apply it to all known examples. For instance we can choose:
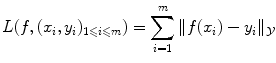
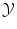 is easy. In the case of regression, the Euclidean distance in
is easy. In the case of regression, the Euclidean distance in 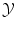 is often a simple, convenient choice. However we can consider other functions than distances, provided they express the cost of assigning a wrong label. We call the loss function the sum of the costs (or losses) of all mistakes made when we consider a particular possible solution f and apply it to all known examples. For instance we can choose:
is often a simple, convenient choice. However we can consider other functions than distances, provided they express the cost of assigning a wrong label. We call the loss function the sum of the costs (or losses) of all mistakes made when we consider a particular possible solution f and apply it to all known examples. For instance we can choose: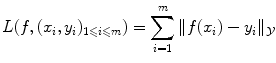
Duality between features and similarity measures
On the other hand, expressing a similarity measure in 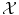 is much more difficult and lies at the core of machine learning. Either the space
is much more difficult and lies at the core of machine learning. Either the space 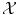 has been carefully chosen so that the representation of the observed objects x i are meaningful, in the sense that their “natural” distance in
has been carefully chosen so that the representation of the observed objects x i are meaningful, in the sense that their “natural” distance in 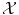 (say the Euclidean distance if
(say the Euclidean distance if 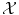 is a vector space) is meaningful, in which case learning will be easy; either
is a vector space) is meaningful, in which case learning will be easy; either 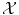 is non-trivial and we need to choose a set of N sensible features (seen as a function Φ from
is non-trivial and we need to choose a set of N sensible features (seen as a function Φ from 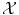 to
to 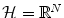 ), so that if we compute these features Φ(x i ) for each x i , we can consider a more natural distance in the feature space
), so that if we compute these features Φ(x i ) for each x i , we can consider a more natural distance in the feature space 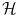 . From a certain point of view, choosing a sensible feature map Φ or choosing a sensible distance in
. From a certain point of view, choosing a sensible feature map Φ or choosing a sensible distance in 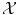 (or in the feature space
(or in the feature space 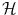 ) are equivalent problems, and hence equivalently hard in the general case.
) are equivalent problems, and hence equivalently hard in the general case.
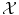 is much more difficult and lies at the core of machine learning. Either the space
is much more difficult and lies at the core of machine learning. Either the space 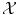 has been carefully chosen so that the representation of the observed objects x i are meaningful, in the sense that their “natural” distance in
has been carefully chosen so that the representation of the observed objects x i are meaningful, in the sense that their “natural” distance in 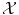 (say the Euclidean distance if
(say the Euclidean distance if 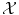 is a vector space) is meaningful, in which case learning will be easy; either
is a vector space) is meaningful, in which case learning will be easy; either 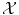 is non-trivial and we need to choose a set of N sensible features (seen as a function Φ from
is non-trivial and we need to choose a set of N sensible features (seen as a function Φ from 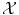 to
to 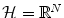 ), so that if we compute these features Φ(x i ) for each x i , we can consider a more natural distance in the feature space
), so that if we compute these features Φ(x i ) for each x i , we can consider a more natural distance in the feature space 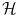 . From a certain point of view, choosing a sensible feature map Φ or choosing a sensible distance in
. From a certain point of view, choosing a sensible feature map Φ or choosing a sensible distance in 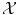 (or in the feature space
(or in the feature space 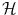 ) are equivalent problems, and hence equivalently hard in the general case.
) are equivalent problems, and hence equivalently hard in the general case.Optimization problem over functions
The problem of classification or regression can be written as an optimization problem over all possible functions f: find the best function f from 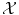 to
to 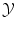 such that it minimizes
such that it minimizes
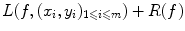 where R(f) is a regularizer constraining f to be smooth in some way with respect to the similarity measure chosen in
where R(f) is a regularizer constraining f to be smooth in some way with respect to the similarity measure chosen in 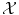 . Note that we could also have restricted f to be a member of a small function space
. Note that we could also have restricted f to be a member of a small function space 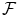 . There are very nice theoretical results concerning the function space in the kernel case (see for example Sect. 2.3 about ridge regression).
. There are very nice theoretical results concerning the function space in the kernel case (see for example Sect. 2.3 about ridge regression).
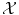 to
to 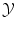 such that it minimizes
such that it minimizes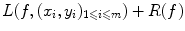
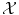 . Note that we could also have restricted f to be a member of a small function space
. Note that we could also have restricted f to be a member of a small function space 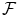 . There are very nice theoretical results concerning the function space in the kernel case (see for example Sect. 2.3 about ridge regression).
. There are very nice theoretical results concerning the function space in the kernel case (see for example Sect. 2.3 about ridge regression).2.2 Kernels
This section aims to define kernels and to explain all facets of the concept. It is a preliminary step to the following sections dedicated to kernel algorithms themselves.
A kernel is any symmetric similarity measure on 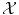
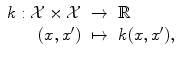 that is, a symmetric function that, given two inputs x and x′, returns a real number characterizing their similarity (cf. [1, 3, 4, 7, 10]).
that is, a symmetric function that, given two inputs x and x′, returns a real number characterizing their similarity (cf. [1, 3, 4, 7, 10]).
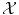
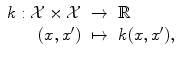
Kernels as inner products in the feature space
In the general case, either 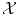 is not a vector space, or the natural Euclidean inner product in
is not a vector space, or the natural Euclidean inner product in 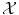 is not particularly relevant as a similarity measure. Most often, a set of possibly-meaningful features is available, and we can consequently use the feature map
is not particularly relevant as a similarity measure. Most often, a set of possibly-meaningful features is available, and we can consequently use the feature map
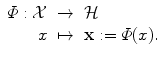
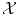 is not a vector space, or the natural Euclidean inner product in
is not a vector space, or the natural Euclidean inner product in 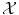 is not particularly relevant as a similarity measure. Most often, a set of possibly-meaningful features is available, and we can consequently use the feature map
is not particularly relevant as a similarity measure. Most often, a set of possibly-meaningful features is available, and we can consequently use the feature map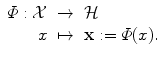
Φ will typically be a nonlinear map with values in a vector space. It could for example compute products of components of the input x. We have used a bold face 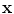 to denote the vectorial representation of x in the feature space
to denote the vectorial representation of x in the feature space 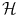 . We will follow this convention throughout the chapter.
. We will follow this convention throughout the chapter.
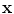 to denote the vectorial representation of x in the feature space
to denote the vectorial representation of x in the feature space  . We will follow this convention throughout the chapter.
. We will follow this convention throughout the chapter.We can use the non-linear embedding of the data into the linear space  via Φ to define a similarity measure from the dot product in
via Φ to define a similarity measure from the dot product in  ,
,
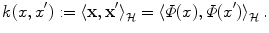
The freedom to choose the mapping Φ will enable us to design a large variety of similarity measures and learning algorithms. The transformation of x i into 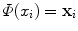 can be seen as a change of the inputs, i.e. as a new model of the initial problem. However, we will see later that, in some cases, we won’t need to do this transformation explicitly, which is very convenient if the number of features considered (or the dimension of
can be seen as a change of the inputs, i.e. as a new model of the initial problem. However, we will see later that, in some cases, we won’t need to do this transformation explicitly, which is very convenient if the number of features considered (or the dimension of 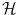 ) is high.
) is high.
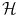 via Φ to define a similarity measure from the dot product in
via Φ to define a similarity measure from the dot product in 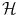 ,
,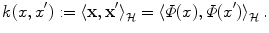
(1)
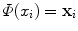 can be seen as a change of the inputs, i.e. as a new model of the initial problem. However, we will see later that, in some cases, we won’t need to do this transformation explicitly, which is very convenient if the number of features considered (or the dimension of
can be seen as a change of the inputs, i.e. as a new model of the initial problem. However, we will see later that, in some cases, we won’t need to do this transformation explicitly, which is very convenient if the number of features considered (or the dimension of 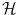 ) is high.
) is high.Geometrical interpretation and kernel trick
Through the definition of k, we can provide geometric interpretation of the input data:
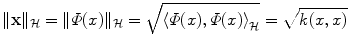 is the length (or norm) of x in the feature space. Similarly, k(x, x′) computes the cosine of the angle between the vectors
is the length (or norm) of x in the feature space. Similarly, k(x, x′) computes the cosine of the angle between the vectors 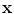 and
and 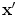 , provided they are normalized to length 1. Likewise, the distance between two vectors is computed as the length of the difference vector:
, provided they are normalized to length 1. Likewise, the distance between two vectors is computed as the length of the difference vector:
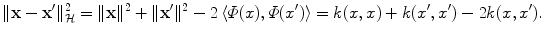
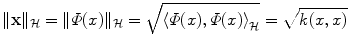
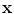 and
and 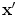 , provided they are normalized to length 1. Likewise, the distance between two vectors is computed as the length of the difference vector:
, provided they are normalized to length 1. Likewise, the distance between two vectors is computed as the length of the difference vector: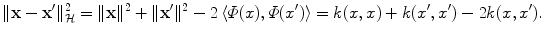
The interesting point is that we could consider any such similarity measure k and forget about the associated Φ: we would still be able to compute lengths, distances and angles with the only knowledge of k thanks to these formulas. This framework allows us to deal with the patterns geometrically through a understated non-linear embedding, and thus lets us study learning algorithms using linear algebra and analytic geometry. This is known as the kernel trick: any algorithm dedicated to Euclidean geometry involving only distances, lengths and angles can be kernelized by replacing all occurrences of these geometric quantities by their expressions as a function of k. Next section is dedicated to such kernelizations.
Examples of kernels
Let us introduce the most-commonly used kernels. They are namely: the polynomial kernel
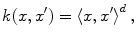 and the Gaussian
and the Gaussian
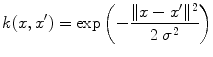 for suitable choices of d and σ. Let us focus on the Gaussian case: the similarity measure k(x, x′) between x and x′ is always positive, and is maximal when x = x′. All points
for suitable choices of d and σ. Let us focus on the Gaussian case: the similarity measure k(x, x′) between x and x′ is always positive, and is maximal when x = x′. All points 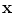 have the same unit norm (since
have the same unit norm (since  ) and consequently the images of all points x in the associated feature space
) and consequently the images of all points x in the associated feature space  lie on the unit sphere.
lie on the unit sphere.
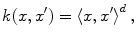
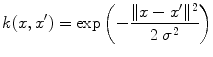
 have the same unit norm (since
have the same unit norm (since 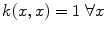 ) and consequently the images of all points x in the associated feature space
) and consequently the images of all points x in the associated feature space 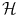 lie on the unit sphere.
lie on the unit sphere.Reproducing kernels as feature maps
One could wonder what is the feature map Φ which was used to build the Gaussian kernel. In fact kernel theory goes far beyond the way we introduced kernels. Let us consider any symmetric function k, not necessarily related to a feature map. Let us suppose also that k, seen as an operator, is positive definite, that is to say that for any non-zero L 2 function 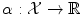 :
:
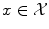 , we need a measure on
, we need a measure on 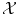 . This measure is often thought of as a probability measure over
. This measure is often thought of as a probability measure over 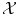 , giving more weight to objects that are more likely to appear.
, giving more weight to objects that are more likely to appear.




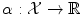 :
: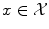 , we need a measure on
, we need a measure on 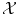 . This measure is often thought of as a probability measure over
. This measure is often thought of as a probability measure over 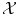 , giving more weight to objects that are more likely to appear.
, giving more weight to objects that are more likely to appear.Then we can define from this kernel k an associated feature map by:
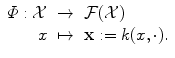
This image of any input x by Φ is the function
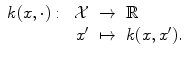
Φ has now values in the space 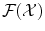 of functions over
of functions over 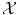 instead of having values in just a finite dimensioned vector space like
instead of having values in just a finite dimensioned vector space like 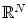 .
.
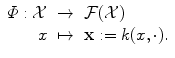
(2)
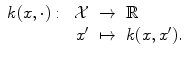
(3)
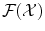 of functions over
of functions over 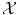 instead of having values in just a finite dimensioned vector space like
instead of having values in just a finite dimensioned vector space like 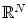 .
.The magic comes from Moore-Aronszajn theorem [2] which states that it is always possible, for any symmetric positive definite function k, to build a reproducing kernel Hilbert space (RKHS) 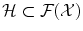 so that
so that
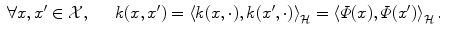
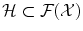 so that
so that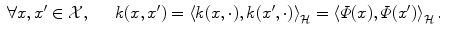
(4)
Because of such a property, symmetric positive definite kernels are also called reproducing kernels. This theorem highlights the duality between reproducing kernels k and feature maps Φ: choosing the feature space or choosing the kernel is equivalent, since one determines the other.
The Gaussian case (details)
We can make explicit the inner product on  in the Gaussian case. The associated norm is
in the Gaussian case. The associated norm is
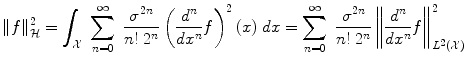 which penalizes all fast variations of f at all derivative orders. We refer to [6] for a more general mathematical study of radial basis functions. Intuitively, consider the operator
which penalizes all fast variations of f at all derivative orders. We refer to [6] for a more general mathematical study of radial basis functions. Intuitively, consider the operator 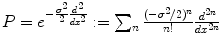 . In the Fourier domain, it writes
. In the Fourier domain, it writes 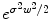 , whereas k(x, ⋅ ) becomes
, whereas k(x, ⋅ ) becomes 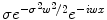 . Thus
. Thus 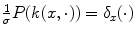 is a Dirac peak in the space
is a Dirac peak in the space 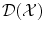 of distributions over
of distributions over 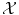 . The inner product
. The inner product 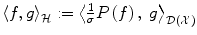 on
on 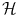 will therefore satisfy:
will therefore satisfy:
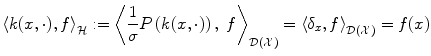 hence, for the particular case
hence, for the particular case 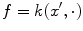 ,
,
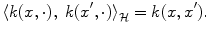
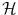 in the Gaussian case. The associated norm is
in the Gaussian case. The associated norm is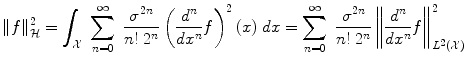
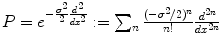 . In the Fourier domain, it writes
. In the Fourier domain, it writes  , whereas k(x, ⋅ ) becomes
, whereas k(x, ⋅ ) becomes 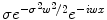 . Thus
. Thus 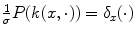 is a Dirac peak in the space
is a Dirac peak in the space 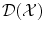 of distributions over
of distributions over 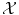 . The inner product
. The inner product 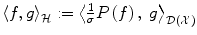 on
on 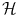 will therefore satisfy:
will therefore satisfy: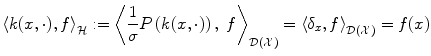
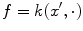 ,
,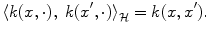
The overfitting problem
The kernel k should be chosen carefully, since it is the core of the generalization process: if the neighborhood induced by k is too small (for instance if k is a Gaussian with a tiny standard deviation σ), then we will overfit the given examples without being able to generalize to new points (which would be found very dissimilar to all examples). On the contrary, if the neighborhood is too large (for instance if k is a Gaussian with a standard deviation so huge that all examples are considered as very similar), then it is not possible to distinguish any clusters or classes.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree