Myocardial Perfusion Cardiovascular Magnetic Resonance: Advanced Techniques

The physiologic basis for and the general principles of myocardial perfusion cardiovascular magnetic resonance (CMR) are covered in detail in other chapters. The key challenge of first-pass dynamic contrast-enhanced acquisition is to capture data with high temporal and spatial resolution during the myocardial contrast passage. The recommended minimal requirements for standard perfusion CMR are to acquire data in three short-axis sections of the heart according to criteria defined by the American Heart Association (AHA) at every R-R interval and with an in-plane spatial resolution of at least 3 × 3 mm. These requirements are most commonly met with saturation recovery fast gradient echo pulse sequences combined with spatial undersampling methods or echo planar imaging to accelerate data acquisition by 2- to 3-fold. The standardized CMR protocols 2013 update by the Society for Cardiovascular Magnetic Resonance (SCMR) recommends a basic technique for perfusion CMR ( Table 5.1 ).

TABLE 5.1

Basic Perfusion CMR Technique

Pulse sequence	Saturation recovery imaging with readout: • Spoiled GRE • GRE-echo planar hybrid • Steady-state free precession
Acceleration method	Parallel imaging, if available
Temporal resolution	Every heartbeat (for ischemia detection)
Readout temporal resolution (= acquisition shot duration)	~100–125 ms or shorter as available
No. of dynamics	Image for 40–50 heartbeats, by which time contrast has passed through the LV myocardium
No. of slices	At least 3 short-axis slices
In-plane spatial resolution	<3 mm
Slice thickness	8 mm
Contrast agent dose and administration regime	0.05–0.1 mmol/kg (3–7 mL/s) followed by at least 30 mL saline flush (3–7 mL/s)
Breath-holding	Breath-hold starts during early phases of contrast infusion before contrast reaches the LV cavity

CMR, Cardiovascular magnetic resonance; GRE, gradient echo; LV, left ventricular.

Advanced Techniques

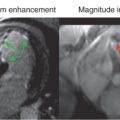
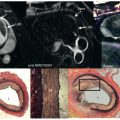
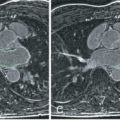
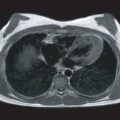
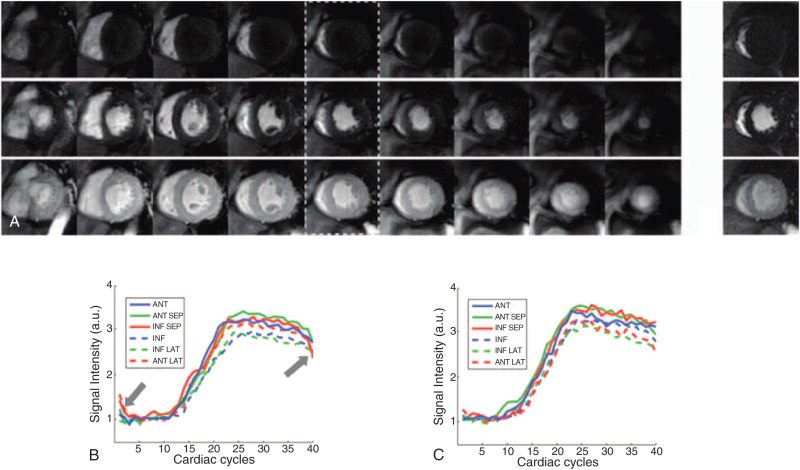
The need for higher spatial and temporal resolution in dynamic CMR has prompted the development of several dedicated imaging speed-up techniques. Effects on signal-to-noise ratio (SNR) and increasing artifacts limit the practically achievable acceleration to approximately 2- to 3-fold using standard acceleration techniques such as echo planar imaging or parallel imaging. However, data acquisition can be further accelerated with methods that exploit both temporal and spatial correlations capitalizing on significant spatiotemporal redundancy within imaging data, which is particularly relevant to first-pass perfusion imaging. Several of these approaches have been used to improve in-plane spatial resolution of myocardial perfusion CMR with reductions in dark rim artifact, better detection of subendocardial ischemia, and possible improvement in diagnostic accuracy versus standard resolution acquisition ( Figs. 5.1 and 5.2 ). Others have used the speed-up to increase spatial coverage through acquisition of more than 3 slices or even whole-heart three-dimensional (3D) acquisition, which allows more reliable calculation of the total myocardial ischemic burden (MIB), akin to nuclear myocardial perfusion imaging (MPI) ( Fig. 5.3 ). An additional benefit of 3D perfusion CMR is that it allows the acquisition of all slices at the same time point in the cardiac cycle—for example, in mid-diastole or end-systole—so that motion artifacts can be reduced and registration between slices improved.

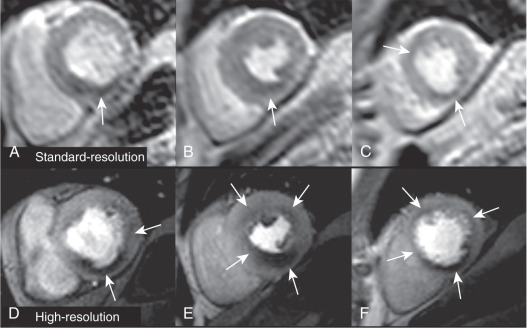
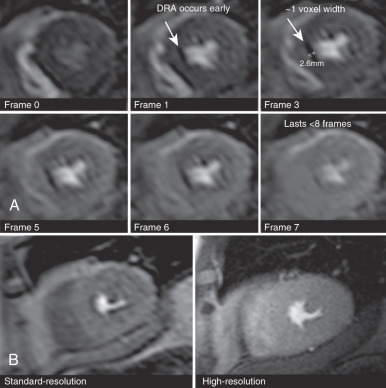
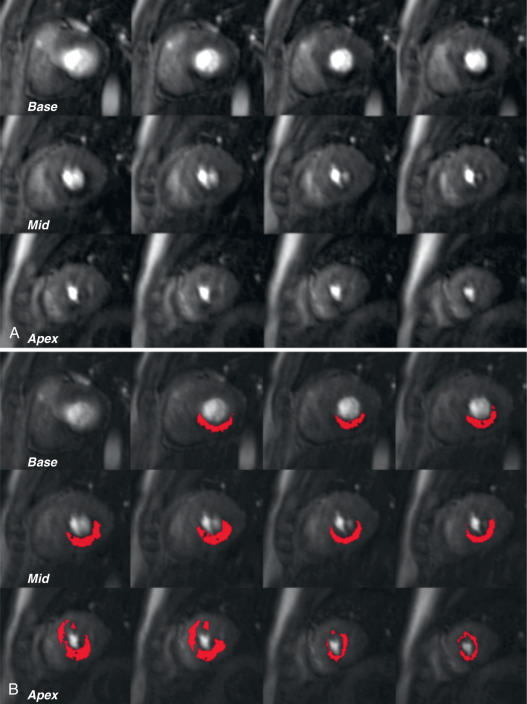
However, although both high-resolution and 3D whole-heart perfusion CMR methods have been shown to be feasible and to have high diagnostic accuracy, most clinical studies to date have had small sample sizes and were conducted in single centers. Furthermore, direct comparison between standard and advanced methods are largely lacking, so that it remains unclear whether their theoretical benefits translate into altered patient management. The more advanced acceleration methods that are needed for high-resolution and 3D perfusion CMR also have specific limitations and are not necessarily available outside of research institutions. This chapter gives a brief overview of the principles of advanced acceleration in perfusion CMR, and summarizes the current evidence for high spatial resolution and 3D whole-heart acquisitions.

Acceleration Methods

Most of the studies reporting high-resolution or 3D perfusion CMR have used techniques based on “prior-knowledge” to derive the required acceleration factors for data acquisition. Prior-knowledge methods are based on the observation that image datasets exhibit considerable correlation in space and time. Perfusion CMR datasets contain a high degree of temporal redundancy, because data are acquired at a single time point in the cardiac cycle using electrocardiogram (ECG)-gating and during breath-holding—this means that most of the image is static and the predominant change between neighboring time frames is related to the passage of contrast. This image redundancy can be taken advantage of by undersampling data in the time (t) domain as well as the more conventional undersampling in the spatial ( k -space) domain. With some of the acceleration schemes discussed later, data acquisition can be accelerated up to a factor of 10 times. This level of acceleration has been used to improve spatial resolution (high-resolution perfusion CMR), increase spatial coverage within a single acquisition shot (3D whole-heart perfusion CMR) or to achieve a mixture of both.

k-t Undersampling Techniques

The k-t broad linear acquisition speed-up technique ( k-t BLAST) is a prior-knowledge spatiotemporal (k-t) undersampling technique that has gained common use. In k-t BLAST, undersampling is applied along k -space and time, while a low spatial resolution image (“training data”) is obtained in an interleaved fashion during the acquisition. A nonaliased, full image series is then reconstructed using prior knowledge derived from the training data ( Fig. 5.4 ). The signal aliasing is resolved by an adaptive filtering process in which the aliased signal is distributed according to a low-resolution estimate of the signal covariance, as derived from the training images. A particular advantage of this approach is that it allows some overlapping of the aliased object, thereby permitting higher acceleration factors. However, the inherent temporal filtering reduces temporal fidelity, which can lead to reconstruction errors or limit the reduction in data acquisition actually achieved.

A further limitation of k-t BLAST is that the reconstruction problem is intrinsically underdetermined (i.e., there are fewer equations than unknowns), which is a reflection of its dependence on the estimated signal covariance from training data. One method of improving this is to incorporate sensitivity encoding information into the reconstruction—this is the k-t SENSE method. A further solution, which allows the use of higher acceleration factors, is to constrain the reconstruction using a standard data compression technique, called principal component analysis (PCA)—this is a commonly used mathematical algorithm that reduces highly dimensional datasets to lower dimensionality by extracting and exploiting relevant correlations within the data. The extension of k-t BLAST or k-t SENSE methods using PCA in the reconstruction is referred to as k-t PCA.

In the k-t PCA method, the adaptive filter used to remove aliasing is improved by applying PCA to the training data from which the filter is derived. Effectively, PCA is used to transform the images into a new mathematical domain of temporal “basis function” more suitable for reconstruction. The advantage of this new mathematical domain is that it is sparser, even in cases of nonperiodic motion such as respiration or misgating, and therefore the core perfusion data is contained within a few principal components and the rest can be discarded. This mathematical transformation process facilitates the easier separation of overlapping signals before they are converted back into images and accounts for the greater temporal fidelity and relative robustness of k-t PCA to motion.

Non-Cartesian Techniques

Alternative approaches to acceleration involve data acquisition along non-Cartesian patterns such as radial trajectories through the center of k -space ( Fig. 5.5 ). Spatial and temporal redundancy are exploited serially and the altered geometry of k -space coverage facilitates greater efficiency compared with conventional Cartesian techniques by collecting more data with each RF excitation. Non-Cartesian techniques can also be combined with parallel imaging techniques and hold potential for large gains in spatial–temporal resolution.

In the highly constrained back-projection reconstruction (HYPR) method and other radial acquisition variants, k -space data is acquired with undersampled radial projections and overall rotation of the undersampling pattern at different time points. In image reconstruction, a fully sampled composite image is formed by populating missing data from neighboring time frames. This very low temporal resolution composite is then used to constrain back projection of the undersampled data acquired for each individual time frame.

To date, perhaps because other approaches are already well established, radial imaging has not been widely applied to two-dimensional (2D) perfusion CMR, other than for specific research purposes such as multiple samples through the center of k -space to calculate the arterial input function (AIF) or to capitalize on its inherent motion robustness for developing free-breathing techniques. Radial sampling does, however, lend itself to combination with compressed sensing methods (see later) and may therefore see greater future application in 3D perfusion CMR techniques requiring particularly high acceleration factors.

Spiral imaging is another non-Cartesian technique in which data is acquired spiraling outward from the central raw data through k -space. Spiral pulse sequences have some inherent efficiency and SNR advantages over the radial technique, but are also more sensitive to off-resonance effects. However, careful selection of readout duration, flip angle strategy, and other sequence characteristics have been shown to compensate for spiral-related artifacts to produce high-quality high-resolution perfusion images. Most commonly, for 3D data acquisition, a stack of spiral planes with Fourier encoding in the third direction is used to achieve whole-heart coverage in a cylindrical distribution ( Fig. 5.6 ).

Compressed Sensing

Non-Cartesian trajectories have reduced cardiac motion-induced dark rim artifact compared with conventional Cartesian acquisition strategies. In addition, the acquisition efficiency and benign aliasing artifacts enable acquisition of higher-resolution images for a given acquisition time. However, both radial and spiral techniques require accurate scanner calibration and special image reconstruction techniques. An alternative method for reconstruction of undersampled data is compressed sensing (CS), which is based upon the principle that an image with a sparse representation in a known transform domain can be recovered from randomly undersampled k -space data using a nonlinear reconstruction ( Fig. 5.7 ). Sparsity in this context describes a matrix of pixels with predominantly zero values in a single image or series of images. CS is therefore readily applicable to perfusion CMR because the signal is sparse in the combined temporal and spatial domain with only portions of the field of view requiring full temporal bandwidth and the other regions having only static information or at low temporal frequencies. The additional CS requirement of incoherence (i.e., that undersampling artifacts look like additive noise) can be achieved in perfusion CMR by randomly omitting phase-encoding lines (k _y) with a different pattern for each time point (t) , generating a random undersampling pattern in k _y-t space. Compared with k _y-only random undersampling, k _y-t random undersampling increases the incoherence, because the undersampling artifacts are incoherently distributed along two dimensions rather than one.

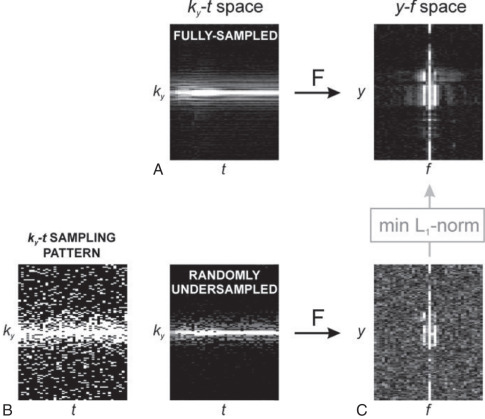
Unlike k-t BLAST and k-t SENSE, CS does not require training data, and, as a result, it may be less sensitive to inconsistencies between training and imaging data. Application of CS to dynamic CMR has been presented in methods such as k-t SPARSE and k-t FOCUSS, using the temporal fast Fourier transform (FFT) as the sparsifying transform, and k _y-t random undersampling. Maximum acceleration rate in CS is determined by image sparsity, and in practice, the number of required samples is approximately three to five times the number of nonzero coefficients in the image. Similar to the other advanced acceleration methods discussed, CS can be combined with parallel imaging techniques when multiple receiver coils are employed to obtain higher accelerations ( Fig. 5.8 ).

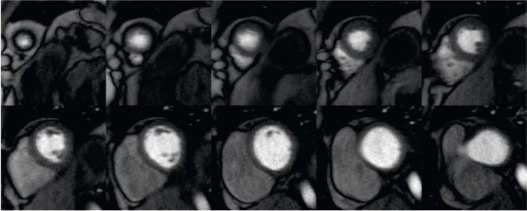
High-Resolution Perfusion Cardiovascular Magnetic Resonance

There is no clear definition of “high-resolution perfusion CMR,” but an in-plane spatial resolution better than 2 mm, which is comparable with that of other common CMR methods such as late gadolinium enhancement (LGE) or cine imaging, is generally considered high. The rationale for pursuing high-resolution CMR is to facilitate comparison with cine and LGE images, to improve the detection of subendocardial ischemia and transmural ischemic gradients, and to reduce dark rim artifacts. These artifacts are a common finding in conventional perfusion CMR and are thought to be caused by magnetic susceptibility effects, Gibbs ringing, and cardiac motion during acquisition. Because these artifacts are directly proportional to voxel size, high-resolution perfusion CMR leads to a reduction of dark rim artifact (see Fig. 5.2 ). As discussed, non-Cartesian sampling techniques such as radial or spiral imaging have shown particular benefits in minimizing dark rim artifact reduction because of their robustness to motion and Gibbs ringing effects.

Methods and Clinical Validation

High-resolution perfusion CMR was first described in a feasibility study using 5-fold k-t SENSE to achieve an in-plane spatial resolution of 1.5 mm. The study reported similar overall image quality as standard-resolution (in-plane spatial resolution: 2.6 mm) SENSE-accelerated acquisition, but there was a significant reduction in the extent of dark rim artifact (mean thickness: 1.7 vs. 2.4 mm; P < .01) and SNR corrected for pixel size was higher for the k – t method. In a subsequent small study by Maredia et al., different tradeoffs between spatial resolution and shot duration were explored and a reduction in dark rim artifact with the highest in-plane spatial resolution was confirmed.

Following the first feasibility studies in volunteers, high-resolution perfusion CMR has been validated in several small patient studies ( Table 5.2 ). Plein et al. used an identical sequence to their previous volunteer study (1.5 T, 5-fold k-t SENSE, in-plane resolution 1.4 mm) in 51 patients with known or suspected coronary artery disease (CAD). High-resolution acquisition was found to have high image quality and a high diagnostic accuracy (area under the curve, AUC: 0.85) compared with quantitative coronary angiography (QCA) with similar performance in single-vessel and multivessel disease (AUC: 0.87 vs. 0.82). Manka et al. used k-t SENSE with 8-fold acceleration at 3 T to achieve an in-plane spatial resolution of 1.1 mm, reporting an AUC of 0.94 in 20 patients with suspected CAD against QCA. Lockie et al. validated high-resolution perfusion CMR (5-fold k-t BLAST, in-plane resolution 1.2 mm) against invasive fractional flow reserve (FFR) and in 42 patients reported a high diagnostic accuracy (AUC: 0.92) for the detection of hemodynamically significant lesions (FFR < 0.75). In a study by Salerno et al., a saturation recovery interleaved variable-density spiral pulse sequence achieving 2 × 2 mm in-plane spatial resolution for three short-axis slices was used in 41 patients listed for QCA. The sensitivity, specificity, and accuracy were 89%, 85%, and 88%, respectively, to detect coronary stenosis >50%. Finally, a variant of the HYPR method known as sliding-window conjugate gradient HYPR (6 contiguous slices, 1.6 mm in-plane spatial resolution), has been shown to be clinically feasible in a single-center study ( n = 50) and demonstrated high diagnostic accuracy (sensitivity 96%, specificity 82%). Radial perfusion CMR has also been shown to be effective in eliminating the need for ECG gating and has the potential to achieve high diagnostic accuracy in arrhythmic patients ( Fig. 5.9 ).

TABLE 5.2

Clinical Validation of Advanced Accelerated Perfusion Cardiovascular Magnetic Resonance

	No.		Advanced Acceleration Method	In-Plane Resolution	Spatial Coverage	Reference Standard	Diagnostic Accuracy
High Resolution
Plein et al. 2008	51	1.5 T	5 × k-t- SENSE	1.4 mm	4 slices (NC) ^b	QCA > 50%	0.85 ^c
Plein et al. 2008	33	1.5 T	5 × k-t SENSE	1.5 mm	4 slices (NC) ^b	QCA > 50%	0.80 ^c
Plein et al. 2008	33	3.0 T	5 × k-t SENSE	1.3 mm	4 slices (NC) ^b	QCA > 50%	0.89 ^c
Manka et al. 2010	20	3.0 T	8 × k-t SENSE	1.1 mm	3 slices (NC)	QCA > 50%	0.94 ^c
Lockie et al. 2011	42	3.0 T	5 × k-t BLAST	1.2 mm	3 slices (NC)	FFR < 0.75	0.92 ^c
Lockie et al. 2011	42	3.0 T	5 × k-t BLAST	1.2 mm	3 slices (NC)	FFR < 0.75	0.89 ^c[MPR] ^a
Motwani et al. 2012	100	1.5 T	8 × k-t BLAST	1.6 mm	3 slices (NC)	QCA ≥ 50%	0.93 ^c
Ma et al. 2012	50	3.0 T	SW-CG-HYPR	1.6 mm	6 slices (WH)	QCA ≥ 50%	0.90 ^d
Chirbiri et al. 2013	67	3.0 T	5 × k-t SENSE	1.2 mm	3 slices (NC)	FFR < 0.80	0.86 ^c[TPG] ^a
Salerno et al. 2014	41	1.5 T	8 × VD Spiral	2.0 mm	3 slices (NC)	QCA > 50%	0.88 ^d
3D
Manka et al. 2011	146	3.0 T	6 × k-t SENSE	2.3 mm	16 slices (WH)	QCA ≥50%	0.83 ^d
Manka et al. 2012	120	1.5 T	10 × k-t PCA	2.0 mm	16 slices (WH)	FFR < 0.75	0.87 ^d
Jogiya et al. 2012	53	3.0 T	10 × k-t PCA	2.3 mm	12 slices (WH)	FFR < 0.75	0.91 ^d
Jogiya et al. 2014	33	3.0 T	10 × k-t PCA	2.3 mm	12 slices (WH)	QCA ≥ 70%	0.88 ^d
Manka et al. 2015	150	3.0 T	10 × k-t PCA	2.3 mm	16 slices (WH)	FFR < 0.80	0.87 ^c
Motwani et al. 2014	20	3.0 T	10 × k-t PCA	2.3 mm	12 slices (WH)	QCA ≥ 70%	0.95 ^b[sMBF] ^a