with A p ∈ {“obj”, “bkg”} can be used to represent the segmentation of P into object (“obj”) and background (“bkg”) voxels. Let N be the set of unordered neighboring pairs {p, q} in set P according to the used neighborhood relation. In our case, a 6-neighborhood relation is used to save memory. The cost of a given graph cut segmentation A is defined as 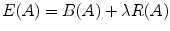 where
where 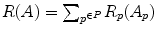 takes region properties into account and
takes region properties into account and 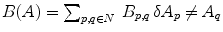 , with
, with 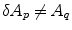 equals 1 if
equals 1 if 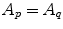 and 0 if
and 0 if 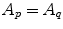 , being boundary properties. The parameter λ with λ ≥ 0 allows to tradeoff the influence of both cost terms. Using the s–t cut algorithm, a partition A can be found which globally minimizes E(A).
, being boundary properties. The parameter λ with λ ≥ 0 allows to tradeoff the influence of both cost terms. Using the s–t cut algorithm, a partition A can be found which globally minimizes E(A).
Region term
The region term R(A) specifies the costs of assigning a voxel to a label based on its gray-value similarity to object and background regions. For this purpose, user defined seed regions are utilized. The region cost R p (·) for a given voxel p is defined for labels “obj” and “bkg” as negative log-likelihoods 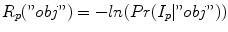 and
and 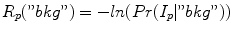 with
with 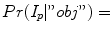
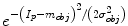 and
and 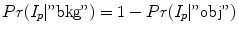 , respectively. From a object seed region placed inside the liver, the mean m obj and standard deviation σ obj are calculated. Clearly, in the above outlined approach, a simplification is made since liver gray-value appearance is usually not homogeneous. However, in combination with the other processing steps this simplification works quite well. Further, the specified object seeds are incorporated as hard constraints, and the boundary of the scene is used as background seeds.
, respectively. From a object seed region placed inside the liver, the mean m obj and standard deviation σ obj are calculated. Clearly, in the above outlined approach, a simplification is made since liver gray-value appearance is usually not homogeneous. However, in combination with the other processing steps this simplification works quite well. Further, the specified object seeds are incorporated as hard constraints, and the boundary of the scene is used as background seeds.
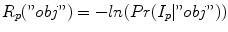 and
and 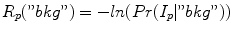 with
with 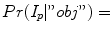
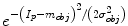 and
and 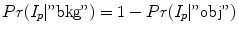 , respectively. From a object seed region placed inside the liver, the mean m obj and standard deviation σ obj are calculated. Clearly, in the above outlined approach, a simplification is made since liver gray-value appearance is usually not homogeneous. However, in combination with the other processing steps this simplification works quite well. Further, the specified object seeds are incorporated as hard constraints, and the boundary of the scene is used as background seeds.
, respectively. From a object seed region placed inside the liver, the mean m obj and standard deviation σ obj are calculated. Clearly, in the above outlined approach, a simplification is made since liver gray-value appearance is usually not homogeneous. However, in combination with the other processing steps this simplification works quite well. Further, the specified object seeds are incorporated as hard constraints, and the boundary of the scene is used as background seeds.Boundary term
The basic idea is to utilize a surfaceness measure as boundary term which is calculated in four steps:
1.
Gradient tensor calculation: First, to reduce the effect of unrelated structures on the gradient, the gray value range of the image is adapted:
Ĩ f = 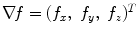 is calculated for each voxel f on the with
is calculated for each voxel f on the with 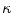 gray-value transformed data volume V by means of Gaussian derivatives with the kernel
gray-value transformed data volume V by means of Gaussian derivatives with the kernel 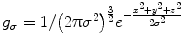 and standard deviation σ. The gradient tensor
and standard deviation σ. The gradient tensor 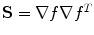 is calculated for each voxel after gray-value transformation.
is calculated for each voxel after gray-value transformation.
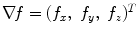 is calculated for each voxel f on the with
is calculated for each voxel f on the with 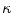 gray-value transformed data volume V by means of Gaussian derivatives with the kernel
gray-value transformed data volume V by means of Gaussian derivatives with the kernel 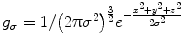 and standard deviation σ. The gradient tensor
and standard deviation σ. The gradient tensor 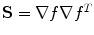 is calculated for each voxel after gray-value transformation.
is calculated for each voxel after gray-value transformation.2.
Spatial non-linear filtering: To enhance weak edges and to reduce false responses, a spatial non-linear averaging of the gradient tensors is applied. The non-linear filter kernel consists of a Gaussian kernel which is modulated by the local gradient vector ∇f. Given a vector x that points from the center of the kernel to any neighboring voxel, the weight for this voxel is calculated as: 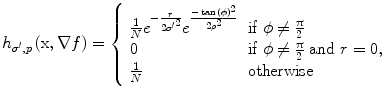 with
with 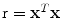 and
and 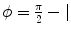 arccos
arccos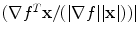 . Parameter ρ determines the strength of orientedness, and σ′ determines the strength of punishment depending on the distance. N is a normalization factor that makes the kernel integrate to unity. The resulting structure tensor is denoted as W.
. Parameter ρ determines the strength of orientedness, and σ′ determines the strength of punishment depending on the distance. N is a normalization factor that makes the kernel integrate to unity. The resulting structure tensor is denoted as W.
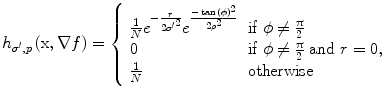 with
with 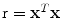 and
and 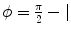 arccos
arccos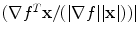 . Parameter ρ determines the strength of orientedness, and σ′ determines the strength of punishment depending on the distance. N is a normalization factor that makes the kernel integrate to unity. The resulting structure tensor is denoted as W.
. Parameter ρ determines the strength of orientedness, and σ′ determines the strength of punishment depending on the distance. N is a normalization factor that makes the kernel integrate to unity. The resulting structure tensor is denoted as W.3.




Surfaceness measure calculation: Let 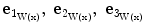 be the eigenvectors and
be the eigenvectors and 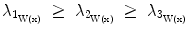 the corresponding eigenvalues of W(x) at position x. If x is located on a plane-like structure, we can observe that
the corresponding eigenvalues of W(x) at position x. If x is located on a plane-like structure, we can observe that 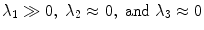 . Thus, we define the surfaceness measure as t(W(x)) =
. Thus, we define the surfaceness measure as t(W(x)) = 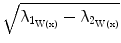 and the direction of the normal vector to the surface is given by
and the direction of the normal vector to the surface is given by 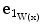 .
.
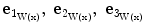 be the eigenvectors and
be the eigenvectors and 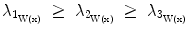 the corresponding eigenvalues of W(x) at position x. If x is located on a plane-like structure, we can observe that
the corresponding eigenvalues of W(x) at position x. If x is located on a plane-like structure, we can observe that 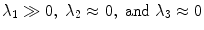 . Thus, we define the surfaceness measure as t(W(x)) =
. Thus, we define the surfaceness measure as t(W(x)) = 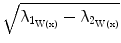 and the direction of the normal vector to the surface is given by
and the direction of the normal vector to the surface is given by 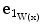 .
.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree