Parallel Imaging: Part 1

80 Parallel Imaging: Part 1

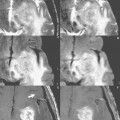
Fig. 80.1

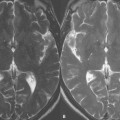
As mentioned in Case 6, one main purpose in the development of multichannel-multicoil systems was to reduce background noise and thus increase SNR without prolonging scan time. This is achieved by limiting the sensitivity of each coil element to a specific region in the volume of interest. The increase in SNR comes from the smaller size of each coil, with resulting higher SNR in close proximity to that coil. Figure 80.1 illustrates the simplest situation in which there are only two coils, one above the abdomen and one below. In a multichannel-multicoil system, the signal from each coil is used to reconstruct an image, as illustrated. These images are then combined to produce the final scan that is presented to the physician for viewing. The entirety of k space is sampled by each coil, symbolically represented in this illustration by a depiction of the data in k space in the center between the two images acquired (one by each coil). In parallel imaging, these so-called phased-array coils are used to reduce scan time while obtaining the same field of view (FOV) and the same spatial resolution, or alternatively (a common clinical application of parallel imaging) to increase resolution while maintaining the same scan time.

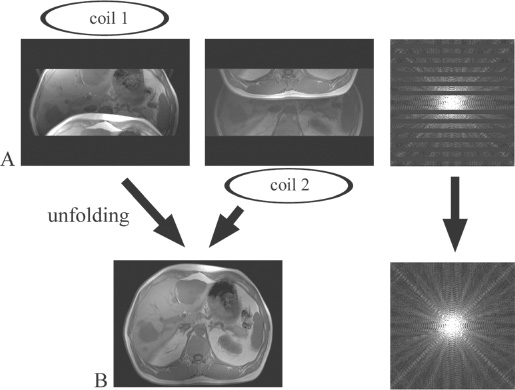
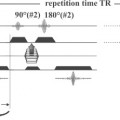
Fig. 80.2

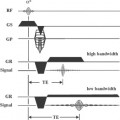
In conventional MR imaging, the scan time and the resolution in the phase-encoding direction are determined in part by the number of phase-encoding steps (e.g., 512 steps or Fourier lines for a 512 × 512 matrix). With parallel imaging, the number of sampled k-space lines and thus scan time are reduced by a factor R (R ≤ number of independent coils in the phase-encoding direction). In the simplest situation, R=2, every other line of k space is sampled. Spatial resolution remains the same because the entire spectrum of k space is still sampled (including in particular the periphery of k space).

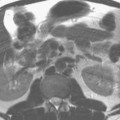
If phase-encoding steps are skipped, or in other words k space is undersampled, the resulting fast Fourier transformation (FFT) is an aliased or “folded” image with a reduced rectangular FOV (Fig. 80.2A). There are two principal ways to create a full FOV. Either the missing k-space lines are calculated and filled in before the FFT and the reconstruction of the image is done as described below (k space-based reconstruction), or the image is “unfolded” after the FFT (image-based reconstruction, described subsequently). Both methods have pros and cons and can be used in virtually every application.

Only gold members can continue reading. Log In or Register to continue