Fig. 10.1
Schematic of the dataflow in a PET system. The detector system consists of a large number of detector modules with associated front-end electronics. The outputs from the detector models are then fed into processing units or detector controllers that determines in which detector element a 511 keV photon interaction occurred. This information is then fed into a coincidence processor, which receives information from all detectors in the system. The coincidence processor determines if two detectors were registering an event within a predetermined time period (i.e., the coincidence time window). If this is the case, a coincidence has been recorded and the information about the two detectors and the time of when the event occurred are saved
In the most recent generation of PET systems, time-of-flight (TOF) information is also recorded. The TOF information that is recorded is the difference in time of arrival or detection of a pair of photons that triggered a coincidence. In the case of a system with infinite time resolution (i.e., there is no uncertainty in time when the detector triggered and the actual time the photon interacted in the detector), the event could be exactly localized to a point along the line connecting the two detectors [3]. This would allow the construction of the activity distribution without the need of an image reconstruction algorithm. However, all detector systems used in modern PET systems have a certain finite time resolution, which translates into an uncertainty in positioning of each event [3]. Currently the fastest detectors available have a time resolution of a few hundred picoseconds, which translates into a positional uncertainty of several centimeters. This time resolution is clearly not good enough to eliminate the need for image reconstruction. However, the TOF information can be used in the image reconstruction to reduce the noise in the reconstructed image. Since systems having TOF capability need to detect events to an accuracy of a few hundred picoseconds, compared to tenths of nanoseconds in conventional PET systems, these systems require a very accurate timing calibration and stable electronics [see Chap. 8 for further details on TOF technology].
10.2.1 Detector Flood Maps
The detector system used in all modern commercial PET systems is based on scintillation detectors coupled to some sort of photodetector readout. One of the most commonly used detector designs is the block detector [4]. In this design, an array of scintillation detector elements is coupled to a smaller number of PMTs, typically four, via a light guide. An example of a block detector is illustrated in Fig. 10.2. The light generated in scintillator following an interaction by a 511 keV photon is distributed between the PMTs in such a way that each detector element produces a unique combination of signal intensities in the four PMTs. To assign the event to a particular detector element, the signals from the PMTs are used to generate two position indices, X pos and Y pos:

where PMTA, PMTB, PMTC, and PMTD are the signals from the four PMTs.

(10.1)
This is similar to the positioning of events in a conventional scintillation camera; however, the X pos and Y pos values do not directly translate into a spatial position or a location of the individual detector elements in the block detector. Each module therefore has to be calibrated to allow an accurate detector element assignment following an interaction of a photon in the detector. The distribution of X pos and Y pos can be visualized if a block detector is exposed to a flood source of 511 keV photons. For each detected event, X pos and Y pos are calculated using an equation [1] and are then histogrammed into a 2-dimensional matrix which can be displayed as a gray-scale image. An example of this is shown in Fig. 10.3. As can be seen in this figure, the distribution of X pos and Y pos is not uniform, but instead the events are clustered around specific positions. These clusters are the X pos and Y pos values that correspond to a specific detector element in the array. As can be seen from the flood image, the location of the clusters does not align on an orthogonal or linear grid. Instead, there is a significant pincushion effect due to the nonlinear light collection versus the position of the detector elements. To identify each element in the detector block, a look-up table is generated based on a flood map like the one shown in Fig. 10.3. First, the centroid of each peak is localized (i.e., one peak for each detector element in the array). Then a region around each peak is generated that will assign the range of X pos and Y pos values to a particular element in the array. During a subsequent acquisition, the values of X pos and Y pos are calculated for each event; then the look-up table is used to assign the event to a specific detector element. Also associated with the positioning, look-up table is an element-specific energy calibration, which will accept or reject the event if it falls within or outside the predefined energy range.



Fig. 10.2
Schematic of a block detector module used in modern PET systems. The array of scintillator detector elements is coupled to the four PMTs via a light guide. The light guide can be integral (i.e., made of the scintillator material) or a non-scintillating material (e.g., glass). The purpose of the light guide is to distribute the light in the detector elements to the four PMTs in such a way that a signal amplitude pattern unique to each detector element is produced. Three examples are illustrated. Top: almost all of the light is channeled to PMTB and almost no light is channeled to the three other PMTs. This uniquely identifies the corner detector. Middle: In the next element over, most of the light is channeled to PMTB and a small amount is channeled to PMTA. By increasing the light detected by PMTA, this allows this scintillator element to be distinguished from the corner element. Bottom: In the central detector element, light is almost equally shared between the PMTB and PMTA, but since the element is closer to PMTB, this signal amplitude will be slightly larger compared to the signal in PMTA. How well the elements can be separated depends on how much light is produced in the scintillator/photon absorption (more light allows better separation). Increasing the number of detector elements in the array makes it more challenging to accurately identify each detector element

Fig. 10.3
The detector elements in a block detector are identified using a flood map. The flood map is generated by exposing the block detector to a relatively uniform flood of 511 keV photons. For each energy-validated detected event, the position indices X pos and Y pos are calculated from the PMT signals (PMTA, PMTB, PMTC, and PMTD). The X pos and Y pos values are histogrammed into a 2-D matrix, which can be displayed as a gray-scale image. The distribution of X pos and Y pos values is not uniform but is instead clustered around specific values, which corresponds to specific detector elements. The peak and the area of X pos and Y pos values around it are then assumed to originate from a specific detector element in the block detector, as illustrated in the figure. From the flood map and the peak identification, a look-up table is generated which rapidly identifies each detector element during an acquisition
To ensure that the incoming events are assigned to the correct detector element, the system has to remain very stable. A small drift in the gain in one or more of the PMTs would cause an imbalance and would affect the locations of the clusters in the flood map. This would in the end result in a misalignment between the calculated X pos and Y pos and the predetermined look-up table [5], which will result in a mispositioning of the events. As will be discussed below, to check gain balance between the tubes is one of the calibration procedures that need to be performed regularly.
10.2.2 Sinogram
The line connecting a pair of detector is referred to as a coincidence line or line of response (LOR). If the pair of detectors is in the same detector ring, this line can be described by a radial offset r from the origin with an angle θ. A set of LORs that all have the same angle (i.e., they are all parallel to each other), but they all have different radial offsets; these then form a projection of the object to be imaged at that angle. For instance, all lines with θ = 0° would produce a lateral projection, whereas all lines with a θ = 90° would produce an anterior-posterior view.
A complete set of projections necessary for image reconstruction would consist a large number of projections collected between 0° and 180°. If all the projections between these angles are organized in a 2-dimensional array, where the 1st dimension is the radial offset r and the 2nd dimension is the projection angle θ, then this arrangement or matrix forms a sinogram, as illustrated in Fig. 10.4. A sinogram is a common method of organizing the projection data prior to image reconstruction. The name sinogram comes from the fact that a single point source located at an off-center position in the field of view (FOV) would trace a sine wave in the sinogram. The visual inspection of a sinogram also turns out to be a very useful and efficient way to identify detector or electronic problems in a system.
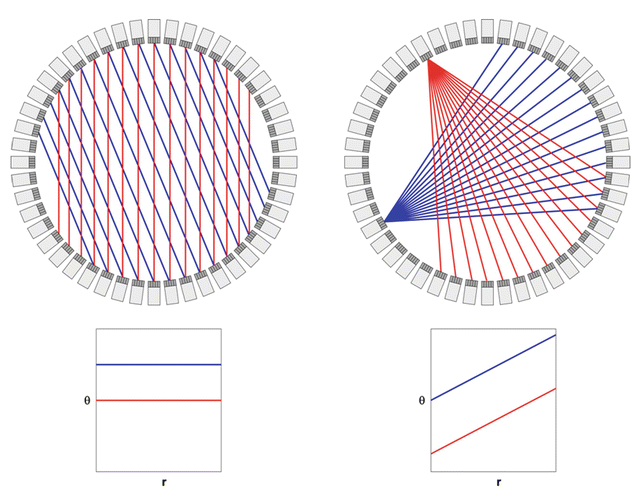

Fig. 10.4
A sinogram is a convenient of histogramming and storing the events along the coincidence lines or LORs in a tomographic study. In its simplest form, a sinogram is a 2-D matrix where the horizontal axis is the radial offset r of a LOR and the vertical axis is the angle θ, of the LOR. If one considers all LOR that are parallel to each other, these would fall along a horizontal line in the sinogram. In the left figure, this is illustrated for two different angles of LOR. If one considers all the coincidences or LOR between one specific detector and the detectors on the opposite side in the detector ring, these will follow a diagonal line in the sinogram, as illustrated in the right figure. The sum of all the counts from the fan of coincidence lines or LOR is sometimes referred to as a fan sum. These fan sums are used in some systems to generate the normalization that corrects for efficiency variations and can also be used to detect drifts and other problems in the detector system. In multi-ring systems, there will be a sinogram for each detector ring combination. In a TOF system each time bin will also have its own sinogram. A sinogram can therefore have up to five dimensions (r, θ, z, ϕ, t) depending on the design of the system
Consider a one particular detector in the system and the coincidence lines it forms with the detectors on the opposite side in the detector ring (Fig. 10.4, right). In a sinogram, this fan of LORs would follow a diagonal line across the width of the FOV. By placing a symmetrical positron emitting source such as a uniform-filled cylinder with 68Ge or 18F, at the center of the FOV of the scanner, all detectors in the system would be exposed to approximately the same photon flux. If all detectors in the system had the same detection efficiency, then each detector would record the same number of counts per second in this source geometry. In this source geometry, the summation of all the coincidences between a particular detector element and its opposing detector element is sometimes referred to as fan sum. The fan sums are used in some systems to derive the normalization correction that is used to correct for efficiency variations between the detector elements in the system. The fan sums can also be used to detect problems in the detector system
Figure 10.5 shows a normal sinogram of a uniform cylinder phantom in a PET system. In addition to the noise originating from the counting statistics, it contains a certain amount of a more structured noise or texture. The observed variation seen in the sinogram is normal and originates primarily from the fact that all detectors in the system do not have the same detection efficiency. There are several additional factors that contribute to this, such as variation in how energy thresholds are set, geometrical differences, differences in physical size of the each detector element, etc. These variations are removed using a procedure that is usually referred to as normalization, which is discussed later in this chapter.


Fig. 10.5
Illustration of how the sinogram can be used to identify detector problems in a PET system. (a) A normal sinogram of a uniform cylinder phantom placed near the center of the FOV of the system. The crosshatch pattern reflects the normal variation in efficiency between the detector elements in the system. (b) The dark diagonal line indicates a failing detector element in the system (no counts generated). (c) The broad dark diagonal line indicates that an entire detector module is failing in. (d) Example of when a detector module is generating random noise. (e) Example of when the receiver or multiplexing board of the signals from a group of the detector modules is failing. (f) Example of problems in the coincidence processing board. In this case, the signals from two groups of opposite detector modules are lost. (g) Example of problems in the histogramming memory, where random numbers are added to the valid coincidences in the sinogram
One thing that is clearly noticeable in the sinogram is the “crosshatch” pattern, which reflects the variation in detection efficiency as discussed above. As mentioned, it is expected to observe a certain amount of normal variation in detection efficiency. This can under most circumstances be calibrated or normalized out as long as the system is stable in there is no drift in the gain of the detector signals. Since a certain amount of electronic drift is inevitable, a normalization calibration needs to be performed at regular intervals. The frequency depends on the manufacturers specifications but can be as frequent as every single day as part of the daily QC or done monthly or quarterly.
If a detector drifts enough or fails, this is typically very apparent by a visual inspection of the sinogram. A detector failure of a PET detector block can either result in that the detector does not respond at all when exposed to a source or that the detector constantly produces event even when no source is present (i.e., noise). The cause of a detector failure could be many, ranging from simple problems such as a loose cable, which usually results in a nonresponding detector, to more complex problems as a faulty PMT, drift in PMT gains, and drift in set energy threshold. The latter issues may result in either a nonresponding detector or that a detector is producing an excessive count rate.
Examples of failing detectors or associated electronics are also illustrated in Fig. 10.5. A failing single detector element in the detector module would appear as a single dark diagonal line in the sinogram (Fig. 10.5b). This problem was fairly common in older PET systems where each detector element was coupled to its own PMT. A common cause of this type of failure was either a failing PMT or the associated electronics (e.g., amplifiers). In the case of a system that uses block detectors, a single dark line may also occur if the detector tuning software had difficulties identifying all detector elements in the detector array. This could be caused by poor coupling of the detector element to the light guide and/or the PMTs or poorly balanced PMTs.
Since the PMTs and associated electronics are shared by many detector elements in block detector, a failure in these components will affect a larger number of detector channels. This is then seen as a wider diagonal band across the sinogram, as illustrated in Fig. 10.5c. Another common detector problem is illustrated in Fig. 10.5d. In this case one of the detectors is generating a large number of random or noise pulses. This could be caused by an energy threshold that is set too low, which, for instance, could be caused by a failing or weak PMT.
As described above, the signals from a larger group of detector blocks are typically multiplexed into what is sometimes referred to as a detector controller. In the case of a failure of the detector controller, the signals from the entire detector group might be lost, which in the sinogram is visualized as an even broader band of missing data (Fig. 10.5e). A problem further downstream in the signal processing chain such as in the electronics determining coincidences may result in a problem illustrated in Fig. 10.5f. Here the signals from two entire detector groups are lost in the coincidence processor, which in this case is seen as a diamond-shaped area in the sinogram. A final example of a hardware failure is shown in Fig. 10.5g. In this case there is a problem with the histogramming system, where random counts are added to the sinogram in addition to the normal data.
There are naturally a large number of variations in other artifacts or patterns in the sinograms that are specific to the design or a particular system, but the sinogram patterns related to the front electronics as described in this section are common for most modern PET systems.
Thus, by a visual inspection of the sinograms from a phantom scan, it is possible to relatively quickly identify whether the system is operational or not. By looking at the patterns in the sinogram, it is also possible to figure out where in the signal chain a problem is occurring. A complete failure is very apparent in the sinogram and makes it easy to make the determination that the system is in need of repair. However, many times there are more subtle problems, such as a slow drift in the system that is not easily detected by visual inspection. Some systems therefore provide a numerical assessment that gives the user some guidance whether the system is operational or not. These tests usually require that the user acquires data of a phantom, such as a 68Ge-filled cylinder every day at the same position in the FOV for a fixed number of counts. The daily QC scan is then compared to a reference scan (e.g., a scan acquired at the time of the most recent calibration or tuning). By comparing the number of counts acquired by each detector module in the QC scan to that in the reference scan, it is possible to determine if a drift has occurred in the system and the system needs to be retuned and recalibrated.
10.3 Detector and System Calibration
The purpose of the detector and system calibration is to make sure that the recorded events are assigned to the correct detector element in the detector module. An energy validation is performed such that only events within a certain energy range are passed on to the subsequent event processing. In addition to positioning and energy calibration of each detector module, each module has to be time calibrated to make sure that coincidence time windows between all detector modules are aligned.
10.3.1 Tube Balancing and Gain Adjustments
As described earlier, the assignment of the events to individual detector elements in the block is based on the comparison of the signal output from the four PMTs. The first step in the calibration of the front-end detector electronics is to adjust the gain of the amplifiers such that the signal amplitude from the four PMTs is on the average and is about the same. This usually entails exposing the detectors to a flood source of 511 keV photons, and the gains are adjusted until an acceptable signal balance is achieved.
Following the tube balancing, detector flood histograms are acquired and generated (as described earlier) to make sure that each detector element in each detector block can be identified. A look-up table is then generated from the flood histogram that is used to assign a particular combination of X pos and Y pos values to a particular detector element.
10.3.2 Energy Calibration
Once all detector elements in the block have been identified, the signal originating from each detector element has to be energy calibrated. Independent of the design of the detector block, it is very likely that signal from each detector element will vary in terms of amplitude, primarily due to differences in light collection by the photodetectors. A detector positioned right above a PMT is very likely to produce a stronger signal compared to a detector located at the edge of a PMT. This is similar to what is observed in conventional scintillation cameras. When comparing energy spectra from the individual elements in a block detector, the location of the photopeak will vary depending on the light collection efficiency of the light.
For the energy calibration, energy spectra are acquired for each detector element, and the calibration software will search for the photopeak in each spectrum. A simple energy calibration is then typically performed where it is assumed that the photopeak corresponds to 511 keV (provided that the source is emitting 511 keV photons and zero amplitude corresponds to zero energy).
10.3.3 Timing Calibration
Coincidence measurements only accept pairs of events that occur within a narrow time window of each other. In order to ensure that most true coincidences are recorded, it is imperative that all detector signals in the system are adjusted to a common reference time. How this is done in practice is dependent of the manufacturer and the system design. The general principle is to acquire timing spectra between all detector modules in the system when a positron emitting source is placed at the center of the system by recording differences in the time of detection of annihilation photon pairs. For a non-calibrated system, the timing spectrum has approximately a Gaussian distribution, centered around an arbitrary time. The distribution around the mean is caused by the timing characteristic of scintillation detectors and the associated electronics and the location of centroid caused by variation in time delays in PMTs, cables, etc. In the timing calibration, this time delay is measured for each detector, and time adjustments are introduced such that the centroid of all timing spectra is aligned. It is around this centroid where the coincidence time window is placed. For non-TOF PET systems, the timing calibration has to be calibrated to an accuracy of around a few nanoseconds. For TOF system, the calibration has to be accurate to below 100 picoseconds.
A modern PET system consists of several tens of thousands of detector elements and requires very accurate and precise calibration. The outcome of the calibration steps many times depends on each other and some of the processes are iterative. Due to the complexity of the system, manufacturers have developed highly automated procedures for these calibration steps. It used to be that a trained on-site physicist or engineer had access to the manufacturer’s calibration utilities, which allowed recalibration or retuning of parts or the entire system. However, in recent years the general trend among manufacturers is that the user does not have access to the calibration utilities, and these tasks are only performed by the manufacturer’s service engineers. Fortunately, PET scanners today are very stable, and the need for recalibration and retuning is far less compared to systems that were manufactured 10–20 years ago.
10.3.4 System Normalization
After a full calibration of the detectors in a PET system, there will be a significant residual variation in both intrinsic and coincidence detection efficiency of the detector elements. There are several reasons for this, such as imperfections in the calibration procedures, geometrical efficiency variations, imperfections in manufacturing, etc. These residual efficiency variations need to be calibrated out to avoid the introduction of image artifacts. This process is analogous to the high-count flood calibration used in SPECT imaging to remove small residual variation in flood-field uniformity. In PET this process is usually referred to as the normalization, and the end result is usually a multiplicative correction matrix that is applied to the acquired sonograms as illustrated in Fig. 10.6. The effects of the normalization on the sinogram and the reconstruction of uniform cylinder phantom are shown in Fig. 10.6. If the normalization is not applied, there is a subtle but noticeable artifact in the image such as the ring artifacts and the cold spot in the middle of the phantom. The origin of the ring artifacts comes from a repetitive pattern in detection efficiency variation across the face of the block detector modules, where the detectors in the center have a higher detections efficiency compared to the edge detectors. Once the normalization is applied, these artifacts are greatly reduced. It should also be noted that the normalization is a volumetric correction as can be noted by the removal of the “zebra” pattern in the axial direction when the normalization is applied (Fig. 10.6).


Fig. 10.6
1st row: The sinogram to the left is a normal uncorrected sinogram of a uniform cylinder phantom. The crosshatch pattern reflects the normal variation in efficiency between the detector elements in the system. The normalization matrix (middle), which is multiplicative, corrects for this and produces a corrected sinogram (right), where the efficiency variations have been greatly reduced. 2nd row: Illustration of the effect of the normalization in the axial direction of the system. The efficiency variation is typically greater in the z-direction compared to the in-plane variation. 3rd and 4th rows: Illustration of the effect of the normalization on a reconstructed image. The transaxial image to the left in the 3rd row shows ring artifacts due to the lack of normalization. These are eliminated when the normalization is applied (right image). The axial cross section of the reconstructed cylinder in the 4th row reflects the efficiency variation axially in a “zebra pattern” when the normalization is not applied (left image). These artifacts are greatly reduced when the normalization is applied (right)
Normalization is usually performed after a detector calibration. There are several approaches on how to acquire the normalization. The most straightforward method is to place a plane source filled with a long-lived positron emitting isotope, such as 68Ge in the center of the FOV. This allows a direct measurement of the detection efficiencies of the LORs that are approximately perpendicular to the source [6]. The source typically has to be rotated to several angular positions in the FOV to measure the efficiency factors for all detector pairs in the system. However, there are several drawbacks of this method. First of all, it is very time consuming to acquire enough counts at each angular position to ensure that the emission data are not contaminated with statistical noise from the normalization. This problem can to a certain degree be alleviated by the use of variance-reducing data processing methods [7].
The most common method for determining the normalization is the component-based method [8, 9]. This method is based on the combination of efficiency factors that are less likely to change over time, such as geometrical factors and other factors that are expected to change over time due to drifts in detector efficiency or due to settings of energy thresholds. This method typically only requires a single measurement that estimates the individual detector efficiency. This is usually done with a uniform cylinder phantom placed at the center of the FOV. The measured detector efficiencies are then combined with the factory-determined factors to generate the final normalization
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree