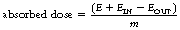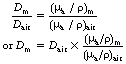In recent years, the term ‘exposure’ has fallen out of common usage and has been replaced by absorbed dose in air or air kerma (the initials of kerma stand for kinetic energy released per unit mass of absorber); for instance, the maximum permissible radiation leakage rate from the X-ray tube is now quoted in air kerma. The main reason for this is that it is much easier to calculate the absorbed dose in a structure from the air kerma.

The measurement of the quantity of electrical charge produced in air by ionization is not the same as the measurement of the energy actually absorbed, although the two quantities are proportional to each other. The energy absorbed by unit mass of the medium is stated as the absorbed dose and is defined thus:

The unit of absorbed dose is the gray (Gy) and so we can say that l gray=1 joule per kilogram (1 Gy=1 J.kg⁻¹).

Note that exposure is defined in terms of X or gamma radiation only, while absorbed dose is defined in terms of any ionizing radiation. Therefore, the absorbed dose from alpha-particles, beta-particles and neutrons are all measured in grays. However, ultraviolet radiation is only capable of excitation rather than ionization of the atoms of the medium and so is outside the scope of the definition of absorbed dose.

If all the electrons produced by the primary and secondary ionizations within a medium are stopped within it, then it can be seen that the energy removed from the beam of ionizing radiation is the same as the energy absorbed by the medium (this makes the assumption that all the fluorescent or characteristic radiation is absorbed, as is the case in body tissues). This does not necessarily apply to a very small volume within the medium – such a volume may be removing energy from the beam but the absorbed energy may be deposited outside the volume (but still within the body) due to the distance travelled by the electrons before coming to rest. Electrons with an energy of 1 MeV travel for about 5 mm in tissue before coming to rest.

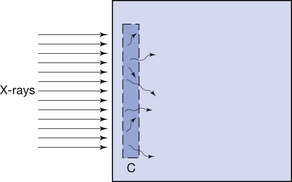
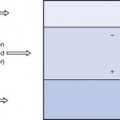
This effect is illustrated in Figure 27.1 (See page 199). Here an incoming X-ray beam of high energy interacts with a volume element V within the medium. Because of the high energy of the beam, the electrons produced by Compton scatter are scattered in a forward direction, so much of their energy is absorbed outside the volume V. There will also be secondary ionizations resulting in the production of delta rays, but for simplicity these are not shown in the figure. In general, if the secondary electrons produced within the volume deposit a total energy E within the medium, and E_IN and E_OUT are the total energies of the electrons entering and escaping from the volume, then the absorbed dose in grays is given by:

Figure 27.1 X-rays interacting with atoms in volume V produce electrons that may travel outside V.

Equation 27.1

where m is the mass of the particular small volume considered. If a larger volume is considered, then this formula can be used to calculate the average absorbed dose in that volume.

Electronic equilibrium is said to occur if E_IN=E_OUT, since there is no net loss or gain of the electrons over the small volume being considered. If E_IN=E_OUT is a constant value not equal to zero, there is said to be quasielectronic equilibrium. If the intensity of the radiation is varied, the net loss or gain of electrons will vary in proportion. An example of electronic equilibrium occurs in the free-air ionization chamber, which will be discussed later in Section 27.5.2.

The absorbed dose expresses the quantity of energy absorbed in the medium due to a beam of ionizing radiation passing through it. As stated at the beginning of this section, the site of the attenuating events (e.g. photoelectric absorption) may be at some distance from the absorption process because of the distance travelled by the ejected electrons before coming to rest. The quantity which measures the amount of attenuation in a small volume is called the kerma (see Sect. 27.3.1).

Kerma is also measured in grays and may differ significantly from the absorbed dose at any particular position within the medium.

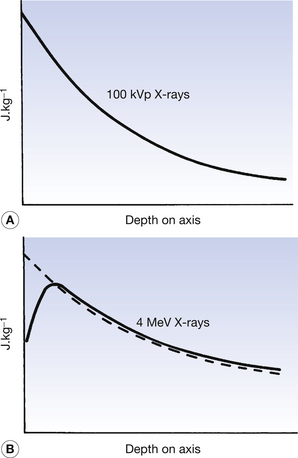
The absorbed dose and kerma along the axis of a beam of X radiation are shown in Figure 27.2. Figure 27.2A shows the case where an X-ray beam generated at 100 kVp is incident upon soft tissue: this type of situation might occur in diagnostic radiography. The electrons released in the primary and secondary ionizations are of relatively low energy and so are absorbed close to the site of the initial attenuating interactions. The kerma and absorbed dose at any particular point along the beam axis are essentially the same and the curves are coincident in the figure. This is not the case if the X-ray beam has high photon energy, since electrons produced by the initial ionization have considerable energy and so deposit their energy some distance from the point of the original attenuation process. As can be seen in Figure 27.2B, the kerma and the absorbed dose due to 4 MeV X-rays interacting with tissue are not the same. It may be easier to understand these curves if it is remembered that:

Figure 27.2 Kerma (dashed line) and absorbed dose for (A) 100 kVp diagnostic beam and (B) 4 MeV therapy beam. In (A) the two curves are coincident, but they are different in (B) because of the increased energy – and hence range – of the secondary electrons produced.

Instruments that are used to measure absorbed dose or absorbed dose rate are called dosimeters and dose-rate meters respectively. Some of these instruments are described in more detail in later sections of this chapter (see Sect. 27.5 onwards). It is common practice to calibrate these meters to read the absorbed dose or dose rate in air through which the X- or gamma-rays are passing. Such a dosimeter may read 0.5 mGy as the total absorbed dose in air at a point within an X-ray beam. It must not be inferred, however, that this is the absorbed dose that would bereceived by any other medium if placed in the same position. For two media to receive the same absorbed dose, each must absorb the same energy from the beam per unit mass (remember, 1 Gy=1 J.kg⁻¹⁾. This is the same as saying that the mass absorption coefficient of the two media must be equal. Thus, if D_air is the absorbed dose in air and D_m the absorbed dose in a medium when both are irradiated with the same beam of X-rays, it follows that if the mass absorption coefficients are not equal, this equation may by drawn up:

Equation 27.2

If the mass absorption coefficient of air and the given medium are known at the energy of the X-ray quanta, the absorbed dose in the medium may be calculated using Equation 27.2. In practice, this allows us to measure the absorbed dose in air at a certain point and then calculate the absorbed dose in the patient at the same point without subjecting the patient to a great degree of discomfort.

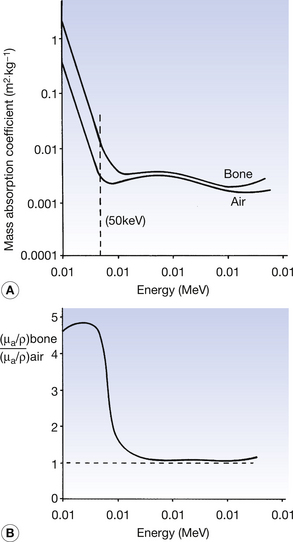
The mass absorption coefficients of both air and bone vary with photon energy. These variations of the two coefficients are shown in Figure 27.3A and the variations in the ratio of the two coefficients are shown in Figure 27 3B. As can be seen from the graphs, at low photon energies (50 keV is shown with the broken line in Figure 27.3A), the mass absorption coefficient of bone is considerably higher than that of air. This is because at low energies the photoelectric effect predominates (τ/ρ ∝ Z³/E³) and the atomic number of bone (Z=14) is approximately double that of air (Z=7.64). For this reason and because of the large difference in density, we get a high level of contrast between bone and air on a radiograph (this can be seen on the chest radiograph or on radiographs of the paranasal sinuses). At an energy of about 1 MeV, however, the two graphs are very close and the ratio of the two coefficients approaches 1. This is because of the dominance of Compton scatter in this region (σ/ρ ∝ electron density and the electron density for bone and air is approximately the same). This means that there would be a low level of contrast between the two if they were radiographed using 1-MeV photons. At above about 10 MeV the curves again diverge owing to the greater amount of pair production in bone compared to air ((π/ρ ∝ Z). Thus, it is clear that an instrument calibrated to read absorbed dose in air must be used with caution when calculating the absorbed dose in another medium as the relationships between the absorption coefficients vary with the photon energies. This is particularly the case in the diagnostic range of energies where absorption is principally by the photoelectric effect, which is very sensitive to both atomic number and photon energy.

Figure 27.3 The variation of energy of (A) the mass attenuation coefficients of air and bone and (B) the ratio of the two coefficients.