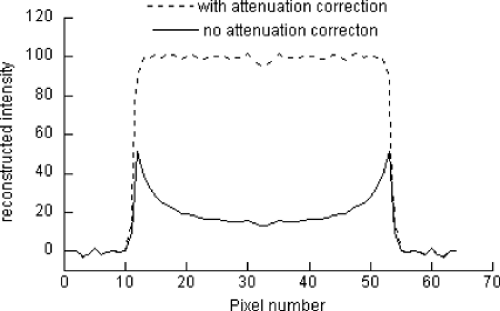
In most instances, attenuation has the greatest impact on SPECT quantitation and can result in order-of-magnitude errors if left uncorrected (4). This can be illustrated with the simple example of a point source at the center of a water-filled cylinder. For a 15-cm radius cylinder, the fraction of emissions (technetium 99m [^99mTc]) not affected by attenuation is e^{(-μ × 15)}, where μ is the linear attenuation coefficient of water at 140 keV, or 0.151/cm. Thus attenuation results in almost a 90% decrease in reconstructed intensity at that point. For distributed sources, the effect is more complicated to analyze but can be illustrated with a slightly more complicated example: a uniform source distribution within the same cylinder. In this case, a profile through the resulting reconstructed image with and without attenuation correction is shown in Figure 12.1. As the figure shows, the reconstructed intensity without attenuation correction is erroneously small throughout the image but particularly so near the center of the cylinder. In more complicated (and more realistic) situations in which the body has nonuniform attenuating characteristics, more complicated artifacts result. The general trend still holds, however: deeper features are affected more by attenuation. Attenuation-correction methods are addressed later.

Scatter effects are more difficult to analyze than attenuation effects, but they are much smaller in magnitude. Typically, scatter results in an approximate 30% increase in detected counts compared with an idealized case in which scatter was excluded. This percentage will vary with the size of the attenuating medium. Many scatter-correction methods have been proposed for SPECT. The methods vary greatly in the extent of physical modeling that is used; however, a relatively simple method has been shown to reduce scatter effects effectively (2). The method uses data acquired within a second, lower-energy window. These “scatter” data, after appropriate scaling, are assumed to represent the scatter component of the primary energy window data and are subtracted from the primary energy window data. Because this method uses two energy windows, it is often referred to as the “dual-energy window method.”

Detector response, or finite spatial resolution, becomes an increasingly important factor in SPECT quantitation as the image feature size decreases. It is observed that for features smaller than approximately twice the spatial resolution of
the detector, the measured activity concentration decreases with the volume of the feature (3). The reason for this effect is that the detected counts in the SPECT image are spread across a larger region than that occupied by the emission source. Thus the measured concentration is necessarily reduced (see also Chapter 11). For larger sources, the spreading of counts away from a point in the SPECT image is balanced by the spreading into the point from surrounding areas of activity. Effective methods for detector-response correction involve linear deconvolution filtering with, for example, Wiener or Metz filters. An example of a Metz filter is shown in Figure 12.2. The filter exceeds unity gain at low spatial frequencies to deconvolve, or sharpen, the detector response blurring. The filter “rolls-off” to zero gain at high frequencies to control high-frequency image noise.