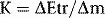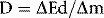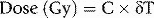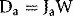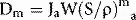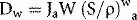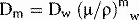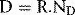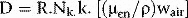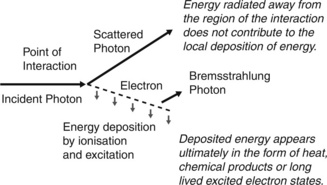
Chapter 2 described the various processes by which photons interact with matter. These interactions produce charged particles (electrons and possibly positrons) which then travel through matter, losing energy by collision processes (ionization and excitation of atoms) and through radiative processes (production of bremsstrahlung), as illustrated in Figure 3.1.

Figure 3.1 Schematic diagram of energy deposition arising from Compton interaction in a matter.

For photon beams, the transfer of energy from radiation to matter may be seen in two distinct stages:

1. transfer of energy from the radiation to emitted charged particles

2. deposition of energy by the emitted charged particles through collision processes.

The first stage is governed by the interaction coefficients for photons in matter as discussed in Chapter 2. The second stage is dependent upon the energies of the emitted charged particles and their subsequent patterns of energy deposition as determined by their stopping powers. Together, these determine the differences in deposition of energy for differing photon energies and materials. For charged particle beams only the second stage is relevant.

Kerma

The term kerma, an acronym for the kinetic energy released per unit mass, is used to quantify the first of the above stages. It is defined by ICRU (1) as:

where Etr represents the energy transferred from photons to charged particles and is the sum of initial kinetic energies of all the charged particles liberated by uncharged ionizing radiation from an amount of material of mass m.

It may be seen from Figure 3.1 that for the Compton interaction illustrated:

1. the energy of an incident photon is shared between a scattered photon and the ejected electron. The scattered photon carries its energy away from the immediate region of the interaction. The term terma represents the total energy removed from the beam per unit mass of matter, including that given to the charged particles and that scattered as photons. Terma is therefore always greater than kerma

2. the electron travels through matter losing energy continually until its kinetic energy is exhausted

3. the travelling electron may lose some energy by bremsstrahlung, producing photons which, like the scattered photon, carry energy away from the immediate vicinity. The term collision kerma refers to that proportion of kerma that is deposited via collision processes only. Kerma and collision kerma differ only in accounting for the energy that is re-radiated. In body tissues, the energy re-radiated is small, being less than 1%, so these two quantities are almost equal.

Absorbed dose

The travelling electrons deposit energy in matter through which they pass, and so the energy deposited by these electrons is displaced in distance from the site of initial transfer of energy from the photon beam. The amount of energy deposited in a small mass of the material is termed the absorbed dose, which is defined by ICRU [1] as:

where Ed is the total energy deposited by these charged particles in a volume element of mass m.

The absorbed dose is similar in value to collision kerma, but displaced due to the motion of the secondary charged particles. Absorbed dose equals collision kerma if one of two conditions are met:

1. the distance travelled by secondary charged particles is sufficiently small for it to be neglected, such that energy may be considered to be absorbed by the matter at the point where it is transferred from photons to the charged particles – a condition known as point deposition of dose. This occurs for low energy photons, where the emitted electrons can travel only short distances, as detailed in Chapter 2

2. the energy lost from the region of initial transfer by the movement of charged particles away from that region is exactly compensated for by energy brought into the region by other travelling electrons produced elsewhere – a condition known as energy equilibrium, or more generally as charged particle equilibrium.

Units of kerma and dose

Both kerma and absorbed dose have units of energy per unit mass, the units for which are joules (J) and kilograms (kg), respectively. The gray is used for both absorbed dose and kerma and is defined as:

Neither absorbed dose nor kerma are material specific and can therefore be related to any matter: a subscript is generally used to indicate the material. Hence K_a and K_w may be used to refer to air kerma and water kerma, respectively. Similarly for absorbed dose.

Measurement and standardization of dose

We have seen that when photons interact in matter, an energy pathway is initiated by which energy is transferred to the matter via emission of charged particles which cause ionization and excitation of atoms of the matter. The energy is eventually manifest as heat or as some form of internal potential energy of electrons and atoms within the matter (e.g. chemical bonds, raised electron energy levels).

Systems of detecting radiation utilize specific parts of this energy pathway. Some systems seek to determine energy deposited in matter by measuring the temperature rise (termed calorimetry). Other detection systems look at chemical changes generated by irradiation of the matter (chemical dosimetry), or utilize long-lived excited electron states (e.g. thermoluminescent dosimetry). Still other systems measure the ionization produced by the charged particles in order to calculate the energy transferred to those particles (ionization chamber dosimetry).

This section describes the systems adopted for the measurement and standardization of absorbed dose that underpin clinical practice. Later sections consider other methods of radiation detection and measurement, including other systems for measuring absorbed dose.

Dose standards

It is of particular importance in radiotherapy to ensure that a dose of radiation delivered in any one treatment centre is consistent over time and is consistent also with that delivered in other centre, this being a central part of ongoing quality control. It also allows direct comparison of treatment techniques and results between centre and is essential for multicentre clinical trials to be effective. Consistency of measurements on a national or international basis is achieved through a process of central standardization, with all measurements being traceable to an accepted national or international standard. The National Standards Laboratory (i.e. the National Physical Laboratory, NPL in the UK) houses the instruments that are used to determine the national standard for absorbed dose measurement. These instruments are purely laboratory instruments that are impractical for routine use within radiotherapy departments.

The UK national standard instruments for the standardization of absorbed dose are of two types:

1. calorimeters for megavoltage photon and electron beams. Calorimeters are used to provide direct determination of absorbed dose [2]

2. free-air ionization chambers for lower energy photon beams from x-ray generators operating at up to 300 kV [3, 4]. These provide direct determination of air kerma from which the absorbed dose to water can be calculated.

Traceability of measurement

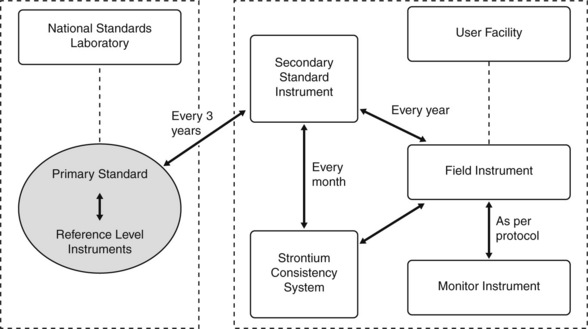
In order to ensure consistency of dose measurement between centre, it is necessary for measurements to be traceable back to the appropriate national standard. This is achieved through a hierarchical arrangement shown schematically in Figure 3.2. Dose measuring instruments within individual hospitals (the field instruments) are used to measure the radiation beams of radiotherapy treatment units. These are calibrated periodically (i.e. annually in the UK) against a secondary standard instrument. The secondary standard instruments are reserved solely for this purpose and are not used to make routine beam measurements. Guidelines on the choice of dosimeter systems for use as secondary standard instruments have been produced by IPEM [5]. Each secondary standard instrument is calibrated periodically (i.e. every 3 years in the UK) by the Standards Laboratory by comparing the response against national reference level instruments that are in turn compared annually with the national standard instrument. The national standards are themselves compared at intervals with equivalent standard instruments developed by standards laboratories in other countries.

Figure 3.2 Traceability to the National Standard is assured through a chain of intercomparisons, some of which are carried out at the National Standards Laboratory and others are carried out in local radiation beams. Between intercomparisons, calibration is assured using a consistency system.

Radiotherapy treatment units, such as linear accelerators and kV therapy units, have in-built dose measuring instruments that monitor and determine the amount of dose delivered – these instruments are known as monitor chambers. Field instruments are used to calibrate these monitor chambers so that each monitor unit delivers a known amount of radiation. These field instruments may be used to determine not only the amount of radiation delivered, but also the pattern of deposition of energy within matter by measuring dose at different points within the matter. They may be used also to calibrate other dose measuring equipment designed for special purpose measurements, such as in-vivo dosimeters.

For the transfer of calibration from instrument to instrument down the chain to be reliable, the method of calibration must be strictly controlled. This is achieved by the adoption of calibration protocols which specify:

• the basis for the standard dose measurement

• the instrumentation and methods for transfer of dose to field instruments by a series of intercomparisons, including specification of any equipment used and any conditions that must exist for the intercomparison to be reliable

• instructions for use of the calibrated dosimeter in routine practice.

Each protocol is specific for an energy range and type of radiation: the protocols for calibration of field instruments are covered in a later section.

Standard calorimeter

In situations where all the absorbed energy is manifest solely as heat, i.e. no energy is ‘lost’ to form new chemicals or stored in excited electron states, the relationship between radiation dose and change in temperature is given by:

where C is the specific heat of the irradiated matter (the amount of energy needed to raise the temperature of unit mass of a substance through 1 degree, expressed in units of in J.kg⁻¹.°C⁻¹) and δT is the change in temperature in degrees Celsius. The equation above assumes no loss of heat to the surrounding environment or structures. Note that the specific heat may also be expressed in calories rather than joules, in which case an additional numerical multiplier of 4.18 is necessary in the above equation.

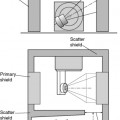
The rise in temperature is extremely small – e.g. a beam of x-rays delivering a dose of 5 Gy to soft tissue causes a temperature rise of only 10^–3°C. Such a small rise in temperature is very difficult to measure accurately and extreme precautions are necessary to prevent heat loss outside the irradiated vessel.

The national standard calorimeter is based on the irradiation of a known mass of graphite (the core of the NPL high energy photon calorimeter measures approximately 20 mm diameter by 3 mm thick) within a graphite phantom. The design of the calorimeter, a photograph and schematic drawing of which are shown in Figure 3.3, has the core shielded by three jackets, each separated by vacuum in order to minimize heat loss. Temperature measurements are carried out using thermistors embedded in the graphite core, the resistances of which change with temperature. In practice, since the amount of heat energy lost from the core to surrounding structures is not negligible and may be difficult to determine, the rise in temperature resulting from irradiation is compared with the rise in temperature produced by heating the core using a known amount of electrical energy, allowing absorbed dose to be determined directly instead of using the above equation.

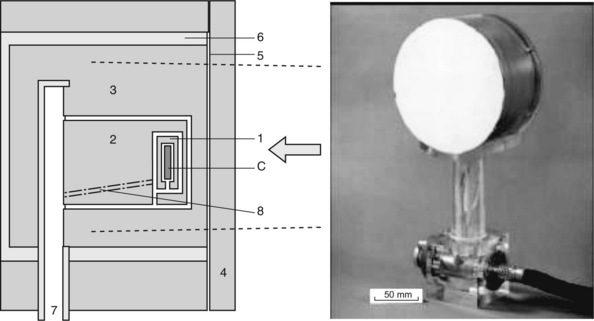
Figure 3.3 Photograph and simplified schematic drawing (redrawn from [2]) of the national standard high energy photon calorimeter, showing the graphite core (C) surrounded by three insulating graphite jackets (1, 2 &. 3). The entire device is housed within a Perspex evacuation vessel (6) which has a thin aluminized mylar front window (5) and which is evacuated via a port (7). A plate (4) suitable for the energy to be measured can be added to the front face. Electrical connections to the core pass through the device (8).

Graphite has the advantage of having no chemical defect (i.e. all the absorbed energy appears as heat) and a specific heat that is one-fifth that of soft tissue or water, thereby producing greater changes in temperature per unit dose. The absorbed dose to water may be calculated from the absorbed dose to graphite using the correction factors determined by Nutbrown [6].

Measurement by calorimetry is largely independent of whether the radiation is delivered continuously or in pulses and of the pulse intensity. It is therefore ideal for measuring radiation from constant-output sources, such as cobalt units, as well as pulsed output from linear accelerators. The pattern of temperature rise (from irradiation) and fall (from leakage of heat away from the core) may be used to determine both the peak and mean dose rates for pulsed radiation sources.

As the standard calorimeter cannot be used in a water tank, a number of specially constructed ionization chambers termed ‘reference standard instruments’ are calibrated annually against the graphite calorimeter in a common graphite phantom. These reference instruments are then used to calibrate in turn the secondary standard instruments using a water phantom. The calibration factor provided for each secondary standard instrument is specific to a stated beam quality and depth of measurement, the latter being important as the spectral content of a radiation beam changes with depth. Table 3.1 shows those photon beam qualities at which calibration factors based on absorbed dose to water as determined by the standard graphite calorimeter are provided by the National Physical Laboratory, UK [7, 8]. When used as a basis for calibration in a radiation beam in the user’s department, the beam quality for that beam must be determined and the appropriate calibration factor obtained by interpolating from the results provided by the standards laboratory. Calibrations in megavoltage photon beams are carried out at the depths shown in Table 3.1 which are beyond the range of contaminating electrons in the radiation beam that have been ejected from the head of the treatment machine [9].

Table 3.1 Photon beam qualities used for therapy level absorbed dose to water calibrations

Beam quality (TPR_20/10)	Equivalent beam energy	Reference depth (cm)
0.568	60 Co	5
0.621	4 MV	5
0.670	6 MV	5
0.717	8 MV	5
0.746	10 MV	5
0.758	12 MV	7
0.779	16 MV	7
0.790	19 MV	7

The quantity TPR_20/10 is the ratio of tissue-phantom ratios at depths of 20 cm and 10 cm respectively, used by Standards Laboratories as the specifier of beam quality (see Chapter 2).

A number of Standards Laboratories have developed water calorimeters that directly measure the rise in temperature of a known mass of water. These avoid uncertainties with the national standard instrument in moving from a graphite phantom to a water phantom. Such instruments have been used to confirm doses specified using other systems of dosimetry for photon and charged particle beams and are being increasingly developed as national dosimetry standards [44–48]

The free air chamber

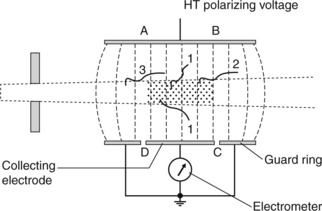
The free air chamber is the primary standard instrument for kV beams, and is shown schematically in Figure 3.4. The free air chamber effectively determines the energy transferred to secondary electrons as a result of interactions of a photon beam within a defined mass of air, i.e. air kerma (k_a).

Figure 3.4 The free air ionization chamber. Irradiation of the mass of air shown shaded, defined by the cross-sectional area of the radiation beam and the length of the collecting electrode, results in emission of electrons that lose their kinetic energy by ionization of air. Those ions created within the region ABCD are collected and measured.

A well-defined beam of radiation, confined by external collimators, is incident upon a volume of air located between metal plates that act as electrodes. The radiation causes ionization of the air, resulting in electrons being ejected. These electrons in turn cause further excitation and ionization as they interact with air molecules: the electrons lose kinetic energy with each interaction and will travel an irregular, tortuous path until they come to rest. Each ejected Compton- or photo-electron can produce several hundred ion pairs. An essential requirement of the free air chamber is that the electrons produced by photon interactions lose all their kinetic energy in air and do not reach the metal electrodes. This requirement determines the minimum separation between the metal electrodes, and the overall size of the chamber. For example, measurement of x-rays generated at 200 kV will require a separation of at least 20 cm.

A potential difference, the polarizing voltage, is applied between the metal electrodes. This causes positively and negatively charged ions produced in the air to separate, such that positive ions will move towards the negative potential plate while electrons will move towards the other. All ions of one charge sign are collected on one electrode, termed the collecting electrode. The charge reaching this electrode is measured and, from this, the number of ions produced may be calculated, since the charge carried by each electron is constant (equal to 1.602×10⁻¹⁹ coulomb). The average energy expended by electrons in creating an ion pair, that is allowing for energy lost in exciting atoms as well as energy lost in ionizing them, is well determined from experimental work. Hence, since the number of ions may be determined using the free air chamber and the average energy necessary to produce each one is known, the total energy transferred to secondary electrons by photon interactions can be calculated.

Figure 3.4 shows the physical arrangement. The metal plate that forms the electrode which carries the high tension (HT) polarizing voltage runs the full length of the chamber, whereas the other plate has the collector electrode as the central part only, separated and electrically isolated from adjacent metal plates called guard rings, which are held at the same electrical potential as the collector electrode. This arrangement ensures that the electric field within the region of the collector electrode is uniform and perpendicular to that electrode. Any ions produced in air within the region ABCD on the diagram will be collected on the collector electrode, whereas any ions produced outside this region will be collected on the guard rings and will not be included in the measurement.

Charged particle equilibrium

The shaded region in Figure 3.4 indicates the volume of air of interest irradiated by the photon beam, being specified by the cross-sectional area of the photon beam and the length of the collector electrode. The mass of air within this volume depends upon atmospheric conditions (temperature and pressure). Correction for different atmospheric conditions is covered in a later section.

Some electrons (such as trajectory 1) emanating from this region will lose all their kinetic energy within region ABCD and will have the ions collected by the collector electrode. Other electrons (such as trajectory 2) emanating from the air volume will pass beyond the boundaries of region ABCD such that some of their ions will be lost to the collector electrode, thereby reducing the measurement of ionization. However, other electrons emanating from outside the air volume may cause ionization within region ABCD that will be collected and measured as indicated by trajectory 3, thereby increasing the measurement of ionization. Charged particle equilibrium is said to exist when the ionization lost from region ABCD is exactly matched by the ionization gained.

Under the conditions of charged particle equilibrium, the total sum of ion pairs generated by the Compton- and photo-electrons ejected from the shaded volume will be equivalent to that determined by measuring the charge collected on the collector electrode.

For charged particle equilibrium to exist, the path in air before the shaded region is reached must be at least equal to the range in air of the Compton- and photo-electrons. Collimation devices must be sited beyond this range, so that photo-electrons ejected from them cannot reach the measurement region. There must similarly be an equivalent path length of air beyond the distal end of the measurement volume before any exit portal is reached. The whole instrument is therefore very large and unwieldy. Furthermore, it is susceptible to interference from externally generated electric fields and stringent measures have to be adopted to minimizse any such influences.

Practical ionization chambers

The Primary Standard instruments described above are complex, sophisticated and sensitive instruments that are unsuitable for routine use within a hospital environment where small, relatively robust, simple instrumentation is needed.

One such instrument is the ionization chamber.

Bragg-Gray cavity theory

The absorbed dose within any medium cannot generally be measured directly and so a surrogate has to be used. Ionization chamber dosimetry is based upon replacing a small volume of the medium by an air cavity within which the ionization of air by the radiation can be measured and from which the dose to the medium can be determined.

When a medium is irradiated uniformly by electrons, then the fluence of electrons (i.e. the energy carried across unit cross-sectional area) will be the same at all points within the medium. If a small air cavity is introduced of size such that it does not perturb the electron fluence (i.e. does not introduce changes to the energy spectrum or numbers of electrons), then the fluence of electrons in the air is the same as in the medium and the cavity is termed a Bragg-Gray cavity. Under these conditions, the energy per unit mass (absorbed dose) imparted to the air (D_a) is given by:

where Ja is the ionization produced per unit mass of air, W is the average energy lost by the electrons per ion pair formed in the air. If the air is now to be replaced by medium, the energy per unit mass imparted to the medium (D_m) would equal the absorbed dose to air multiplied by the electron mass stopping power for the medium divided by that for air (S/ρ)^m_a (averaged over the energy spectrum of the electrons), i.e.:

This is the basic equation governing the use of ionization chambers in the dosimetry of electron beams. For other charged particle beams, the stopping power ratio for those particles must be used.

Where the medium is irradiated by a photon beam, then photon interactions produce secondary electrons which cause ionization within the air cavity. Provided that interactions of photons with air molecules is negligible, such that all electrons crossing the air cavity arise as secondary electrons from within the medium and that the above conditions relating to constancy of electron fluence are met, then the air volume can be regarded as a Bragg-Gray cavity. The above equation then still holds.

In practice, when using ionization chambers, the air volume is enclosed by a wall of material which differs slightly from both air and the medium. The construction of the chamber may introduce perturbations both to the fluence of electrons crossing the air cavity and to the photon beam itself. A wall of infinitesimally small thickness may be considered as having no impact on either, such that the chamber is effectively an air cavity within the medium. As the wall increases in thickness, then an increasing percentage of secondary electrons crossing the air volume will be from the wall rather than the medium until, in the extreme, all electrons crossing the air volume originate from within the wall. In this situation, the electron fluence across the air volume is the same as the fluence within the wall, and the dose to the wall (D_w) is given by:

Assuming the photon field is not perturbed by the presence of the chamber, then the dose deposited by photons in the medium is related to that deposited in the chamber wall:

where (μ/ρ)^m_w is the ratio of mass absorption coefficient for the medium divided by that for the chamber wall.

The conditions for the above to be strictly valid are not met in practice. For measurement of charged particle beams, the fluence of particles may vary with depth and the introduction of the chamber may cause perturbations to this fluence. In measurement of photon beams, the wall of the chamber may be insufficient to stop electrons from outside it reaching the air volume, and the wall of the chamber differs from the medium in its attenuation and scattering of photons. Energy dependent correction factors need to be applied to the above to adjust for these effects.

Dose determination based on calibrated instruments

The above correction factors are not necessary when ionization chambers are used solely as instruments which are calibrated in terms of absorbed dose to water against a suitable primary standard where their effects are taken into account as an intrinsic part of the calibration process. They are required where calibration is in terms of air kerma. Such calibrations are by a series of intercomparisons that are traceable directly to the national standard instruments described above. The absorbed dose is determined using an instrument calibrated in terms of absorbed dose to water (the UK standard for megavoltage photon beams) is given by:

where D is the dose, R is the mean corrected reading and N_D is the absorbed dose calibration factor.

For kV energy photons in the UK, the chamber calibration (N_k) is in terms of air kerma. A factor, [(μ_en/ρ)w_air], the ratio of mass energy absorption coefficients for water and air, needs to be included to calculate the dose to water, and a perturbation factor (k) as described above needs to be applied. The equation becomes:

The nature and magnitude of the correction factor k depends on whether calibration is carried out in air (for low energy x-rays) or in water. Similar expressions may be derived for other modalities of radiation.

Requirements for practical ionization chambers

Radiation dosimeters based upon ionization chambers have two basic components: the detector chamber which produces electrical charge when irradiated and an associated electrometer, which is an electronic amplifier to which the chamber is connected which is designed specifically for the purpose of measuring charge. The response of the dosimeter represents the response of the chamber to radiation together with the accuracy and consistency of the electrometer in measuring the charge.

Practical instrumentation needs to have a well-determined and predictable, slowly varying response to different energies of radiation, and must be consistent over time.

In addition, other dosimeter requirements are necessary depending upon type of radiation and the nature of the measurement being carried out.

Dosimeter chambers used within Standards Laboratories are specially constructed or selected. Materials used in their construction are fully investigated to determine chemical content and each chamber is meticulously assessed in terms of its assembly and response to radiation. Electronic equipment used to measure the electrical charge is equally carefully designed, constructed and calibrated. The prime requirements here are the elimination of sources of inaccuracy in response and the consistency of that response. The overall accuracy of calibration of these instruments depends upon uncertainties in fundamental parameters being measured and to the extent that systematic uncertainties can be avoided. Overall consistency of calibration is between 0.5 and 1%.

Secondary standard instruments are constructed to less stringent standards, but are required to operate over a range of beam energies and to remain consistent in response between recalibrations by the Standards Laboratories (i.e. 3 years). They must be fully transportable so that they can be used to transfer calibrations to other instruments in beams from different treatment machines, or even across different hospital sites. These chambers maintain an accuracy of calibration around 1%. Guidelines covering secondary standards instruments have been published [5].

Field instruments are used in daily measurements within hospitals. Different types of instrument exist, depending upon the nature of those measurements. Thimble chambers, described in detail in the following section, are generally used for calibration of megavoltage photon beams. Chambers based upon the design of the Farmer chamber [10] feature an air cavity of about 0.6 ml, providing a reasonable balance between the response to radiation and smallness of size, are adequate for measurements in relatively uniform radiation beams with an accuracy of 1–2%. Chambers which have much smaller internal dimensions are used to measure variations in dose distributions, which can be very rapid at beam edges. Here, chambers of 0.1 ml or less may be used, with a trade-off between accuracy of response and spatial resolution. Where there is a rapid variation in dose deposited with depth, such as for measurements in the build-up region of photon beams or in the fall-off region of electron beams, parallel plate chambers are used to ensure good depth resolution for the measurements.

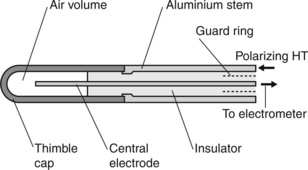
Both thimble ionizations chambers and parallel plate ionization chambers are used widely for routine beam calibration and radiation distribution measurements. Other types of detector systems are useful in particular circumstances and may be used as alternatives to ionization chambers. In particular, in vivo measurements use systems which do not require the application of polarizing voltages, thereby reducing electrical risks to the patient. These various forms of radiation detectors are described within the following sections. Some forms, such as thermoluminescent dosimeters (TLD) have no definitive, maintained calibration and are suitable only for comparative measurements of a radiation dose against a known radiation dose, while other forms (e.g. ionization chambers) do maintain a definitive calibration and can be used as absolute dosimeters.