Radioactivity and Nuclear Transformation
15.0 INTRODUCTION
The nuclei of unstable atoms undergo a transformation during which ionizing radiation (which can be in the form of particles or waves or both) is emitted from the nucleus. This process is referred to as radioactive decay following which the atomic nucleus is in a less unstable (still radioactive) or stable (not radioactive) state. The radioactivity of a material refers to the rate at which it emits radiation. The terms and equations that describe the process of radioactive decay are discussed in this chapter along with the different types of decay processes that are common to radionuclides utilized in nuclear medicine.
15.1 DEFINITIONS
1. Activity
a. The quantity of radioactive material is expressed as the number of radioactive atoms undergoing nuclear transformation per unit time (t).
(i) Activity is equal to the change (dN) in the total number of radioactive atoms (N) in a given time interval (dt), or
(ii) Activity has traditionally been expressed in units of curies (Ci), in honor of Marie Curie, one of the most accomplished women in the history of science. One Ci is defined as 3.70 × 1010 disintegrations per second (dps), approximately the rate of disintegrations from 1 g of radium-226 (Ra-226).
(iii) In honor of Henri Becquerel, the discoverer of radioactivity, the official SI-derived unit of activity was given the special name of becquerel (Bq), which is equal to 1 dps.
(iv) Multiply mCi “millicurie” by 37 to obtain MBq “megabecquerel” or divide MBq by 37 to obtain mCi (e.g., 1 mCi = 37 MBq).
2. Decay constant
a. The decay constant (λ) is equal to the fraction of the number of radioactive atoms remaining in a sample that decay per unit time.
Note that the minus sign indicates that the number of radioactive atoms decaying per unit time (the decay rate or activity of the sample) decreases with time.
b. The relationship between activity A and the decay constant λ can be seen by considering Equation 15-1 and substituting A for -dN/dt in Equation 15-2.
3. Physical half-life
a. The time required for the number of radioactive atoms remaining in a sample to decrease by one half.
(i) From an initial number of radioactive atoms (N0), the number remaining in the sample (N) after (n) half-lives have elapsed is given by Equation 15-4.
TABLE 15-1 PHYSICAL HALF-LIFE (TP½) AND DECAY CONSTANT (λ) FOR RADIONUCLIDES COMMONLY USED IN NUCLEAR MEDICINE
RADIONUCLIDE
TP½
λ
Rubidium-82 (82Rb)
75 s
0.0092 s-1
Fluorine-18 (18F)
110 min
0.0063 min-1
Technetium-99m (99mTc)
6.02 h
0.1151 h-1
Iodine-123 (123I)
13.27 h
0.0522 h-1
Samarium-153 (153Sm)
1.93 d
0.3591 d-1
Yttrium-90 (90Y)
2.69 d
0.2575 d-1
Molybdenum-99 (99Mo)
2.75 d
0.2522 d-1
Indium-111 (111In)
2.81 d
0.2466 d-1
Thallium-201 (201Tl)
3.04 d
0.2281 d-1
Gallium-67 (67Ga)
3.26 d
0.2126 d-1
Xenon-133 (133Xe)
5.24 d
0.1323 d-1
Lutetium-177 (177Lu)
6.7 d
0.1034 d-1
Iodine-131 (131I)
8.02 d
0.0864 d-1
Radium-223 (223Ra)
11.4
0.0608 d-1
Strontium-82 (82Sr)
25.60 d
0.0271 d-1
Cobalt-57 (57Co)
271.79 d
0.0117 d-1
(ii) After 10 half-lives, the number of radioactive atoms in a sample is reduced by approximately a factor of 1,000. After 20 half-lives, it is reduced to about one millionth.
b. The decay constant and the physical half-life are related as follows:
4. Fundamental decay equation
a. The relationship between Nt (the number of radioactive atoms) or At (activity) remaining in a sample at time (t) is given by the following equation:
b. Examples of Tp½ and λ for radionuclides commonly used in nuclear medicine are listed in Table 15-1.
c. A plot of activity as a function of time on a linear scale results in a curvilinear exponential relationship in which the total activity asymptotically approaches zero (Fig. 15-1). If the logarithm of the activity is plotted versus time (semilog plot), this exponential relationship appears as a straight line (Fig. 15-2).
 ▪ FIGURE 15-1 Percentage of initial activity as a function of time (linear scale). |
 ▪ FIGURE 15-2 Percentage of initial activity as a function of time (semilog plot). |
15.2 NUCLEAR TRANSFORMATION
When an unstable (i.e., radioactive) atomic nucleus undergoes the spontaneous transformation, called radioactive decay, radiation is emitted. If the decay product nucleus is stable, this spontaneous transformation ends. If the decay product is also unstable, the process continues until a stable nuclide is reached. Most radionuclides decay in one or more of the following ways: (1) alpha decay (α++), (2) beta-minus emission (β–), (3) beta-plus (positron) emission (β+), (4) electron capture (ε), or (5) isomeric transition via gamma-ray (γ) emission.
1. Alpha decay
a. Alpha particles (i.e., helium nucleus) are emitted from the atomic nucleus of heavy unstable nuclides (A > 150) with discrete energies in the range of 2 to 10 MeV, often followed by γ and characteristic x-ray emissions and sometimes β emissions, Figure 15-3. The photon emissions are often accompanied by the competing processes of internal conversion and Auger electron emission discussed in Chapter 2.
b. Alpha particles are not used in imaging as their ranges are limited to approximately 1 cm/MeV in air and typically less than 100 µm in tissue. Even the most energetic alpha particles cannot penetrate the dead layer of the skin. However, their ability to produce intense ionization tracks make them a potentially serious health hazard should sufficient quantities of alpha-emitting radionuclides enter the body via ingestion, inhalation, or a wound.
c. One alpha-emitting radionuclide radium-223 (Ra-223) is in clinical therapeutic use for the treatment of metastatic prostate cancer while others are being evaluated for therapeutic potential such as astatine-212, bismuth-212, and bismuth-213 (At-211, Bi-212, and Bi-213) chelated to monoclonal antibodies to produce stable radioimmunoconjugates directed against tumors as radioimmunotherapeutic agents.
2. Beta-minus decay
a. Beta-minus decay characteristically occurs with radionuclides that have an excess number of neutrons compared with the number of protons (i.e., a high N/Z ratio).
b. The decay results in the conversion of a neutron into a proton with the simultaneous ejection of a β– particle and an antineutrino (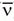
) (Fig. 15-4).
c. Except for their origin (the nucleus), β– particles are identical to and behave as ordinary electrons. However, compared to the β–, the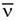
has an infinitesimal mass and is electrically neutral making them very difficult to detect because they rarely interact with matter.
d. Beta decay increases the number of protons by 1 and transforms the atom into a different element with an atomic number Z +1; however, the neutron number is decreased by one thus the mass number remains unchanged. Decay modes in which the mass number remains constant are called isobaric transitions.
e. Radionuclides produced by nuclear fission are “neutron-rich,” and therefore, most decay by β–emission. The β– decay decreases the N/Z ratio, bringing the decay product closer to the line of stability (see Chapter 2).
f. Depending on the radionuclide one or more, β– particles may be emitted during each decay event. While each β– will have a characteristic maximal possible kinetic energy (Emax), that is specific to the radionuclide; almost all are emitted with energies lower than the maximum. The average energy of the β– particles is approximately 1/3 Emax. The balance of the energy is given to the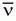
.
g. Any excess energy in the nucleus after beta decay is emitted as γ-rays, internal conversion electrons, and other associated radiations.
▪ FIGURE 15-3 Alpha decay.
▪ FIGURE 15-4 Beta-minus decay.
3. Beta-plus decay (positron emission)
a. Another unstable configuration of the atomic nucleus is when the ratio of the number of neutrons to protons is in a state opposite to that which favors β– decay (i.e., “neutron poor,” low N/Z ratio). In many cases, increase nuclear stability is achieved by the beta-plus (positron) emission decay process.Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
