In nuclear medicine, radiopharmaceuticals given to the patient emit the radiation used to create images or perform therapy. In order to understand how these agents perform and what safety considerations are involved in their use, it is necessary to be familiar with some basic aspects of the physics behind radioactive decay. This chapter discusses radioactive molecules, different types of radioactive decay, and how these emissions interact with matter.
Atomic Structure of Matter
Electronic Structure of the Nucleus
All matter is made up of atoms, which in turn are made up of protons, electrons, and neutrons. Positively charged protons and uncharged neutrons have a similar mass and are known as nucleons because they are located in the nucleus. Although much less massive, electrons orbiting the nucleus possess an opposite negative charge equal in magnitude to that of the protons ( Table 1.1 ) . Some properties of atomic particles are listed, along with important constant values, in Table 1.2 .
| Particle | Charge | Mass (amu or u) a | Mass (MeV) b | Mass (kg) |
|---|---|---|---|---|
| Proton | + 1 | 1.0073 | 938.21 | 1.673 × 10 –27 |
| Neutron | 0 | 1.0087 | 939.51 | 1.675 × 10 –27 |
| Electron | –1 | 0.000549 | 0.511 | 9.11 × 10 –31 |
a One amu = 1.661 × 10 –27 kg or 1/12 atomic mass carbon (1 nucleon from carbon-12 atom).
| Unit of charge | 1 amp·sec |
|---|---|
| Coulomb (C) | 6.24 × 10 18 electrons |
| Electron volt (eV) | 1.602 × 10 –19 J |
| Charge of 1 electron | –1.6 × 10 –19 C |
| Charge of 1 proton | + 1.6 × 10 –19 C |
| Planck’s constant (h) | 6.63 × 10 –34 m 2 ·kg/s |
| Avogadro’s number | 6.02 × 10 23 molecules/g·mole |
| Calorie (cal) | 4.2 Joules |
| Speed of light in a vacuum | 3.0 × 10 8 m/sec |
| Angstrom (Å) | 10 –10 m |
The attraction of the opposite charges keeping the electron in orbit around the nucleus is known as an electrostatic force (or coulombic force; the coulomb is the unit for electric charge). On the other hand, there is also a repulsive, electrostatic force in the nucleus from the like-charged protons pushing apart. The nucleus is held together by the attractive strong nuclear force each nucleon exerts on the other nucleons. Although more powerful than electrical forces, these strong forces act only over extremely short distances. The actual atomic mass is less than the sum of the masses of all its nucleons. This difference in mass, or mass deficit, is manifest in the nuclear binding energy holding the nucleus together (as related by the equation E = mc 2 ).
Elements are organized in the periodic table of the elements (see Appendix 2). All atoms of the same element have the same number of protons. The proton number is also referred to as the atomic number or Z. Thus, all carbon atoms have 6 protons, all oxygen atoms have 8 protons, and all iodine atoms have 53 protons—that is, they have Z numbers of 6, 8, and 53, respectively. Atoms of a particular element can, however, have a varying number of neutrons (referred to as the neutron number, N ). For example, in addition to their 8 protons, some oxygen atoms have 8 neutrons, and others have 7 or 10 neutrons. The total number of nucleons (Z plus N) is known as the atomic mass or atomic number, A. Therefore, in the oxygen example, A would be 15, 16, and 18 for atoms that have 8 protons plus 7, 8, or 10 neutrons, respectively.
Unlike an element, which is characterized only by its number of protons (Z), a nuclide is a nuclear entity characterized by a certain nuclear composition of protons and neutrons as well as a certain energy level. Shorthand notation has been agreed on to describe the makeup of specific nuclides:
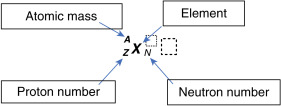
To illustrate this, consider the element iodine, which has 53 protons (Z = 53). If one particular nuclide of the element iodine has 78 neutrons (N = 78), the atomic mass (A) of 53 + 78 equals 131. It can be written as:
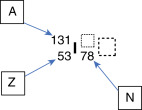
Because the atomic number can be inferred by the element’s symbol, and N = A – Z, this can be shortened:

This can also be written as I-131 or iodine-131. The term isotope describes nuclides of the same element, that is, nuclides with the same number of protons (Z) but potentially differing atomic numbers. Radioisotopes are isotopes that undergo radioactive decay. For example, some common isotopes of iodine are as follows:
I7853131,I7253125,I7153124,I7053123
In medicine, different isotopes have varying properties, such as the types of radiation they emit and how long they remain radioactive, which can determine their usefulness. For example, the beta and high-energy gamma emitter 131 I (I-131) is used for treating thyroid cancer and performing thyroid uptake measurements; 125 I (I-125), a low-energy gamma and x-ray emitter, is used in biological assays and prostate cancer brachytherapy; 124 I (I-124), a positron emitter, can image thyroid cancer with a positron emission tomography (PET) scanner; and 123 I, a moderate-energy gamma emitter, is very commonly used to image benign thyroid diseases and thyroid cancers as well as to calculate thyroid activity (radioactive iodine uptake).
In addition to isotopes, other special terms include isotones, nuclides with the same number of neutrons (e.g., <SPAN role=presentation tabIndex=0 id=MathJax-Element-2-Frame class=MathJax style="POSITION: relative" data-mathml='O814,N713,C612whereN=6′>O814,N713,C612?ℎ???N=6O814,N713,C612whereN=6
O 8 14 , N 7 13 , C 6 12 w h e r e N = 6
); and isobars, those with similar atomic mass numbers (e.g., 14 O, 14 N, 14 C). Nuclides that have the same Z and N numbers (and, therefore, A) but differ in their energy states are called isomers. A well-known example of an isomer in nuclear medicine is technetium-99 (Tc-99) and its metastable state technetium-99m (Tc-99m). Several key terms to know concerning atomic structure are listed in Box 1.1 .
Nucleon—components of the atomic nucleus: protons and neutrons
| Atomic number | Number of protons, or Z |
| Neutron number | Number of neutrons, or N |
| Atomic mass | Sum of the nucleons—protons and neutrons (Z + N)—or atomic number or A |
| Elements | Atoms with the same number of protons ( Z ) |
| Nuclides | Nuclear entity comprised of a particular number of protons (Z) and neutrons (N) as well as energy state of the nucleus |
| Radionuclides | Unstable nuclides: isotopes emitting radiation attempting to reach stability |
| Isotopes | Atoms with the same number of protons: P for proton, P for isoto p e. |
| Isotones | Atoms with the same number of neutrons: N for isoto n e |
| Isobars | Atoms with the same atomic number A: A for isob a r |
| Isomer | Nuclide with same Z and N (so same A) but a different energy level |
Structure of the Orbital Electrons
Our understanding of the atom has evolved, but it is still useful to picture the classic Bohr atom ( Fig. 1.1 ) with electrons arranging themselves into discrete orbital shells ( Table 1.3 ). The innermost shell is referred to as the K shell, and subsequent shells are referred to as L, M, N, O, and beyond. Each shell holds only a set maximum number of electrons, given by 2 n 2 , where n is the shell number). Based on this, for example, the K shell ( n = 1) contains 2 electrons, and the L shell ( n = 2) has 8.
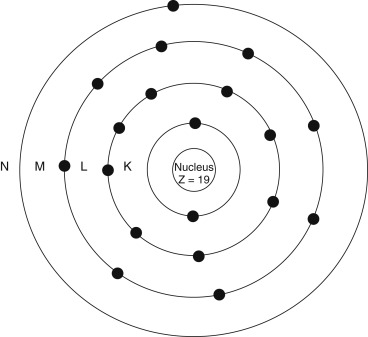
| Term | Comment |
|---|---|
| Electron | Basic elementary particle |
| Orbital electron | Electron in one of the shells or orbits in an atom |
| Valence electron | Electron in the outermost shell of an atom; responsible for chemical characteristics and reactivity |
| Auger electron | Electron ejected from an atomic orbit by energy released during an electron transition |
| Conversion electron | Electron ejected from an atomic orbit because of internal conversion phenomenon as energy is given off by an unstable nucleus |
| Photoelectron | Electron ejected from an atomic orbit as a consequence of an interaction with a photon (photoelectric interaction) and complete absorption of the photon’s energy |
| Compton electron | Electron ejected from orbit after absorbing a portion of a photon’s energy during Compton scatter |
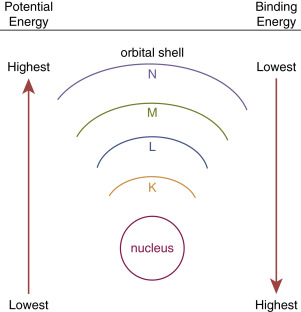
Because electrons are bound by the electrical forces, energy is required to remove an electron from an atom. This orbital binding energy (BE) is characteristic for each particular atom, depending on its Z number, as well as which shell is involved (i.e., it is harder to remove an inner-shell electron than an outer-shell electron; Fig. 1.2 ).
Electromagnetic Radiation
Electromagnetic (EM) radiations, such as visible light, have long been known to have a duality to their nature: behaving in some situations as a wave and in others as a particle, or photon. The EM spectrum ( Fig. 1.3 ) varies in wavelength and frequency, from low-energy radio waves up to high-energy x-rays and gamma (γ) rays as used in medical imaging and therapy.
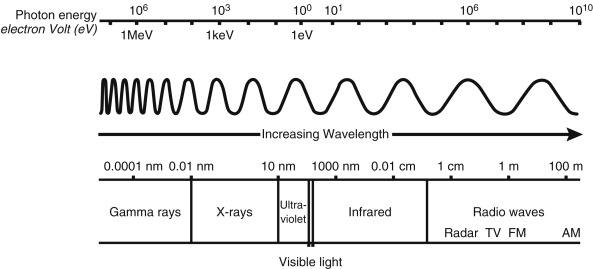
The unit of energy typically used in atomic and nuclear physics is the electron volt (eV), which is the amount of energy an electron garners when crossing an electronic potential difference of 1 volt. One eV is equivalent to 1.6 × 10 –9 joules. EM radiations travel at the speed of light (c) with the known relationship:
c=vλ
The photon energy (E) is related to the frequency of the EM wave by
E=hv

E(keV)=12.4(Å)withtheλmeasuredinangstroms(Å).
Visible light has energy slightly less than 1 eV, whereas x-rays and gamma rays have energies in the range of several thousand eV (or keV) to tens of millions eV (MeV).
X-rays and gamma-ray photons do not differ in their energy levels but in their origin. X-rays are generated from interactions outside the nucleus, whereas gamma rays are generated by transitions within the nucleus. Once created, nothing distinguishes an x-ray from a gamma ray (e.g., A 100-keV x-ray is absolutely identical and indistinguishable from a 100-keV gamma ray).
Production of X-Rays
X-rays are produced in two ways: (1) as a result of the transition of atomic electrons from one orbit to another and (2) from the deacceleration of passing charged particles as they interact with other charged particles, usually as a result of columbic electrical interactions.
Characteristic X-Rays
In the first instance, excited electrons may be removed from their atomic orbit or elevated to a higher-energy orbit. An electron from an outer orbit can drop down to fill the vacancy, and the excess energy, the difference in the binding energy of the shells, can be emitted as an x-ray photon, a fluorescent x-ray ( Fig. 1.4A ). This is also known as a characteristic x-ray because it is specific to not only each element but also to the orbital shell from which it originated. Consider the case of fluorescent or characteristic x-rays from electronic transitions within an iodine atom with the following binding energies: K = 35, L = 5, and M = 1 keV. Thus, the energy of the fluorescent x-rays resulting from the transition of electrons from the L to the K shell (referred to as Kα fluorescent x-rays ) is 30 keV (35 − 5 keV) and that from the transition from the M to the K shell (referred to as K β x-rays ) is 34 keV (35 − 1 keV).
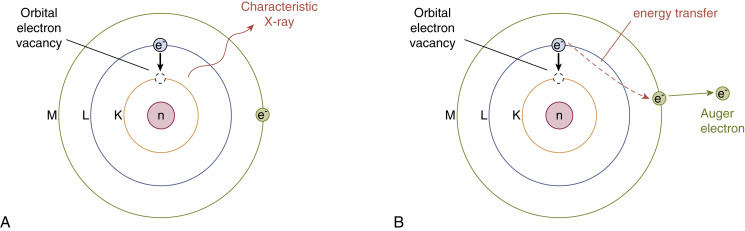
Auger Electrons
There is an alternative outcome to characteristic x-ray emission, where the transition can cause an outer-shell electron to be ejected. This electron is called an Auger (pronounced oh-zhey ) electron (see Fig. 1.4B ). The kinetic energy (KE) of the resultant Auger electron is determined by the binding energy of the orbits involved:
KEAuger=BEInner−BEOuter−BEAuger
Using the example of the iodine atom binding energies again for the transitions shown in Fig. 1.4B , the calculation would then be:
KEAuger=BEKshell−BELshell−BEMshell=35keV−5keV−1keV=29keV
The probability of an Auger electron being emitted is greater in lower Z elements and from outer shells where the binding energy is lower. X-ray fluorescence, on the other hand, is the more likely outcome when binding energy is higher, such as in higher Z elements and from inner-shell electrons.
Particle Deceleration and Bremsstrahlung X-Rays
X-rays can also be produced as a charged particle deaccelerates as it passes an atom. In nuclear medicine, this commonly involves electrons or beta particles passing through soft tissue. In this case, the negatively charged particle is slowed as it interacts with the positively charged nucleus it is passing, causing it to slow. The energy it loses is emitted as radiation referred to as bremsstrahlung (from the German for “braking”) radiation. The magnitude of the bremsstrahlung production increases linearly with the kinetic energy of the incident electron and the Z number of the target material. Thus, bremsstrahlung x-ray production is more likely to occur at higher energies and with high-Z targets. As a result, radiographic systems can generate x-rays by directing an energetic electron beam into a tungsten (Z = 74) target. On the other hand, the intensity of the bremsstrahlung radiation is relatively low when beta particles pass through soft tissue.
Radioactivity and Radioactive Decay
The protons and neutrons can only exist in the nucleus in a limited number of combinations. The remaining unstable atoms may transform to a lower-energy stable state through radioactive decay (or disintegration ), with the excess energy resulting in either particulate emissions or electromagnetic radiation. The initial nuclide, or radionuclide, is known as the parent, and the resultant one after radioactive decay is known as the daughter. Although the daughter nucleus created from a radioactive decay has a lower energy than the parent nucleus, it may not be stable, and thus subsequent radioactive decays may result.
Fig. 1.5 shows a plot of the stable nuclides as a function of the Z number on the x -axis and the N number on the y -axis. At low Z numbers, stable elements tend to have equal numbers of protons and neutrons (e.g., carbon-12, nitrogen-14, and oxygen-16) and lie along or near the Z = N line. However, as the nucleus becomes larger, the repulsive force of the nuclear protons grows, and more neutrons are necessary in the stable nucleus to provide additional attractive nuclear force. Other factors also contribute to the stability and instability of the nucleus. For example, nuclides with even numbers of protons and neutrons tend to be more stable than those with odd Z and N configurations.
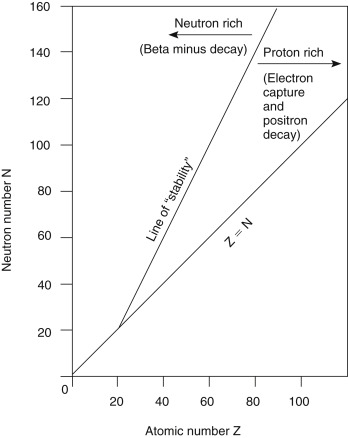
Unstable nuclides fall to either the right or the left of the curve of stability, with those to the right considered proton rich and those to the left neutron rich. As unstable radionuclides decay to entities that are closer to the curve of stability, proton-rich radionuclides tend to decay in a manner that will reduce the Z number and increase the N number, and neutron-rich radionuclides tend to decay in a way that decreases the N number and increases the Z number.
Proton-rich radionuclides can be created by bombarding a certain target material with high-energy protons that can overcome nuclear forces. Typically, a particle accelerator such as a cyclotron is used, increasing kinetic energy by accelerating charged particles to high speeds in a spiral path using alternating high-frequency voltage and electromagnetic fields ( Fig. 1.6 ). Conversely, in artificial production of neutron-rich radionuclides, one typically must use a nuclear reactor to bombard a target with a neutron flux ( Fig. 1.7 ).


Modes of Radioactive Decay
A decay scheme is a way to illustrate the transition from parent to daughter nuclides. In a decay scheme, higher energy levels are toward the top of the figure, and higher Z numbers are to the right of the figure. Transitions that lead to a reduction in energy are represented by an arrow pointing down. If it also results in a daughter nuclide with a change in the Z number, the arrow will point to the left with a decrease in the Z number and to the right if Z is increased.
Alpha Decay
An unstable heavy atom may decay to a nuclide closer to the curve of stability by emitting an alpha particle ( α ) consisting of 2 protons and 2 neutrons (essentially an ionized helium atom):
XZA→YZ−2A−4+α=Yjo9Z−2A−4+He24
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree