As for image registration, the assessment of atlas-based segmentation is still an open question. First, the atlas must represent the subject anatomy as well as possible. Then, the accuracy of the registration algorithm in capturing the anatomical variability between the atlas and the subject is evaluated. It is though not evident to define a quantitative accuracy measure for validation in the particular case of inter-subject non-rigid registration. In [108], Warfield et al. proposed a binary minimum entropy criterion that allows the identification of an intrinsic coordinate system of the subjects under study. Schnabel et al. [89] propose a biomechanical gold standard of non-rigid registration based on finite element methods. Actually, validation of image registration is often application-based and, usually, the evaluation process is only presented as a subsection of the work. However, some comparative studies are published concerning the evaluation of different non-rigid registration techniques. For instance, West et al. [110] present a survey and comparison of multimodal registration techniques. The same is done by Hellier et al. [50] for inter-subject image registration. Recently, Dawant et al. in [30] and Sanchez et al. in [88] proposed a validation study of atlas-based segmentation technique in the framework of subthalamic nuclei localization for the Parkinson surgery.
As mentioned above, a main assumption of the atlas-based segmentation process using registration is that the images to segment are consistent with the atlas. However, possible inconsistencies between two images to be registered can exist. We can distinguished two types of inconsistencies: the intensity-based and the content-based. Trying to find a point to point correspondence between inconsistent images is a challenging task. In the literature several methods have been proposed to remove these inconsistencies. For example, different intensity ranges or the presence of a bias field in the intensity of the target images can be corrected in a pre-processing step by an histogram equalization [91] or a bias correction algorithm [61]. Some similarity measures like gradient-based [15], joint-entropy [20, 94] or mutual information [65, 82, 106] permit the registration of images from different modalities. For content-based inconsistencies, geometrical models have been proposed either to introduce the inconsistent object in the atlas [6, 7, 83] or to force corresponding objects to match [64].
3 Atlas-based Segmentation in Pathological Cases
Atlas-based segmentation has been of limited use in presence of large space-occupying lesions. In fact, brain deformations induced by such lesions may dramatically shift and deform functionally important brain structures. In [7, 83] we presented the problem of inter-subject registration of MR images with large tumors, inducing a significant shift of surrounding anatomical structures. In such pathological cases, the goal of the registration becomes even more complex: it not only tries to capture the normal anatomical variability between subjects but also the deformation induced by the pathology. Moreover, the anatomical meaningful correspondence assumption done in the atlas-based segmentation paradigm is usually strongly violated since voxels located inside the damaged area have no correspondence to the atlas. However, precise segmentation of functionally important brain structures would provide useful information for therapeutic consideration of space-occupying lesions, including surgical, radio-surgical, and radiotherapeutic planning, in order to increase treatment efficiency and minimize neurological damage.
Two early works related to atlas-based segmentation in presence of space-occupying tumors were published in the late 90s. Kyriacou et al. [59] proposed a biomechanical model of the brain using a finite-element method. On the other hand, Dawant et al. [28] relied on a simpler approach based on optical-flow – Thirion’s demons algorithm [98] – for both tumor growth modeling and atlas matching deformation. Their solution was called seeded atlas deformation (SAD), as they put a seed with the same intensity properties as the lesion in the atlas image, and then computed the non-rigid registration. Other methods [36, 92, 93] locally adapted the elasticity of the transformation, rather than modeling the deformation induced by the tumor, in a way that large deformations induced by the tumor can be captured. Recently, Nowinski et al [74] proposed to use a Talairach registration followed by a three-dimensional nonlinear tumor deformation based on a geometric assumption, as in [3, 7], that the tumor compresses its surrounding tissues radially. A more sophisticated model of lesion growth was proposed by Mohamed et al. [71] based on 3D biomechanical finite element model.
Our proposed solution [7, 83] improved the SAD: instead of applying the nonlinear registration algorithm to the whole image, a specific model of tumor growth inside the tumor area was proposed, which assumed the tumor growth radial from a single voxel seed. Demons algorithm [98] was used outside the tumor area and the displacement vector field was regularized by an adaptive Gaussian filter to avoid possible discontinuities. Note that this method does not apply to infiltrating tumors or take into account the presence of the edema.
3.1 Methodology
Our approach is called model of lesion growth (MLG), and it works in 4 steps. First, an affine transformation is applied to the brain atlas in order to globally match the patient’s volume [27]. Second, the lesion is automatically segmented [57, 107]. Thirth, the atlas is manually seeded with a voxel synthetic lesion placed on the estimated origin of the patient’s lesion. At this point, the affine registration ensures that the small displacement assumption is respected in the region of the brain that is far from the tumor. Meanwhile, the segmentation of the tumor volume and the manual selection of the tumor seed provides an adequate model for the tumor and its influence on immediately surrounding tissues. Fourth, the proposed non-rigid deformation method distinguishes between those two areas fixed from the segmentation of the lesion. The instantaneous displacement field is computed as:
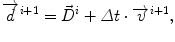
where Δ t=1, 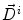 is the current total displacement field. Outside the tumor, the instantaneous force
is the current total displacement field. Outside the tumor, the instantaneous force 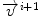 (velocity) for each demon point
(velocity) for each demon point 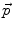 at iteration i+1, is computed as
at iteration i+1, is computed as
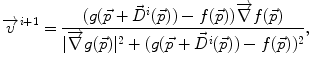
where f(⋅ ) and g(⋅ ) are the image intensities. Thus, there is a displacement in the direction of the gradient provided by both a difference in image intensities and a reference image gradient different from zero. Note that (2) is asymmetrical, that is, it gives different results depending on which image is chosen as the reference and which is chosen to be floating. As proposed by Thirion [98], bijectivity is ensured by computing at each iteration both the direct deformation field (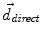 , from Eqs. (1) and (2)) and the inverse deformation field (
, from Eqs. (1) and (2)) and the inverse deformation field (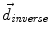 , also from Eqs. (1) and (2) but replacing f instead of g and viceversa). Then, a residual vector field
, also from Eqs. (1) and (2) but replacing f instead of g and viceversa). Then, a residual vector field 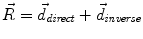 is equally distributed onto the two deformation fields:
is equally distributed onto the two deformation fields:
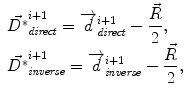
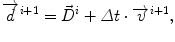
(1)
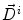 is the current total displacement field. Outside the tumor, the instantaneous force
is the current total displacement field. Outside the tumor, the instantaneous force 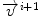 (velocity) for each demon point
(velocity) for each demon point 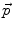 at iteration i+1, is computed as
at iteration i+1, is computed as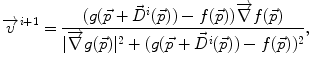
(2)
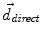 , from Eqs. (1) and (2)) and the inverse deformation field (
, from Eqs. (1) and (2)) and the inverse deformation field (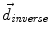 , also from Eqs. (1) and (2) but replacing f instead of g and viceversa). Then, a residual vector field
, also from Eqs. (1) and (2) but replacing f instead of g and viceversa). Then, a residual vector field 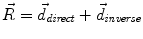 is equally distributed onto the two deformation fields:
is equally distributed onto the two deformation fields: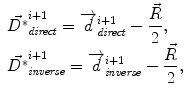
(3)
Inside the tumor, the tumor growth model assumes a radial growth of the tumor from the tumor seed, i.e.
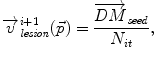
where  is the instantaneous velocity inside the lesion area,
is the instantaneous velocity inside the lesion area, 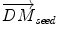 is the distance from the corresponding point
is the distance from the corresponding point 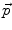 to the seed, and N i t is the number of iterations of the deformation algorithm that have to be performed. Then, the deformation field
to the seed, and N i t is the number of iterations of the deformation algorithm that have to be performed. Then, the deformation field 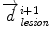 is computed similarly as in (2). The bijectivety inside the lesion area is ensured by forcing
is computed similarly as in (2). The bijectivety inside the lesion area is ensured by forcing 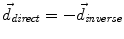 . This model allows the points inside the lesion area to converge towards the seed voxel2, while remaining simple and allowing any number of iterations to take place outside the tumor volume.
. This model allows the points inside the lesion area to converge towards the seed voxel2, while remaining simple and allowing any number of iterations to take place outside the tumor volume.
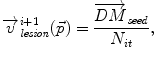
(4)
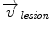 is the instantaneous velocity inside the lesion area,
is the instantaneous velocity inside the lesion area, 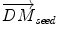 is the distance from the corresponding point
is the distance from the corresponding point 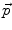 to the seed, and N i t is the number of iterations of the deformation algorithm that have to be performed. Then, the deformation field
to the seed, and N i t is the number of iterations of the deformation algorithm that have to be performed. Then, the deformation field 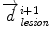 is computed similarly as in (2). The bijectivety inside the lesion area is ensured by forcing
is computed similarly as in (2). The bijectivety inside the lesion area is ensured by forcing 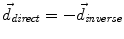 . This model allows the points inside the lesion area to converge towards the seed voxel2, while remaining simple and allowing any number of iterations to take place outside the tumor volume.
. This model allows the points inside the lesion area to converge towards the seed voxel2, while remaining simple and allowing any number of iterations to take place outside the tumor volume.The displacement vector computed at every voxel using either the demons force (1) or the tumor growth model (4) is regularized by an adaptive Gaussian filter to avoid possible discontinuities
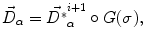
where 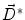 is the deformation field at the current iteration, α refers to direct and inverse, G(σ) is the Gaussian filter with standard deviation σ, and
is the deformation field at the current iteration, α refers to direct and inverse, G(σ) is the Gaussian filter with standard deviation σ, and 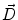 is the regularized deformation field that will be used in Eq. (1) the next iteration. In fact, three different σ areas are considered: inside the lesion area, close to the lesion (within 10 m m of the tumor) where large deformations occur, and the rest of the brain. Smoothing is not necessary inside the lesion because the vector field induced by (4) is highly regular and the continuity is ensured. So, σ = 0 inside the lesion area. In the region close to the tumor (including the tumor contour) there are large deformations due to the tumor growth. Then, it is necessary to allow large elasticity, i.e. σ should have a small value, typically 0. 5 mm. In the rest of the brain, deformations are smaller, due primarily to inter-patient anatomical variability. So, a larger σ proves to be better, as it simulates a more rigid transformation. Previous studies [3] suggest that a typical σ to match two healthy brains is about 0. 5 m m and 1 m m. In what follows, σ = 0. 8 mm is used. The number of iterations is arbitrarily fixed to
is the regularized deformation field that will be used in Eq. (1) the next iteration. In fact, three different σ areas are considered: inside the lesion area, close to the lesion (within 10 m m of the tumor) where large deformations occur, and the rest of the brain. Smoothing is not necessary inside the lesion because the vector field induced by (4) is highly regular and the continuity is ensured. So, σ = 0 inside the lesion area. In the region close to the tumor (including the tumor contour) there are large deformations due to the tumor growth. Then, it is necessary to allow large elasticity, i.e. σ should have a small value, typically 0. 5 mm. In the rest of the brain, deformations are smaller, due primarily to inter-patient anatomical variability. So, a larger σ proves to be better, as it simulates a more rigid transformation. Previous studies [3] suggest that a typical σ to match two healthy brains is about 0. 5 m m and 1 m m. In what follows, σ = 0. 8 mm is used. The number of iterations is arbitrarily fixed to 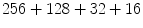 from low to high resolution scale and it stops at the end of the iterations. The algorithm is implemented in a multiscale way: a first match is made with downsampled images and the resulting transformation is upsampled to initialize the next match with finer image resolution.
from low to high resolution scale and it stops at the end of the iterations. The algorithm is implemented in a multiscale way: a first match is made with downsampled images and the resulting transformation is upsampled to initialize the next match with finer image resolution.
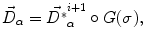
(5)
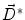 is the deformation field at the current iteration, α refers to direct and inverse, G(σ) is the Gaussian filter with standard deviation σ, and
is the deformation field at the current iteration, α refers to direct and inverse, G(σ) is the Gaussian filter with standard deviation σ, and 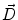 is the regularized deformation field that will be used in Eq. (1) the next iteration. In fact, three different σ areas are considered: inside the lesion area, close to the lesion (within 10 m m of the tumor) where large deformations occur, and the rest of the brain. Smoothing is not necessary inside the lesion because the vector field induced by (4) is highly regular and the continuity is ensured. So, σ = 0 inside the lesion area. In the region close to the tumor (including the tumor contour) there are large deformations due to the tumor growth. Then, it is necessary to allow large elasticity, i.e. σ should have a small value, typically 0. 5 mm. In the rest of the brain, deformations are smaller, due primarily to inter-patient anatomical variability. So, a larger σ proves to be better, as it simulates a more rigid transformation. Previous studies [3] suggest that a typical σ to match two healthy brains is about 0. 5 m m and 1 m m. In what follows, σ = 0. 8 mm is used. The number of iterations is arbitrarily fixed to
is the regularized deformation field that will be used in Eq. (1) the next iteration. In fact, three different σ areas are considered: inside the lesion area, close to the lesion (within 10 m m of the tumor) where large deformations occur, and the rest of the brain. Smoothing is not necessary inside the lesion because the vector field induced by (4) is highly regular and the continuity is ensured. So, σ = 0 inside the lesion area. In the region close to the tumor (including the tumor contour) there are large deformations due to the tumor growth. Then, it is necessary to allow large elasticity, i.e. σ should have a small value, typically 0. 5 mm. In the rest of the brain, deformations are smaller, due primarily to inter-patient anatomical variability. So, a larger σ proves to be better, as it simulates a more rigid transformation. Previous studies [3] suggest that a typical σ to match two healthy brains is about 0. 5 m m and 1 m m. In what follows, σ = 0. 8 mm is used. The number of iterations is arbitrarily fixed to 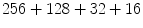 from low to high resolution scale and it stops at the end of the iterations. The algorithm is implemented in a multiscale way: a first match is made with downsampled images and the resulting transformation is upsampled to initialize the next match with finer image resolution.
from low to high resolution scale and it stops at the end of the iterations. The algorithm is implemented in a multiscale way: a first match is made with downsampled images and the resulting transformation is upsampled to initialize the next match with finer image resolution.3.2 Results
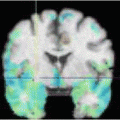
The result after applying these steps is a deformed brain atlas in which a tumor has grown from an initial seed, causing displacement and deformation to the surrounding tissues. After this, structures and substructures from the brain atlas may be projected to the patient’s image. This is illustrated in Fig. 2. The need of a correct estimation of the tumor growth in order to obtain a good final segmentation of the structures directly displaced and deformed by the lesion is proven in [7]. As illustrated in Fig. 3, without an explicit model of tumor growth, SAD cannot grow the small seed until the final tumor size. However, it seems that a good deformation has been obtained in the rest of the brain. Thus, since we are interested in the deep brain structures and not in the tumor itself, the need of simulating the lesion growth could be questionable. Let us then compare the accuracy of the segmentation results of the ventricles, the thalamus and the central nuclei for both approaches. The obtained results, Fig. 4 show that the MLG performs clearly better in the case of the structures near the tumor (thalamus and central nuclei). The most critical structure is the central nuclei (MLG in green and SAD in red) since it is initially placed inside the tumor area. In this case, SAD method fails because the central nuclei segmentation is placed inside the tumor area. On the contrary, MLG pushes the central nuclei out of the tumor region and it obtains a better segmentation.
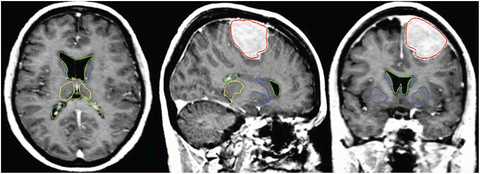
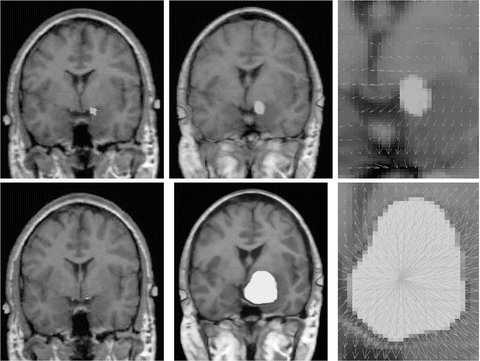
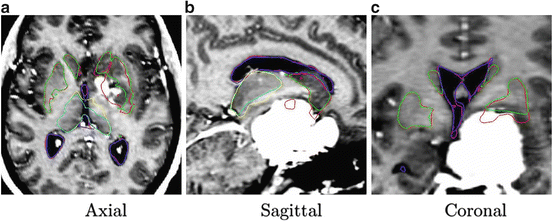

Fig. 2
Segmentation results after applying the MLG algorithm. Displayed structures are: tumor (red), ventricles (green), thalamus (yellow), and central nuclei (blue)

Fig. 3
Top and bottom row, without and with model of lesion growth, respectively. First column, seeded atlas (small seed on top and one voxel seed on bottom). Second column, deformation of seeded atlas. Third column, deformation field in the tumor area

Fig. 4
Importance of the tumor growth model: without (SAD) and with (MLG) model of lesion growth, respectively. Segmented structures: ventricles (MLG in blue and SAD in magenta), thalamus (MLG in cyan and SAD in yellow), and central nuclei (MLG in green and SAD in red)
3.3 Limitations and future work
Our proposed method in [7, 83] increases the robustness of previous existing methods but other limitations arise: the placement of the seed needs expertise and previous segmentation of the lesion is still necessary. Also, since the Demons algorithm [98] uses the sum of the mean squared differences of intensities as similarity measure, the contrast agent (often present in MR scans of such pathologies) induced some errors in the deformation field. Recently, we proposed in [6] a Mutual Information (MI) flow algorithm combined with the same radial growth model presented here. This approach is in fact very similar to the one presented in [7, 83] but MI flow algorithm has proven its robustness to intensity inconsistencies between the atlas and the patient images.
Other limitations persist and they are shared by all voxel-based methods since they often lead to a compromise between the accuracy of the resulting segmentation and the smoothness of the transformation. In our solutions, the regularization of the deformation field is done by an adaptive Gaussian filtering and three different elasticities are allowed according to the distance to the tumor: inside the tumor the radial force ensures the regularity, near the tumor large deformability is allowed and far from the lesion elasticity modeling normal anatomy deformations is applied. A more realistic model of deformability would be to consider not only the distance to the tumor but also the implicit elasticity of some structures such the ventricles, midsagittal plane or skull. This could be included as proposed by Duay et al. [36] by considering that different anatomical structures in the atlas have different elasticity parameters σ but the estimation of these elasticity parameters remains not straightforward. However, even if a better deformability is modeled, voxel-based method still miss local registration constraints that could help selected atlas contours to match their corresponding contours in the patient image.
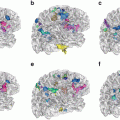
To cope with this problem, more local constraints have to be included in the atlas registration process for instance by incorporating local statistical measures in the registration process as proposed recently by Commowick et al. in [24]. In our opinion, among the different techniques proposed so far for image analysis, the active contour framework is particularly well suited to define and implement local constraints but it was initially designed for image segmentation. Recently, new algorithms including active contour constraints in a registration process have been proposed. These algorithms perform in fact a registration and segmentation tasks jointly (see Sect. 4.1). We proposed in [34, 35, 37, 45] such type of algorithm and we show in Fig. 5 some preliminary results with in a tumor growth application. The atlas and the patient images are respectively shown in Figs. 5(a) and 5(b). These images correspond to 2D slices extracted from 3D brain MR images. A one-voxel seed (shown in Fig. 5(a) by a red point) has been inserted inside the atlas to model the tumor growth. The difference between this model and the tumor growth model presented above is that this seed corresponds to the initial position of an active contour. This active contour is going to segment the tumor of the patient image during the registration process. Thus, with this model, the pre-segmentation of the patient image is not anymore required. Contours of the objects of interest selected in the atlas (the head in green, the brain in yellow, the ventricles in blue and the tumor in red) are superimposed to all images. Our active contour-based algorithm permits to select the atlas contours that will drive its registration. In this case, the registration was performed following the registration of the head contour and the tumor growth only. The rest of the image just follow the deformation interpolated from the displacement of the selected contours. Fig. 5(c) shows the segmentation result obtained after this type of registration and Fig. 5(d) shows the corresponding deformation field. We can see that the registration of the selected green and red contours are bringing the yellow and blue contours closer to their target contours. This object-based registration process points out the spatial dependance that exists between anatomical structures. Such spatial dependance can be exploited in a hierarchical atlas as described in Sect. 4.2.
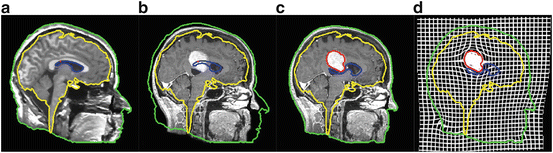

Fig. 5
Active contour-based registration of an atlas on a brain MR image presenting a large occupying tumor. (a) Intensity atlas [58] with objects of interest (the head in green, the brain in yellow, the ventricles in blue, and the tumor one-voxel seed in red). (b) Atlas contours superimposed to the patient image. (c) Results of the joint segmentation and registration driven by the external contour of the head and the tumor contour. (d) Corresponding deformation field
The registration framework we propose allows not only to easily include object-based registration constraints but also to select different type of segmentation forces derived from the active contour framework for the registration of different structures in the atlas. Like the biomechanical methods, this algorithm can also be seen as a surface-based registration method. Its first difference is that it computes the deformation based on the image and not on mechanical or biological laws. This implies that its accuracy does not depend on a good physical modeling of the tissues. Above all, as mentioned above, its main advantage is that it does not need a pre segmentation of the patient image. The contours defined in the atlas evolve following an energy functional specially defined to be minimal when they have reached the desired object contours, as in the active contour-based segmentation framework [76]. Unfortunately, the main limitation of the surface to surface registration algorithm remains. As the deformation is only based on contours of interest, the probability of registration errors increases more we are far from these contours. As far as we know, most of the existing methods for registration of images with space-occupying tumors are either surface-based [59, 62, 71, 116] or voxel-based [7, 13, 28, 36, 83, 93] approaches. However, in our opinion it is worth to study how to combine the advantages of both approaches.
4 Discussion
In this chapter, we saw that the atlas-based segmentation has become a standard paradigm for exploiting spatial prior knowledge in medical image segmentation [16]. The labeled atlas aims to delineate objects of interest in the intensity atlas. The atlas-based segmentation process consists to deform the selected atlas objects in order to better align them with their corresponding objects in the patient image to be segmented. To perform this task, we have distinguished two types of approaches in the literature.
The most known approach reduces the segmentation problem in an image registration problem [5, 10, 14, 18, 22, 29, 43, 53, 86, 98]. Its main advantage is that the deformation field computed from the registration of visible contours allows to easily estimate the position of regions with fuzzy contours or without visible contours, as for instance the subthalamic nuclei (STN) targeting for Parkinson disease [30, 88]. However, these registration algorithms do not exploit the object-based information that could be obtained by combining the intensity and the labeled atlas. This object-based information contains an estimation of the objects position in the patient image, the description of their shape and texture, and the features of their adjacent regions. Therefore, usual atlas-based segmentation methods via registration often miss local constraints to improve the accuracy of the delineation of some objects. Besides, this technique assumes that a point to point correspondence exists between the atlas and the image to be segmented. Then, the presence of inconsistencies can generate registration errors, and consequently segmentation errors, if special schemes are not used (see Sect. 3).
As mentioned in Sect. 2.2, contours in the labeled atlas can be directly deformed without need of a geometrical deformation [8, 19, 115]. The contour morphing technique that has attracted the most attention to date is the active contour segmentation model [56]. Its advantage is that it can exploit the image information directly linked to the object to be delineated. Therefore, active contour models are often able to extract objects where the atlas-based segmentation method by registration fails (see an example on the cerebellum segmentation in [32]). Moreover, this segmentation method allows extracting only the objects that are consistent in the image. Thus, it usually does not need special model to solve the problem of inconsistencies. On the other hand, this segmentation method is very sensitive to the initial position of the atlas contour: the closer to the contours to be detected, the more robust the active contour-based segmentation will be. Besides, this segmentation technique needs prior shape models to be able to estimate the position of regions with fuzzy or without visible contours. Note that these shape models are in fact atlases that are registered with the patient image during the process to incorporate prior knowledge in the active contour segmentation. See [17, 75, 78, 79, 104] for examples of active contour segmentation of medical images with shape priors.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree