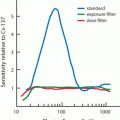
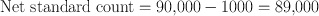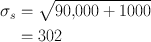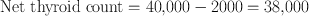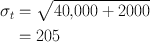The standard deviation of a series of measurements indicates the deviation from the mean value and is a measure of the precision of the measurements . Radioactive decay follows the Poisson distribution law, from which one can show that if a radioactive sample gives an average count of 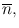 then its standard deviation σ is given by
then its standard deviation σ is given by
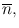 then its standard deviation σ is given by
then its standard deviation σ is given by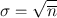
(4.1)
The mean of measurements is then expressed as
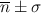
Gaussian Distribution
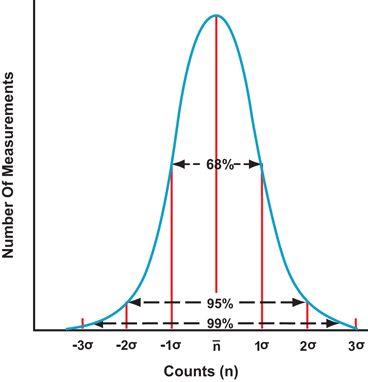
If a series of measurements are made repeatedly on a radioactive sample giving a mean count 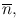 then the distribution of counts would normally follow a Poisson distribution. If the number of measurements is large, the distribution can be approximated by a Gaussian distribution , illustrated in Fig. 4.1. It can be seen that 68 % of all measurements fall within one standard deviation on either side of the mean, that is, within the range
then the distribution of counts would normally follow a Poisson distribution. If the number of measurements is large, the distribution can be approximated by a Gaussian distribution , illustrated in Fig. 4.1. It can be seen that 68 % of all measurements fall within one standard deviation on either side of the mean, that is, within the range 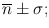 95 % of all measurements fall within the range
95 % of all measurements fall within the range 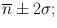 and 99 % fall within the range
and 99 % fall within the range 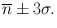 Also the Gaussian curve shows that half of the measurements are below the mean value , and the other half are above it.
Also the Gaussian curve shows that half of the measurements are below the mean value , and the other half are above it.
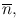 then the distribution of counts would normally follow a Poisson distribution. If the number of measurements is large, the distribution can be approximated by a Gaussian distribution , illustrated in Fig. 4.1. It can be seen that 68 % of all measurements fall within one standard deviation on either side of the mean, that is, within the range
then the distribution of counts would normally follow a Poisson distribution. If the number of measurements is large, the distribution can be approximated by a Gaussian distribution , illustrated in Fig. 4.1. It can be seen that 68 % of all measurements fall within one standard deviation on either side of the mean, that is, within the range 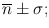 95 % of all measurements fall within the range
95 % of all measurements fall within the range 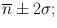 and 99 % fall within the range
and 99 % fall within the range 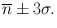 Also the Gaussian curve shows that half of the measurements are below the mean value , and the other half are above it.
Also the Gaussian curve shows that half of the measurements are below the mean value , and the other half are above it.
Fig. 4.1
A Gaussian distribution of radioactive measurements. Note the 68 % confidence level at ± 1σ, 95 % confidence level at ± 2σ, and 99 % confidence level at ± 3σ
The standard deviations in radioactive measurements indicate the statistical fluctuations of radioactive decay. For practical reasons, only single counts are obtained on radioactive samples instead of multiple repeat counts to determine the mean value. In this situation, if a single count n of a radioactive sample is large, then n can be estimated as close to 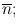 that is,
that is, 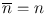 and
and 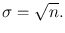 It can then be said that there is a 68 % chance that the true value of the count falls within n ± σ or that the count n falls within one standard deviation of the true value (Fig. 4.1). This is called the 68 % confidence level . That is, one is 68 % confident that the count n is within one standard deviation of the true value. Similarly, 95 % and 99 % confidence levels can be set at two standard deviations (2σ) and three standard deviations (3σ), respectively, of any single radioactive count.
It can then be said that there is a 68 % chance that the true value of the count falls within n ± σ or that the count n falls within one standard deviation of the true value (Fig. 4.1). This is called the 68 % confidence level . That is, one is 68 % confident that the count n is within one standard deviation of the true value. Similarly, 95 % and 99 % confidence levels can be set at two standard deviations (2σ) and three standard deviations (3σ), respectively, of any single radioactive count.
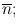 that is,
that is, 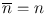 and
and 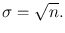 It can then be said that there is a 68 % chance that the true value of the count falls within n ± σ or that the count n falls within one standard deviation of the true value (Fig. 4.1). This is called the 68 % confidence level . That is, one is 68 % confident that the count n is within one standard deviation of the true value. Similarly, 95 % and 99 % confidence levels can be set at two standard deviations (2σ) and three standard deviations (3σ), respectively, of any single radioactive count.
It can then be said that there is a 68 % chance that the true value of the count falls within n ± σ or that the count n falls within one standard deviation of the true value (Fig. 4.1). This is called the 68 % confidence level . That is, one is 68 % confident that the count n is within one standard deviation of the true value. Similarly, 95 % and 99 % confidence levels can be set at two standard deviations (2σ) and three standard deviations (3σ), respectively, of any single radioactive count.Another useful quantity in the statistical analysis of the counting data is the percent standard deviation, which is given as
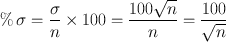
(4.2)
Equation (4.2) indicates that as n increases, the %σ decreases, and hence, precision of the measurement increases. Thus, the precision of a count of a radioactive sample can be increased by accumulating a large number of counts in a single measurement. For example, for a count of 10,000, %σ is 1 %, whereas for 1,000,000, % σ is 0.1 %.
Problem 4.1
How many counts should be collected for a radioactive sample to have a 2 % error at a 95 % comfidence level?
Answer
95 % comfidence level is 2σ, that is, 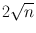
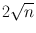
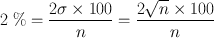
Therefore,
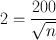
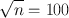
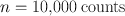
Standard Deviation of Count Rates
The standard deviation of a count rate is
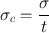
where σ is the standard deviation of the total count n of a radioactive sample obtained in time t. Because n is equal to the count rate c times the counting time t,
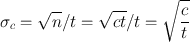
(4.3)
Problem 4.2
A radioactive sample is counted for 12 min and gives 8640 counts. Calculate the count rate and its standard deviation for the sample.
Answer
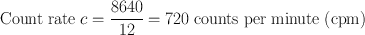
Standard deviation,
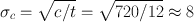
Therefore, the count rate is 720 ± 8 cpm.
Propagation of Errors
Situations arise in which two quantities, say x and y, with their respective standard deviations, σ x and σ y , are either added, subtracted, multiplied, or divided . The standard deviations of the results of these arithmetic operations are given by the following expressions:
Addition:
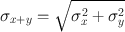
(4.4)
Subtraction:
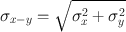
(4.5)
Multiplication:
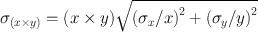
(4.6)
Division:
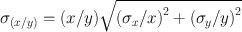
(4.7)
Problem 4.3
A radioactive sample and the background were counted each for 5 min and found to give 8000 counts and 3000 counts, respectively. Calculate the net count rate, its standard deviation, and percent standard deviation.
Answer
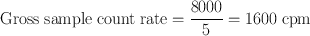
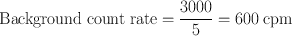
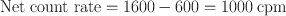
Using Eqs. (4.3) and (4.5)
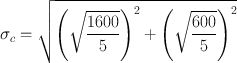
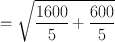
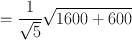
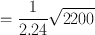
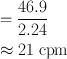
Thus, the count rate of the sample is 1000 ± 21 cpm
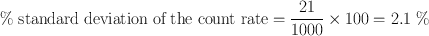
Problem 4.4
A thyroid patient is given a 131I–NaI capsule to measure the 24-h thyroid uptake. The 2-min counts are: standard, 90,000; room background, 1000; thyroid, 40,000; and thigh, 2000. Calculate the thyroid uptake and its percent standard deviation.