Chapter 26 The inverse square law

26.1 Aim

The aim of this chapter is to introduce the reader to the inverse square law and to explore its applications in radiography.

26.2 Intensity of radiation

To understand the inverse square law we must first understand what is meant by the term intensity.

As we have seen in Chapter 17, electromagnetic radiation is composed of quanta, each of which has an energy. If we draw a square of unit area at right angles to the path of a uniform beam of electromagnetic radiation (such as X-rays), then the total per energy second from all the quanta passing through the square is defined as the intensity of the beam, so that:

Definition

The intensity of a beam of electromagnetic radiation at a point is the total energy per second flowing past that point when normalized to a unit area.

It is not necessary at this stage to understand the units of energy or exposure to allow us to apply the inverse square law; these will be dealt with in other chapters.

26.3 Statement of the inverse square law

The intensity of the radiation emitted from a small isotropic source is inversely proportional to the square of the distance from the source, provided there is negligible absorption or scattering of the radiation by the medium through which it passes.

Note: This statement of the inverse square law also gives the conditions under which the law may be directly applied:

• Small source – in practice this means small compared to the distance from the source to the point of measurement.

• Isotropic source – this means that it emits radiation in all directions. This is necessary in order that the intensity of the radiation is independent of the direction from the source.

• No absorption or scattering of radiation – this ensures that the radiation passing through an area is not affected by the medium through which the radiation passes. It is important to remember that back scattering of the beam from objects beyond the point of measurement must also be eliminated, as this would produce an increase in the intensity.

As we will see, it is not possible to meet all of these conditions in many situations in radiography. In such cases, the law must be applied with caution or even with appropriate correction factors (e.g. absorption due to air may be important when we consider low-energy beams of X-rays).

Insight

A situation where the inverse square law does not apply is in the case of a laser beam. Because the light is essentially parallel, the intensity is constant and does not depend on distance from the source.

26.4 Similar-triangles proof of the inverse square law

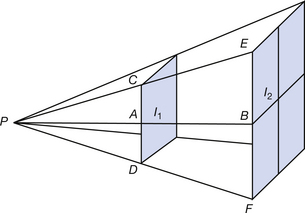
Consider the situation shown in Figure 26.1. The radiation is produced at a point P and is allowed to fall on the square of side CD and the square of side EF. PB is twice the length of PA. Because the triangles are similar, we can say that EF must be twice the length of CD. So the area of the square of side EF is four times the area of the square of side CD.