, predominantly in transmural direction, resulted in a 91 % increase of LV and 20 % increase of RV stroke work. These findings indicate the importance for a more thorough effort to address a realistic myofiber orientation. The currently used model for adaptive myofiber reorientation seems a useful approach to prescribe the myofiber orientations in BiV FE models.
1 Introduction
Biventricular (BiV) finite element (FE) models eventually could be used to assist in clinical decision making in cardiac disease [1–6]. The strength of these models is their ability to describe the relation between local tissue function and global pump function. Therefore, the heart’s geometry, myofiber orientation, and myocardial tissue properties are taken into account. Whenever possible, the model input is based on in vivo measurements. For example, geometrical properties are taken from imaging data and included into models using meshing algorithms [7]. However, usually data from in vitro measurements is used to prescribe local myofiber orientation [8, 9] and myocardial tissue properties. While the morphed myofiber orientation data is fixed, material properties are tuned for maximum agreement between model predicted and clinically measured cardiac function [1, 4].
The accuracy of MRDTI is on the order of  10
10 [10], even in the in vitro case [11, 12], making it hard to assess the true variation of fiber orientation in between hearts. In addition, in models of only the left ventricle (LV) it has been shown that variations in the spatial distribution of myofiber orientations of 8
[10], even in the in vitro case [11, 12], making it hard to assess the true variation of fiber orientation in between hearts. In addition, in models of only the left ventricle (LV) it has been shown that variations in the spatial distribution of myofiber orientations of 8 , introduced variations in myofiber stress of 10 % [13]. In addition, shear deformation could only be realistically predicted when a transmural component in myofiber orientation of
, introduced variations in myofiber stress of 10 % [13]. In addition, shear deformation could only be realistically predicted when a transmural component in myofiber orientation of 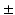 10
10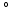 was included [14]. As an alternative approach for estimating myofiber orientation, it has been hypothesized that myofiber orientation is the result of an adaptation process. This hypothesis was successfully tested in an LV model that described the adaptive change of myofiber orientation in response to fiber cross-fiber shear [15, 16]. It remains unclear to what extent the assumption of a generic myofiber orientation influences predictions on cardiac function from BiV FE models and whether adaptive myofiber reorientation could also serve as a method for predicting the myofiber orientation in these models.
was included [14]. As an alternative approach for estimating myofiber orientation, it has been hypothesized that myofiber orientation is the result of an adaptation process. This hypothesis was successfully tested in an LV model that described the adaptive change of myofiber orientation in response to fiber cross-fiber shear [15, 16]. It remains unclear to what extent the assumption of a generic myofiber orientation influences predictions on cardiac function from BiV FE models and whether adaptive myofiber reorientation could also serve as a method for predicting the myofiber orientation in these models.
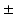 10
10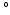 [10], even in the in vitro case [11, 12], making it hard to assess the true variation of fiber orientation in between hearts. In addition, in models of only the left ventricle (LV) it has been shown that variations in the spatial distribution of myofiber orientations of 8
[10], even in the in vitro case [11, 12], making it hard to assess the true variation of fiber orientation in between hearts. In addition, in models of only the left ventricle (LV) it has been shown that variations in the spatial distribution of myofiber orientations of 8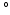 , introduced variations in myofiber stress of 10 % [13]. In addition, shear deformation could only be realistically predicted when a transmural component in myofiber orientation of
, introduced variations in myofiber stress of 10 % [13]. In addition, shear deformation could only be realistically predicted when a transmural component in myofiber orientation of 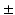 10
10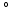 was included [14]. As an alternative approach for estimating myofiber orientation, it has been hypothesized that myofiber orientation is the result of an adaptation process. This hypothesis was successfully tested in an LV model that described the adaptive change of myofiber orientation in response to fiber cross-fiber shear [15, 16]. It remains unclear to what extent the assumption of a generic myofiber orientation influences predictions on cardiac function from BiV FE models and whether adaptive myofiber reorientation could also serve as a method for predicting the myofiber orientation in these models.
was included [14]. As an alternative approach for estimating myofiber orientation, it has been hypothesized that myofiber orientation is the result of an adaptation process. This hypothesis was successfully tested in an LV model that described the adaptive change of myofiber orientation in response to fiber cross-fiber shear [15, 16]. It remains unclear to what extent the assumption of a generic myofiber orientation influences predictions on cardiac function from BiV FE models and whether adaptive myofiber reorientation could also serve as a method for predicting the myofiber orientation in these models.The aim of this study was to investigate to what extent variations in myofiber orientation induced by adaptive reorientation of myofibers according to the model in [15] cause variations in cardiac function in a BiV FE model of cardiac mechanics and whether the adaptation model could be used to refine the myofiber orientation in these models.
2 Methods
Geometry. In the unloaded state, the BiV mesh was described by two intersecting, truncated ellipsoids (Fig. 1A). The 8 parameters listed and explained in Table 1 defined the whole geometry. Values were set such that the LV and RV inner radii were 20 mm and 53 mm, LV and RV inner length were 74 mm and 70 mm, and LV and RV wall volumes were 160 ml and 40 ml, respectively, and both LV and RV cavity volume were 60 ml.
Material Properties. Myocardial tissue Cauchy stress 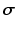 was composed of a passive component
was composed of a passive component 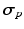 and an active component
and an active component 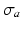 . Passive material behavior was assumed nonlinearly elastic, transversely isotropic, and nearly incompressible. It was described by a strain energy density function that consisted of an isotropic, an anisotropic, and a volume part as described in [17]. Active stress
. Passive material behavior was assumed nonlinearly elastic, transversely isotropic, and nearly incompressible. It was described by a strain energy density function that consisted of an isotropic, an anisotropic, and a volume part as described in [17]. Active stress 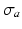 acted in the myofiber direction only. The magnitude of
acted in the myofiber direction only. The magnitude of 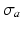 depended on time elapsed since activation
depended on time elapsed since activation 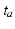 , sarcomere length
, sarcomere length 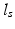 , and sarcomere shortening velocity as described in [14]. Active stress was initiated simultaneously throughout both ventricles with a cycle time of 800 ms.
, and sarcomere shortening velocity as described in [14]. Active stress was initiated simultaneously throughout both ventricles with a cycle time of 800 ms.
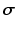 was composed of a passive component
was composed of a passive component 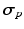 and an active component
and an active component 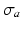 . Passive material behavior was assumed nonlinearly elastic, transversely isotropic, and nearly incompressible. It was described by a strain energy density function that consisted of an isotropic, an anisotropic, and a volume part as described in [17]. Active stress
. Passive material behavior was assumed nonlinearly elastic, transversely isotropic, and nearly incompressible. It was described by a strain energy density function that consisted of an isotropic, an anisotropic, and a volume part as described in [17]. Active stress 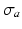 acted in the myofiber direction only. The magnitude of
acted in the myofiber direction only. The magnitude of 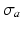 depended on time elapsed since activation
depended on time elapsed since activation 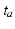 , sarcomere length
, sarcomere length 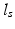 , and sarcomere shortening velocity as described in [14]. Active stress was initiated simultaneously throughout both ventricles with a cycle time of 800 ms.
, and sarcomere shortening velocity as described in [14]. Active stress was initiated simultaneously throughout both ventricles with a cycle time of 800 ms.Adaptive Myofiber Reorientation. Myofiber orientation in the unloaded state 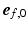 was defined in a local cardiac coordinate system
was defined in a local cardiac coordinate system 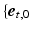 ,
, 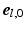 ,
, 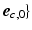 (Fig. 1C). The transmural direction
(Fig. 1C). The transmural direction 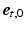 was defined perpendicular to the endo- and epicardial surfaces, the longitudinal direction
was defined perpendicular to the endo- and epicardial surfaces, the longitudinal direction 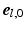 was defined parallel to these surfaces from apex to base, and the circumferential direction
was defined parallel to these surfaces from apex to base, and the circumferential direction 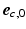 was defined in clockwise direction when viewing the geometry in apex-to-base direction.
was defined in clockwise direction when viewing the geometry in apex-to-base direction. 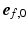 was quantified by two angles. The helix angle
was quantified by two angles. The helix angle 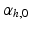 was defined as the angle between
was defined as the angle between 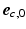 and the projection of
and the projection of 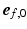 on the circumferential-longitudinal plane (
on the circumferential-longitudinal plane (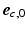 ,
, 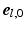 ). The transverse angle
). The transverse angle 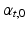 was defined as the angle between
was defined as the angle between 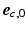 and the projection of
and the projection of 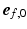 on the circumferential-transmural plane (
on the circumferential-transmural plane (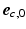 ,
, 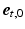 ). To ensure a smooth transition of the coordinate system and myofiber orientation in all regions, including the RV-LV attachment, the bi-directional spherical linear interpolation method of Bayer et al. [18] was used.
). To ensure a smooth transition of the coordinate system and myofiber orientation in all regions, including the RV-LV attachment, the bi-directional spherical linear interpolation method of Bayer et al. [18] was used.
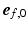 was defined in a local cardiac coordinate system
was defined in a local cardiac coordinate system 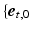 ,
, 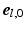 ,
, 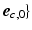 (Fig. 1C). The transmural direction
(Fig. 1C). The transmural direction 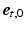 was defined perpendicular to the endo- and epicardial surfaces, the longitudinal direction
was defined perpendicular to the endo- and epicardial surfaces, the longitudinal direction 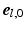 was defined parallel to these surfaces from apex to base, and the circumferential direction
was defined parallel to these surfaces from apex to base, and the circumferential direction 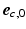 was defined in clockwise direction when viewing the geometry in apex-to-base direction.
was defined in clockwise direction when viewing the geometry in apex-to-base direction. 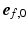 was quantified by two angles. The helix angle
was quantified by two angles. The helix angle 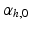 was defined as the angle between
was defined as the angle between 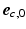 and the projection of
and the projection of 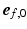 on the circumferential-longitudinal plane (
on the circumferential-longitudinal plane (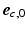 ,
, 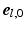 ). The transverse angle
). The transverse angle 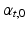 was defined as the angle between
was defined as the angle between 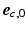 and the projection of
and the projection of 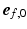 on the circumferential-transmural plane (
on the circumferential-transmural plane (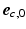 ,
, 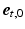 ). To ensure a smooth transition of the coordinate system and myofiber orientation in all regions, including the RV-LV attachment, the bi-directional spherical linear interpolation method of Bayer et al. [18] was used.
). To ensure a smooth transition of the coordinate system and myofiber orientation in all regions, including the RV-LV attachment, the bi-directional spherical linear interpolation method of Bayer et al. [18] was used.During simulation of the cardiac cycle, 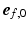 was subject to adaptation that caused a structural change in myofiber orientation in the unloaded reference state. Adaptation of
was subject to adaptation that caused a structural change in myofiber orientation in the unloaded reference state. Adaptation of 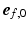 was simulated with the model published by Kroon et al. [15] and explained in detail in [16]. The mechanism behind the incremental update of
was simulated with the model published by Kroon et al. [15] and explained in detail in [16]. The mechanism behind the incremental update of 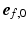 is explained in Fig. 1B and described by the following equation:
is explained in Fig. 1B and described by the following equation:
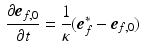
with an adaptation time constant 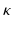 (set to 3200 ms).
(set to 3200 ms). 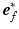 represents the actual myofiber orientation in the deformed tissue corrected for rigid body rotation.
represents the actual myofiber orientation in the deformed tissue corrected for rigid body rotation.
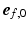 was subject to adaptation that caused a structural change in myofiber orientation in the unloaded reference state. Adaptation of
was subject to adaptation that caused a structural change in myofiber orientation in the unloaded reference state. Adaptation of 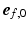 was simulated with the model published by Kroon et al. [15] and explained in detail in [16]. The mechanism behind the incremental update of
was simulated with the model published by Kroon et al. [15] and explained in detail in [16]. The mechanism behind the incremental update of 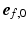 is explained in Fig. 1B and described by the following equation:
is explained in Fig. 1B and described by the following equation: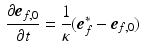
(1)
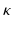 (set to 3200 ms).
(set to 3200 ms). 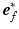 represents the actual myofiber orientation in the deformed tissue corrected for rigid body rotation.
represents the actual myofiber orientation in the deformed tissue corrected for rigid body rotation.Governing Equations and Boundary Conditions. In the model, the quasi-static equations of conservation of linear momentum were solved numerically with a Galerkin type finite element method using 27-noded hexahedral elements with a tri-quadratic interpolation of the displacement field. Rotational movement of LV endocardial base and longitudinal displacement of both LV and RV base were suppressed. LV and RV endocardial surfaces were subjected to a left and right ventricular pressure, 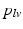 and
and 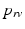 , respectively, computed from the interaction of the LV and RV with a lumped parameter model of both systemic and pulmonary circulation, respectively (Fig. 1A). To capture characteristic of the human circulation, parameter values for resistances and compliances were based on [19, 20].
, respectively, computed from the interaction of the LV and RV with a lumped parameter model of both systemic and pulmonary circulation, respectively (Fig. 1A). To capture characteristic of the human circulation, parameter values for resistances and compliances were based on [19, 20].
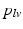 and
and 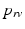 , respectively, computed from the interaction of the LV and RV with a lumped parameter model of both systemic and pulmonary circulation, respectively (Fig. 1A). To capture characteristic of the human circulation, parameter values for resistances and compliances were based on [19, 20].
, respectively, computed from the interaction of the LV and RV with a lumped parameter model of both systemic and pulmonary circulation, respectively (Fig. 1A). To capture characteristic of the human circulation, parameter values for resistances and compliances were based on [19, 20].Simulations Performed. The simulation started with an initial distribution of 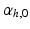 that varied throughout the whole myocardium nonlinearly with the transmural position from 65
that varied throughout the whole myocardium nonlinearly with the transmural position from 65 at the endocardium to -50
at the endocardium to -50 at the epicardium [14]. The initial distribution of
at the epicardium [14]. The initial distribution of 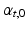 was set to zero.
was set to zero.
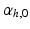 that varied throughout the whole myocardium nonlinearly with the transmural position from 65
that varied throughout the whole myocardium nonlinearly with the transmural position from 65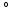 at the endocardium to -50
at the endocardium to -50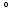 at the epicardium [14]. The initial distribution of
at the epicardium [14]. The initial distribution of 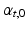 was set to zero.
was set to zero.First, the model ran for 8 consecutive cardiac cycles to approximate a hemodynamic steady state while myofiber reorientation was disabled. In the following cardiac cycles myofiber orientation was adapted per node according to the adaptation model in [15].
Global function was quantified as cardiac output (CO), LV and RV ejection fraction (EF), and stroke work W, which was calculated from the area within the pressure-volume loops for both ventricles. The change in myofiber orientation between the initial and adapted state was quantified by the angle 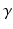 (Fig. 3). This orientation change was further quantified in terms of
(Fig. 3). This orientation change was further quantified in terms of 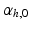 and
and 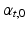 .
.
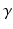 (Fig. 3). This orientation change was further quantified in terms of
(Fig. 3). This orientation change was further quantified in terms of 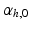 and
and 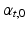 .
.Table 1.
Biventricular geometry input parameter values and explanation.
Parameter | Definition | Value | Unit | Explanation |
|---|---|---|---|---|
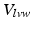 | 160 | [ml] | LV wall volume | |
 Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|