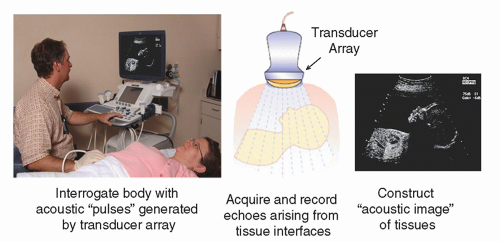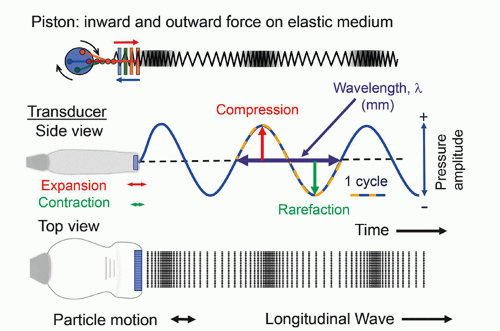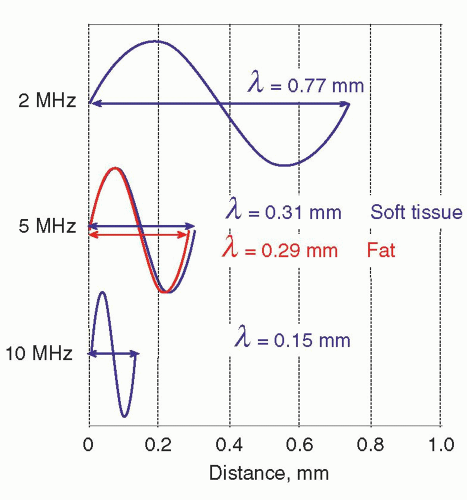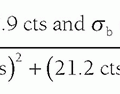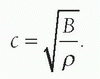
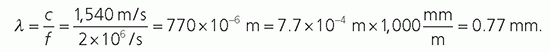
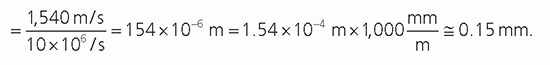
TABLE 14-1 DENSITY, SPEED OF SOUND, AND ACOUSTIC IMPEDANCE FOR TISSUES AND MATERIALS RELEVANT TO MEDICAL ULTRASOUND | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
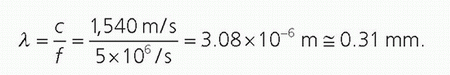
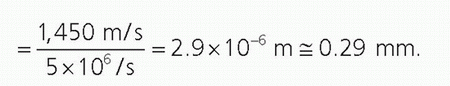
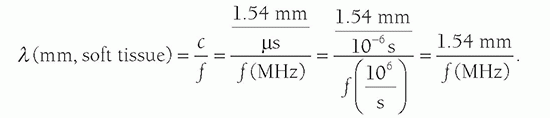
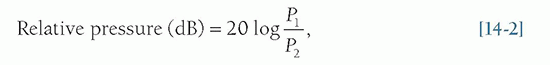
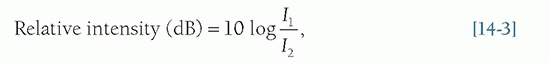
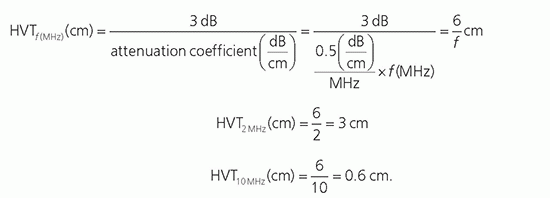
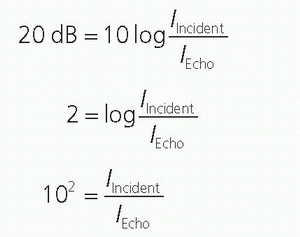
manageable number range. Pressure is proportional to voltage, and Equation 14-2 is important when comparing voltages that are induced by the reception of echoes by the transducer elements (see Section 14.4). Note: when considering pressure or voltage comparisons, the dB scale is a factor of 2 higher compared to intensity comparisons, so the dB scale must be used in context. Using Equation 14-3, an intensity ratio of 106 (e.g., an incident intensity one million times greater than the returning echo intensity) is equal to 60 dB, whereas an intensity ratio of 102 is equal to 20 dB. A change of 10 in the relative intensity dB scale corresponds to an order of magnitude (10 times) change; a change of 20 corresponds to two orders of magnitude (100 times) change, and so forth. When the intensity ratio is greater than one (e.g., the incident ultrasound intensity greater than the detected echo intensity), the dB values are positive; when less than one, the dB values are negative. A loss of 3 dB (-3 dB) represents a 50% loss of signal intensity. The tissue thickness that reduces the ultrasound intensity by 3 dB is considered the “half-value” thickness (HVT). In Table 14-2, intensity ratios, logarithms, and the corresponding intensity dB values are listed.
TABLE 14-2 INTENSITY RATIO AND CORRESPONDING DECIBEL VALUES | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
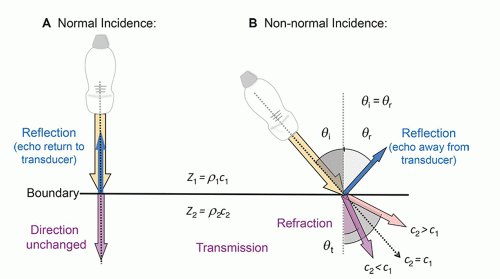
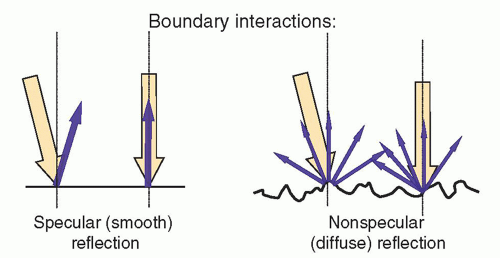
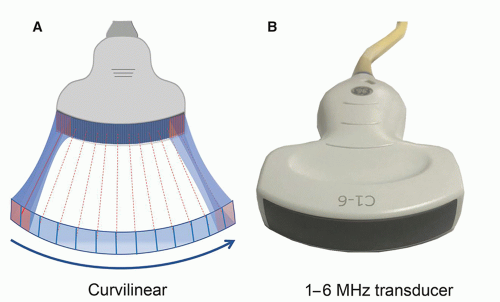
in Table 14-1, right column. The efficiency of sound energy transfer from one tissue to another is largely based upon the differences in acoustic impedance—if impedances are similar, a large fraction of the incident intensity at the boundary interface will be transmitted, and if the impedances are largely different, a large fraction will be reflected. In most soft tissues, these differences are typically small, allowing for ultrasound travel to large depths in the patient.

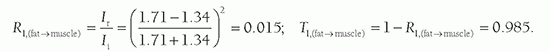
TABLE 14-3 PRESSURE AND REFLECTION COEFFICIENTS FOR VARIOUS INTERFACES | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||
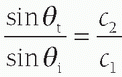 . For small angles, this can be approximated as
. For small angles, this can be approximated as 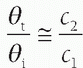 . Figure 14-4B illustrates the refraction angle when the speeds of sound in tissue 1 are greater than or less than tissue 2.
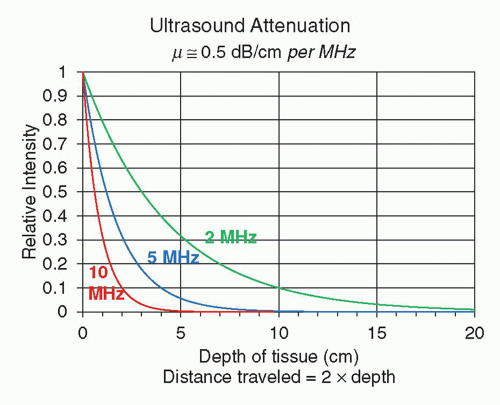
. Figure 14-4B illustrates the refraction angle when the speeds of sound in tissue 1 are greater than or less than tissue 2.logarithmically to the base 10, the beam intensity is attenuated to the power of 10 with distance (See Fig. 14-6). Careful selection of the transducer frequency must be made in the context of the imaging depth needed for an exam. The loss of ultrasound intensity in decibels (dB) can be determined empirically for different tissues by measuring intensity as a function of distance traveled in centimeters (cm) and is the attenuation coefficient µ, expressed in dB/cm. For a given ultrasound frequency, tissues and fluids have widely varying attenuation coefficients chiefly resulting from structural and density differences, as indicated in Table 14-4 for a 1-MHz ultrasound beam.
TABLE 14-4 ATTENUATION COEFFICIENT µ(dB/cm-MHz) FOR TISSUES ENCOUNTERED IN ULTRASOUND | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||
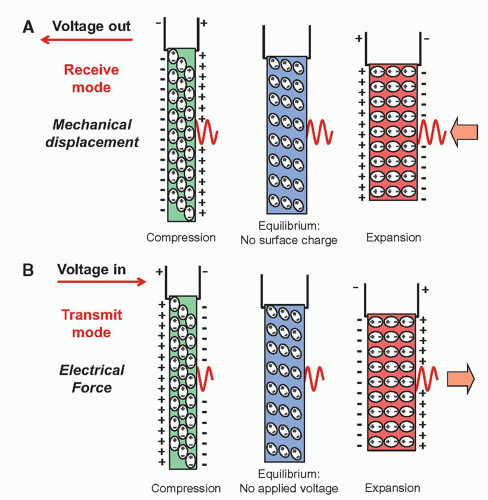
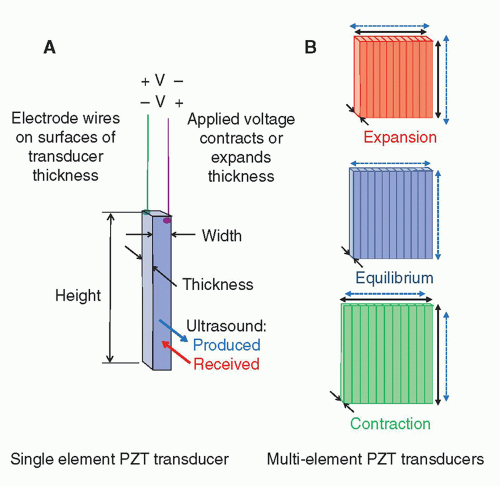
of mechanical strain in response to an applied electrical field. Ultrasound transducers for medical imaging applications employ a synthetic piezoelectric ceramic, lead-zirconate-titanate (PZT), or a silicon-based capacitive micromachined ultrasound transducer (CMUT).
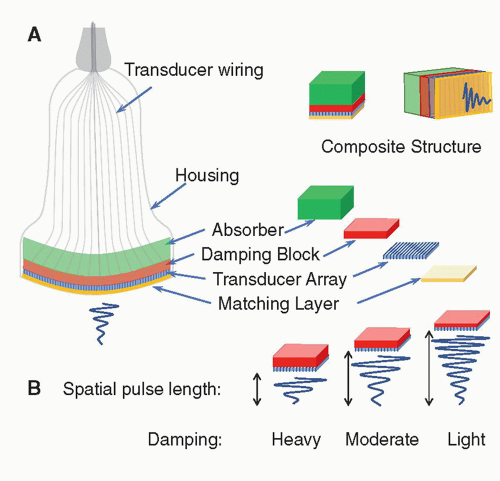
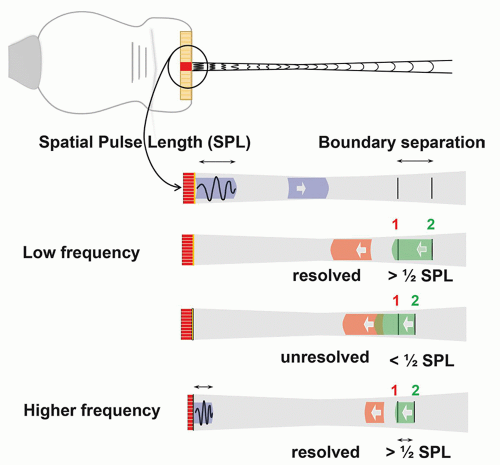
functions in an excitation mode to transmit ultrasound energy, and in a reception mode to receive ultrasound energy. To be able to use the pulse-echo format, there is a need to shorten the pulse.
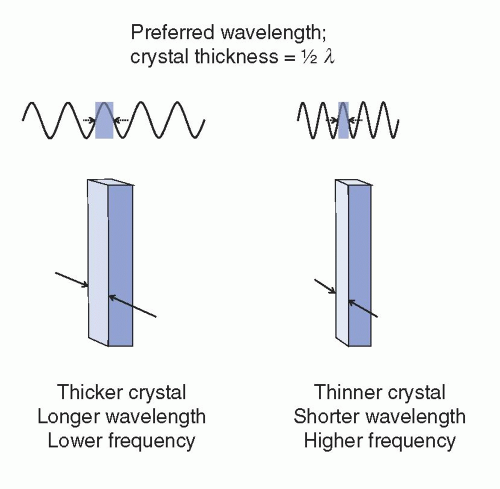
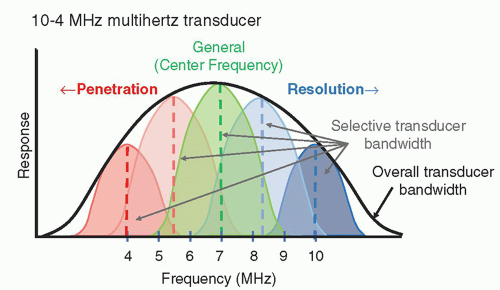
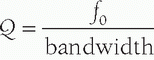 , where f0 is the center frequency and the bandwidth is the width of the frequency distribution. A high “Q” transducer operation has a narrow bandwidth and a long spatial pulse width, which is good for evaluating frequency shifts such as are used in pulsed Doppler studies for measuring blood velocities (Section 14.8). A low “Q” transducer has heavy damping and a rapid ring-down of the crystal vibration to achieve a short SPL for imaging studies.
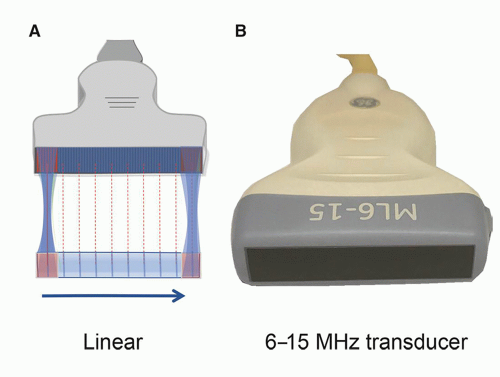
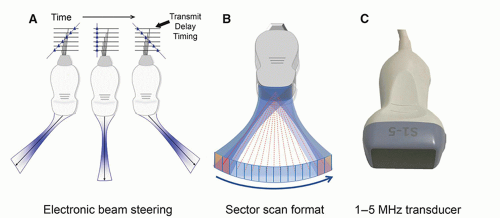
, where f0 is the center frequency and the bandwidth is the width of the frequency distribution. A high “Q” transducer operation has a narrow bandwidth and a long spatial pulse width, which is good for evaluating frequency shifts such as are used in pulsed Doppler studies for measuring blood velocities (Section 14.8). A low “Q” transducer has heavy damping and a rapid ring-down of the crystal vibration to achieve a short SPL for imaging studies.can be interactively selected by the operator. The smaller physical dimension of the transducer array is useful for access to intercostal acoustic windows when performing heart and thoracic imaging exams. With a sector-scan format, the FOV dimension can be limited in regions proximal to the transducer array. A 1-5 MHz phased array transducer is shown in Figure 14-14C.
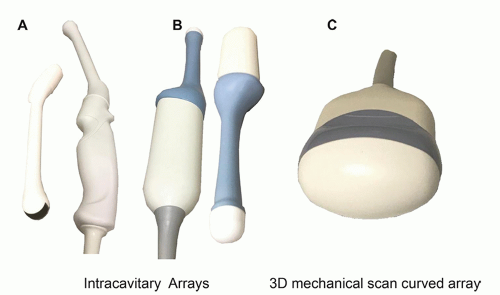
intraoral applications. The mechanically scanned curved array transducer is commonly used in obstetrical evaluations for 3D volume image acquisitions. Mechanical scanning of the curved array occurs simultaneously with 2D image acquisition and is synchronized to provide volumetric sampling over a ˜90° by ˜90° FOV range as a function of time. Shaded surface and volumetric rendering generate real-time 3D movies of the fetus, as discussed in Section 14.6.
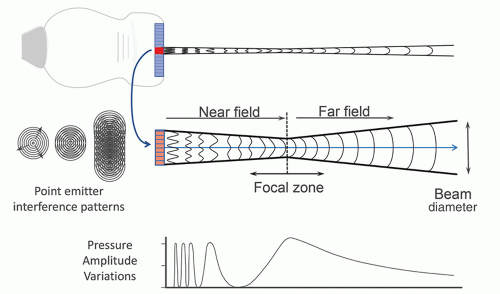
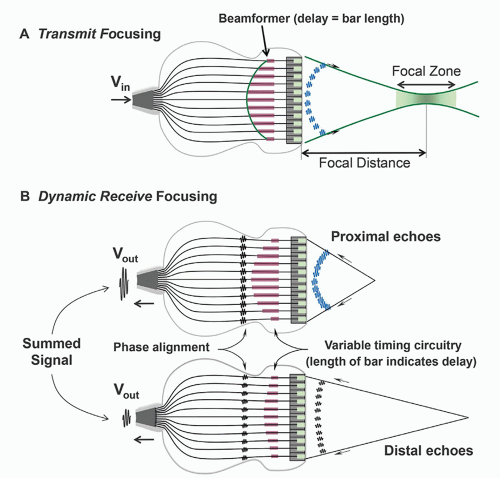
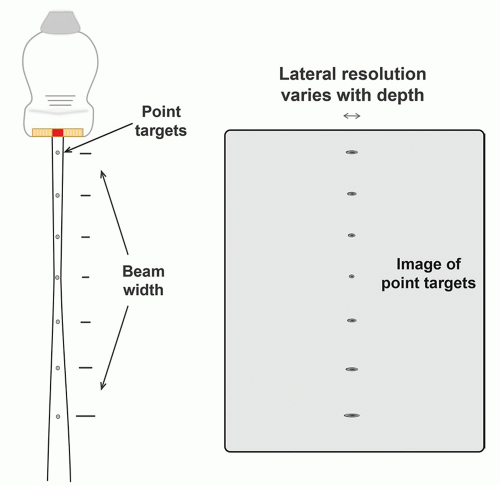
largely confined to the dimensions of the active portion of the transducer surface, with the beam converging to approximately half the transducer area at the end of the near field. The near field length is dependent on the transducer area and inversely proportional to propagation wavelength, so higher transducer frequency results in an extended near field. Lateral resolution (the ability of the system to resolve objects in a direction perpendicular to the beam direction) depends on the lateral beam dimension and is best at the end of the near field for an unfocused transducer element aperture (e.g., a subgroup of linear array transducer elements fired simultaneously).
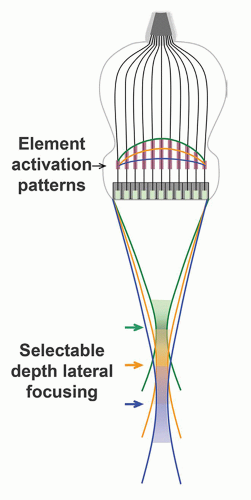
collimated beam that has properties like the properties of a single crystal area transducer of the same size. Thus, for a subgroup of simultaneously fired transducers in a linear array, the focal distance is a function of the transducer area (height/width) and the transducer frequency. With slight differences in excitation time for individual elements in the subgroup aperture (or full phased array), wave interactions and summations can focus the beam.
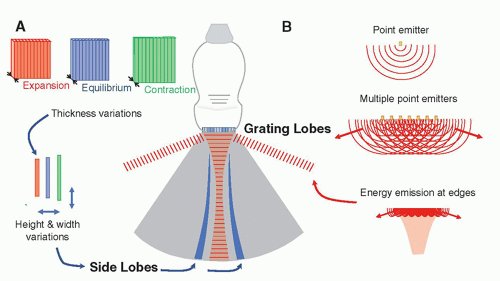
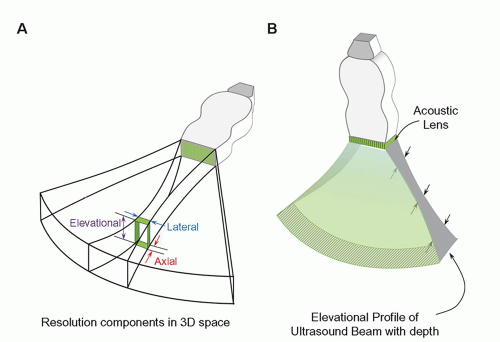
resolvability for array transducers. The use of an acoustic lens across the entire array can provide improved elevational resolution at a fixed focal distance. Unfortunately, this compromises resolution before and after the elevational focal zone due to partial volume averaging.
focusing can produce smaller slice thickness over a range of tissue depths. A disadvantage of elevational focusing is a frame rate reduction penalty required for multiple excitations to build one image. The increased width of the transducer array also limits positioning flexibility. Extension to full 2D transducer arrays with enhancements in computational power allows 3D imaging with more uniform resolution throughout the image volume.
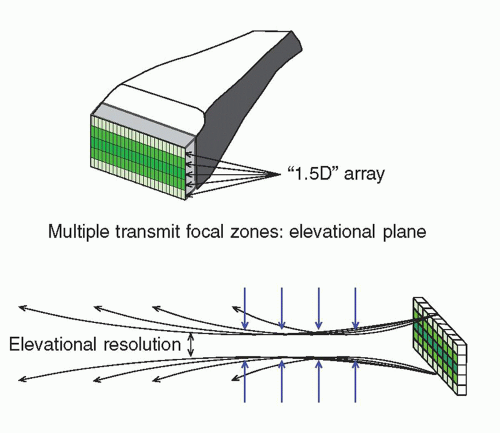 ▪ FIGURE 14-23 Elevational resolution with multiple transmit focusing zones is achieved with “1.5D” transducer arrays to reduce the slice-thickness profile over an extended depth. Five to seven rows of discrete arrays replace the single array. Phase delay timing provides focusing in the elevational plane, like that used for lateral transmit and receive focusing.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|