- The underlying principles of nuclear medicine imaging and therapy
- The biological aspects of nuclear medicine
- External dosimetry issues specific to nuclear medicine
- Internal dosimetry in nuclear medicine
- The medical internal radiation dosimetry (MIRD) method
Introduction
Nuclear medicine is a branch of radiology that uses radioactive pharmaceuticals in the diagnosis and treatment of patients. Radioactive pharmaceuticals or “radiopharmaceuticals” are usually compounds that have been labeled with a radioactive nuclide. The pharmaceutical properties of a radiopharmaceutical determine where the material will localize within the patient. The photons or electrons emitted by the radiopharmaceutical during radioactive decay are used to either provide information regarding the patient’s physiology or to deliver a therapeutic radiation dose to tissue. The risk of detrimental effects due to nuclear medicine exams is comparable with those from other modalities such as computed tomography (CT) and intervention radiology.
The route of administration of the radiopharmaceutical depends on the particular procedure. In most nuclear medicine procedures, the radiopharmaceutical is administered by intravenous injection. Some procedures require the radiopharmaceutical to be inhaled, ingested with food or liquid, or injected into regions of the body other than a vein.
The majority of nuclear medicine procedures are for diagnostic rather than therapeutic purposes. In diagnostic nuclear medicine, the biological distribution of the radiopharmaceutical within the patient is used for diagnosis. This “biodistribution” of the radiopharmaceutical depends on the physiologic processes occurring within the patient. The biodistribution of a radiopharmaceutical should be different between a normal patient and a patient with a disease. The different biodistribution between normal and diseased states should register as a difference on nuclear medicine images.
Nuclear medicine imaging can be done in a variety of ways. These include planar studies that are analogous to radiographs. Tomographic nuclear medicine studies are performed with single-photon emission computed tomography (SPECT) and positron emission tomography (PET). Regardless of the specific method used to obtain the images, the basic work flow remains the same. The radiopharmaceutical is administered to the patient. Images are acquired of the radiopharmaceutical within the patient. The images of the biodistribution of the radiopharmaceutical within the patient are then used for diagnosis.
Nuclear medicine therapy involves the use of radiopharmaceuticals that are selectively taken up in diseased tissue and emit high-energy electrons during beta-minus decay. These high-energy electrons have an average range in tissue of less than a centimeter. Thus, the radiopharmaceutical can deliver a large amount of energy to the diseased tissue.
Isotopes and Radiopharmaceuticals
The nucleus of an atom contains protons and neutrons. These particles are collectively known as nucleons. In standard nomenclature, the symbol for a generic element is 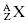 . In this notation, the atomic number, Z, is the number of protons in the nucleus. The atomic mass, A, is the total number of nucleons in the nucleus. For example,
. In this notation, the atomic number, Z, is the number of protons in the nucleus. The atomic mass, A, is the total number of nucleons in the nucleus. For example, 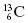 signifies that the carbon nucleus has a total of 13 nucleons. Six of these nucleons are protons. By subtracting Z from A, we find there are seven neutrons in the
signifies that the carbon nucleus has a total of 13 nucleons. Six of these nucleons are protons. By subtracting Z from A, we find there are seven neutrons in the 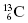 nucleus. Often, the number of protons is not written since the chemical symbol implies the number of protons. For instance,
nucleus. Often, the number of protons is not written since the chemical symbol implies the number of protons. For instance, 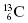 is usually written as 13C. All carbon nuclei have six protons. Another widely used nomenclature is the element followed by a hyphen and the atomic mass. For instance, 13C can also be written as C-13.
is usually written as 13C. All carbon nuclei have six protons. Another widely used nomenclature is the element followed by a hyphen and the atomic mass. For instance, 13C can also be written as C-13.
Isotopes of an element have the same number of protons, Z, but different numbers of neutrons. The number of protons in the nucleus determines the number of electrons in the outer shells. The electron structure of an atom determines its chemical properties. Thus, all isotopes of an element have the same chemical properties. The difference between isotopes is in the number of neutrons within the nucleus. Among isotopes of a given element, the nuclear properties can be significantly different. For example, isotopes of carbon include 11C, 12C, 13C, and 14C. All of these isotopes of carbon have six protons and six electrons and have the same chemical properties. The nuclear properties of these isotopes are very different. The isotopes 12C and 13C are stable while 11C and 14C are radioactive.
The nucleus of a radioactive element has too much energy and is unstable. The nucleus can change to a more stable state by undergoing radioactive decay and emitting particles and energy. Radioactive decay products include alpha particles, electrons, positrons, and gamma photons. Radionuclides used in nuclear medicine decay by gamma emission, beta-minus, electron capture, or positron decay. Radionuclides that emit alpha or neutrons are not used in nuclear medicine.
In nuclear medicine, radioactive nuclei are used to radiolabel molecules. For example, if one were to take glucose and replace some of the stable carbon atoms with a radioactive version such as 11C, then one would have a radioactive version of glucose that would have the same chemical behavior as normal glucose. The radioactive glucose could potentially be used as a tracer to study glucose uptake and metabolism in a patient. There is a wide variety of methods that can be used to add a radioactive atom to a molecule. As a result, there is a large arsenal of imaging agents that have been developed over the decades since the introduction of nuclear medicine imaging.
Gamma rays are high-energy, electromagnetic radiation. A particle or “quantum” of electromagnetic radiation is the photon. Gamma photons have zero charge and zero mass. The difference between X-ray photons and gamma photons is the point of origin. X-rays are produced from electron reactions, and gamma photons originate in nuclear reactions. The interaction of high-energy photons with matter is the same for both X-rays and gamma rays. In other words, X-rays and gamma rays undergo photoelectric absorption and Compton scattering.
The radionuclides used in nuclear medicine imaging emit gamma photons with specific, characteristic energies. For example, the most widely used radionuclide in nuclear medicine imaging is technetium-99m, Tc-99m or 99mTc. The “m” means that the nuclide is “metastable.” A Tc-99m nucleus will undergo radioactive decay to Tc-99 by emitting a gamma photon. After the emission of the gamma photon, the nucleus is left in the “ground” or lowest energy state. The energy of the photon emitted by the transition of Tc-99m to Tc-99 is 140 keV (Table 13.1). Scattering of the emitted photons within the patient leads to a spread in the energies emitted from the patient. Photons with energies corresponding to the primary emitted energy are used to form the images. Scattered photons contribute to image noise.
Table 13.1 Listed Are Several Radionuclides Commonly Used in Nuclear Medicine
| Radionuclide | Energy of Gamma Emission (keV) |
|---|---|
| Tc-99m | 140 |
| F-18 | 511 |
| Xe-133 | 81 |
| In-111 | 172, 247 |
| I-131 | 364 (also emits β-) |
| I-123 | 159 |
Radionuclides that undergo radioactive decay by gamma emission produce gamma rays with characteristic energies.
Some radionuclides used in nuclear medicine decay by beta-minus decay. In this type of decay, the emitted particles are an electron and an antineutrino. The antineutrino will likely not interact with tissue and will leave the patient. However, the electron will interact with the tissue. An electron has a relatively low mass and is negatively charged. Electrons emitted by radionuclides used in nuclear medicine will typically slow and stop in less than a centimeter of tissue. The energy transferred to the surrounding tissue by the slowing electron can be relatively large. In therapy, the goal is to use this energy to destroy diseased cells.
When a radionuclide undergoes beta-minus decay, a neutron is effectively converted into a proton. As a result, beta-minus decay does not change the atomic mass, A, of the decaying nucleus. Beta-minus decay increases the atomic number, Z, by 1. In the following reaction notation, X signifies the original, parent nucleus and Y is the resulting daughter nucleus. In beta-minus decay, the increase in the number of protons in the nucleus results in an element that is different from the parent element.
Beta-minus decay:
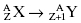
Beta-plus decay is also known as positron decay. In this decay, the emitted particles are an energetic positron and a neutrino. A positron is a positive electron and is the antiparticle of the electron. Sometimes the positron is written as β+. Beta-plus or positron decay effectively converts a proton into a neutron. As a result the atomic mass, A, remains unchanged and the atomic number, Z, decreases by 1.
Beta-plus decay:
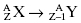
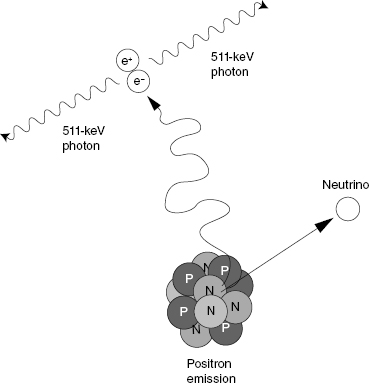
When a positron and electron interact, they undergo annihilation and emit two photons. The photons move away from each other in opposite directions, and each of these annihilation photons has 511 keV in energy. The energy of the reaction is carried away from the point of annihilation by the two photons. This characteristic feature of positron-electron annihilation is the basis for PET imaging (Fig. 13.1).
Figure 13.1 When a positron slows in matter, it will eventually interact with an electron. The result is a positron-electron annihilation event. The two particles are converted into two photons. Each photon has an energy of 511 keV. The photons move in opposite directions. This reaction is the basis for positron emission tomography (PET).
An alternative reaction to beta-plus decay is electron capture. In this type of decay, the nucleus captures a K-shell electron and emits a neutrino. In this reaction, a proton is effectively converted to a neutron. The capture of the K-shell electron by the nucleus leaves a vacancy in the K-shell. Subsequent filling of this vacancy by outer shell electrons produces characteristic X-rays and Auger electrons. After electron capture, the nucleus may be left in an excited state. The nucleus may then de-excite by gamma emission. Some medical radionuclides such as I-123 and Tl-201 decay by electron capture.
Radioactive Decay
Radioactive decay is a random process. It is impossible to predict exactly when a specific radioactive nucleus will undergo radioactive decay. However, statistical methods can be used to describe the behavior of large groups of radioactive nuclei. For a collection of radioactive nuclei, the “activity” is a quantity that describes the number of radioactive decays occurring at a certain point in time. The activity can be defined as
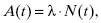
where A(t) is the activity at time t. The factor N(t) is the number of radioactive nuclei present at time t. The activity of a radioactive material exponentially decreases with time. The rate at which the exponential decay occurs is governed by the decay constant, λ. The decay constant, λ, is a unique value for each nuclide. The rate of decay is not affected by temperature, pressure, and electrical or magnetic fields. The Système International (SI) unit for activity is the becquerel (Bq), which is equal to 1 disintegration per second. In the United States, the common unit of activity is the curie. One curie is equivalent to 3.7 × 1010 disintegrations per second.
Units of activity:
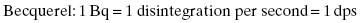
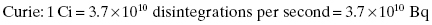
The following exponential equation is known as the decay equation and describes how the activity changes with time:
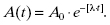
Here, A0 is the initial activity of the sample at an arbitrary time, t = 0. This time is often referred to as the calibration time. The term A(t) is the activity at a time, t, subsequent to the calibration time.
It is common to refer to the half-life of a radionuclide. The half-life is the time for half of the radioactive nuclei present at time t = 0 to undergo radioactive decay. Each radioactive nuclide has a characteristic half-life. Table 13.2 shows the characteristic half-life of some of the most common radioactive nuclides used in nuclear medicine.
Table 13.2 Half-Lives for Several Radionuclides Commonly Used in Nuclear Medicine
| Radionuclide | Half-Life |
|---|---|
| Tc-99m | 6.02 hours |
| F-18 | 109 minutes |
| Xe-133 | 5.3 days |
| In-111 | 67 hours |
| I-131 | 8.06 days |
| I-123 | 13.2 hours |
Every radionuclide has a unique, characteristic half-life.
The half-life, T½, is equal to the natural logarithm of 2, ln(2), divided by the decay constant, λ:
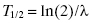
or
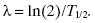
The decay equation is commonly written in terms of the half-life instead of the decay constant:

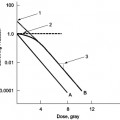
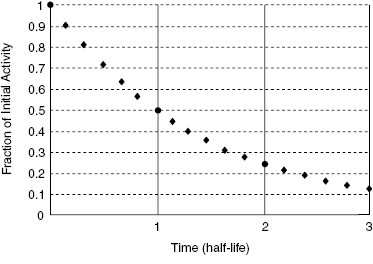
Figure 13.2 shows the activity of any radionuclide as a function time. In this case, the time is expressed as the number of half-lives that have passed since the initial time, t = 0. For example, if we have 20 mCi of Tc-99m in a vial at noon, what activity can we expect to have at midnight? The half-life of Tc-99m is 6 hours. After 12 hours, or two half-lives, only 25% of the initial radioactive nuclei will remain. Thus, at midnight, only 5 mCi of Tc-99m will remain in the vial.
Figure 13.2 The activity of a radioactive material plotted as a function of time. After one half-life, the activity will be 50% of the activity at time, t = 0. After two half-lives, the activity will be 25% of the initial activity.
The activity administered to a patient depends on the procedure. The amount of activity given to a patient may be modified by the physician to take into account the patient age, weight, metabolic status, and other factors that may affect the uptake and elimination of the radiopharmaceutical. Activities commonly administered in nuclear medicine range from a few microcuries, μCi, to a few hundred millicuries, mCi. Most imaging doses are in the neighborhood of 1–30 mCi. Some therapy doses can be up to several hundred millicuries. There is no upper limit to the amount of activity a nuclear medicine physician may prescribe for a patient. Like all medical procedures, the nuclear medicine physician must weigh the risk to the patient and the potential benefit to the patient from doing the procedure.
External Dosimetry
External dosimetry in nuclear medicine is limited to exposures from gamma rays or beta particles. Most instances of exposure are from gamma rays. Like X-rays, these are energetic photons. In matter, gamma ray photons are absorbed and scattered by the same mechanisms that act on X-rays, yet there are significant differences between X-ray-emitting sources and gamma-emitting sources that may impact external dosimetry.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree