regularization, which induces sparsity, in our integration method. We also introduce regularization to make the dense fields more adhering to cardiac biomechanics. Finally, we motivate the necessity of temporal coherence in the dense fields and demonstrate a way of doing so.
We test our method on ultrasound (US) images acquired from six open-chested canine hearts. Baseline and post-occlusion strain results are presented for an animal, where we were able to detect significant change in the ischemic region. Six sets of strain results were also compared to strains obtained from tagged magnetic resonance (MR) data. Median correlation (with MR-tagging) coefficients of 0.73 and 0.82 were obtained for radial and circumferential strains respectively.
Keywords
EchocardiographyMotionShape trackingSpeckle trackingRadial basis functionsRegularization1 Introduction
A reliable quantitative and qualitative assessment of the motion behavior can assist in the detection, localization, control and treatment of myocardial injuries. Within this context, echocardiography is a popular and important tool because it is relatively inexpensive and highly portable. It also provides better temporal resolution in comparison to other modalities.
Over the years several shape based tracking methods and speckle based tracking methods have been proposed to calculate dense motion field for the LV and ultimately calculate regional strains. Shape based methods track myocardial boundaries or automatically selected shape and intensity based features which predominantly arise from myocardial boundaries [1, 2]. Hence, mid-wall displacements are usually missing or not reliable.
Popular speckle tracking methods can be broadly classified into block-matching algorithms such as Lubinski et al. [3] and non-rigid registration based methods such as Heyde et al. [4]. Speckle tracking methods are better at estimating mid-wall displacements but do not always successfully track the boundaries due to inconsistent speckle patterns at the blood tissue interface.
Compas et al. [5] proposed a method to calculate dense field across the myocardium by integrating displacements from shape and speckle tracking methods using radial basis function (RBF) interpolation. The use of RBFs provided a flexible and simple framework by eliminating the need of complicated grids and meshes to model cardiac geometry. Hence, it provided a simpler mechanism of modeling complex, and sometimes incomplete, cardiac geometries.
In this work, we pose the problem in a Bayesian setting and then present it in a convex optimization format. We use 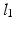 regularization to tackle noise and also, indirectly, to select features. Drawing inspiration from cardiac biomechanics, we add penalties on divergences and derivatives. We also motivate and demonstrate the need to make motion fields temporally coherent. We test our methods on 2D canine heart images and present appropriate results.
regularization to tackle noise and also, indirectly, to select features. Drawing inspiration from cardiac biomechanics, we add penalties on divergences and derivatives. We also motivate and demonstrate the need to make motion fields temporally coherent. We test our methods on 2D canine heart images and present appropriate results.
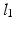 regularization to tackle noise and also, indirectly, to select features. Drawing inspiration from cardiac biomechanics, we add penalties on divergences and derivatives. We also motivate and demonstrate the need to make motion fields temporally coherent. We test our methods on 2D canine heart images and present appropriate results.
regularization to tackle noise and also, indirectly, to select features. Drawing inspiration from cardiac biomechanics, we add penalties on divergences and derivatives. We also motivate and demonstrate the need to make motion fields temporally coherent. We test our methods on 2D canine heart images and present appropriate results.2 Methods
We will first briefly discuss the elementary methods to obtain initial shape and speckle tracking based estimation. Then we will discuss in detail the integration framework where our contribution lies.
2.1 Elementary Motion Estimation Methods
Shape Tracking. We use boundary features derived from an automated level-set segmentation method [6]. Once endocardial and epicardial boundary points are found, a modified Generalized Robust Point Matching (GRPM) algorithm is used to obtain displacement estimates across frames [1].
The algorithm matches two point sets X and Y by solving for a fuzzy correspondence matrix m. The original form was solved using an iterative setup. However, since the objective function was convex, we determined that we could solve this directly using a convex optimization solver [7]. The GRPM formulation allowed us to control the relative weight between minimizing distance between the point sets and minimizing the difference in their shape characteristics such as curvatures. It also allowed us to control the fuzziness (or uniqueness) of the correspondence.
Speckle Tracking. Speckle patterns are inherent to US and, while they seem random in nature, they exhibit some consistency in a small time window. This can be leveraged and a correlation based tracking of local image patches is done.
For a pixel in a given image, a kernel of one speckle length around the pixel, in the complex signal, is correlated with neighboring kernels in the next frame [3]. The peak correlation value is used to determine the matching kernel in the next frame and calculate displacement and confidence measure. The velocity in the echo beam direction is further refined using zero-crossings of the phase of the complex correlation function.
2.2 Integration Framework
Bayesian Viewpoint. For an image frame, the dense displacement is U and the initial shape and speckle tracking displacements are 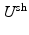 and
and 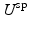 respectively. Conditioning using Bayes’ theorem, and assuming independence between
respectively. Conditioning using Bayes’ theorem, and assuming independence between 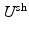 and
and 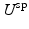 , we get
, we get
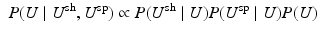
P(U) captures the assumptions we make about our displacement field as a prior. We assume that 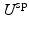 and
and 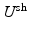 are both normally distributed with respect to U. Taking
are both normally distributed with respect to U. Taking 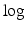 on both sides, we get:
on both sides, we get:
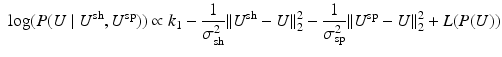
Here, the 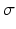 ’s are the standard deviations of the shape and speckle displacements. L(P(U)) is the log of the prior distribution on U. We obtain the final dense field by maximizing the log posterior.
’s are the standard deviations of the shape and speckle displacements. L(P(U)) is the log of the prior distribution on U. We obtain the final dense field by maximizing the log posterior.
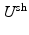 and
and 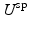 respectively. Conditioning using Bayes’ theorem, and assuming independence between
respectively. Conditioning using Bayes’ theorem, and assuming independence between 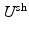 and
and 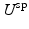 , we get
, we get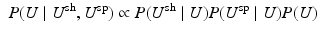
(1)
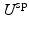 and
and 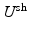 are both normally distributed with respect to U. Taking
are both normally distributed with respect to U. Taking 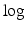 on both sides, we get:
on both sides, we get: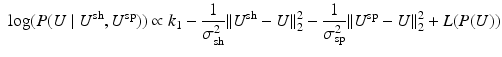
(2)
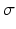 ’s are the standard deviations of the shape and speckle displacements. L(P(U)) is the log of the prior distribution on U. We obtain the final dense field by maximizing the log posterior.
’s are the standard deviations of the shape and speckle displacements. L(P(U)) is the log of the prior distribution on U. We obtain the final dense field by maximizing the log posterior.RBF Interpolation. An RBF is parametrized by its location  and its width
and its width 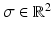 (in 2D). Hence, during an RBF interpolation process, different resolutions can be captured by altering the width and the number of RBFs. In our case, we place RBFs around the myocardium and use a multi-level scheme, where in each iteration RBFs of different widths and varying quantity are used [8].
(in 2D). Hence, during an RBF interpolation process, different resolutions can be captured by altering the width and the number of RBFs. In our case, we place RBFs around the myocardium and use a multi-level scheme, where in each iteration RBFs of different widths and varying quantity are used [8].
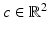 and its width
and its width 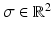 (in 2D). Hence, during an RBF interpolation process, different resolutions can be captured by altering the width and the number of RBFs. In our case, we place RBFs around the myocardium and use a multi-level scheme, where in each iteration RBFs of different widths and varying quantity are used [8].
(in 2D). Hence, during an RBF interpolation process, different resolutions can be captured by altering the width and the number of RBFs. In our case, we place RBFs around the myocardium and use a multi-level scheme, where in each iteration RBFs of different widths and varying quantity are used [8].For each iteration, first we evaluate the value of all the RBFs for consideration and consolidate them as a design matrix (or a dictionary of bases) H. Then, the displacement values are expressed as a linear combination of these bases as 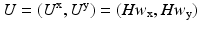 . Therefore, our goal is to solve for the linear weights
. Therefore, our goal is to solve for the linear weights 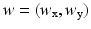 , which we accomplish using an optimization setup:
, which we accomplish using an optimization setup:
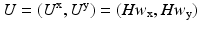 . Therefore, our goal is to solve for the linear weights
. Therefore, our goal is to solve for the linear weights 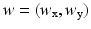 , which we accomplish using an optimization setup:
, which we accomplish using an optimization setup:
![$$\begin{aligned} \hat{w}_{\mathrm {x}}, \hat{w}_{\mathrm {y}} = \mathop {{{\mathrm{argmin}}}}\limits _{w_{\mathrm {x}}, w_{\mathrm {y}}} \sum _{i \in A_{\mathrm {sh}}}{c^{\mathrm {sh}}_i \left( [Hw]_i - U^{\mathrm {sh}}_i \right) ^2} + \sum _{i \in A_{\mathrm {sp}}}{c^{\mathrm {sp}}_i \left( [Hw]_i - U^{\mathrm {sp}}_i \right) ^2} \end{aligned}$$](/wp-content/uploads/2016/09/A339585_1_En_7_Chapter_Equ3.gif)