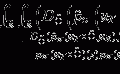Band designation
Approximate frequency range
Approximate wavelengths
HF (high frequency)
3–30 MHz
50 m
VHF (very high frequency)
30–300 MHz
5 m
UHF (ultrahigh frequency)
300–1,000 MHz
1 m
L-band
1–2 GHz
20 cm
S-band
2–4 GHz
10 cm
C-band
4–8 GHz
5 cm
X-band
8–12 GHz
3 cm
Ku-band (under K)
12–18 GHz
2 cm
K-band
18–27 GHz
1.5 cm
Ka-band (above K)
27–40 GHz
1 cm
mm-wave
40–300 GHz
5 mm
3 Mathematical Modeling
SAR relies on a number of very specific simplifying assumptions about radar scattering phenomenology and data-collection scenarios:
1.
Most imaging radar systems make use of the start–stop approximation [29], in which both the radar sensor and scattering object are assumed to be stationary during the time interval over which the pulse interacts with the target.
2.
The target or scene is assumed to behave as a rigid body.
3.
SAR imaging methods assume a linear relationship between the data and scene.
Scattering of Electromagnetic Waves
The present discussion considers only scattering from targets that are stationary.
For linear materials, Maxwell’s equations can be used [34] to obtain an inhomogeneous wave equation for the electric field 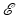 at time t and position x:
at time t and position x:
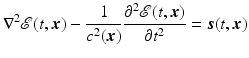
and a similar equation for the magnetic field 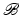 . Here
. Here 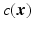 denotes the speed of propagation of the wave (throughout the atmosphere, this speed is approximately independent of position and equal to the constant vacuum speed c) and
denotes the speed of propagation of the wave (throughout the atmosphere, this speed is approximately independent of position and equal to the constant vacuum speed c) and 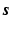 is a source term that, in general, can involve
is a source term that, in general, can involve 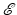 and
and 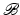 . For typical radar problems, the wave speed is constant in the region between the source and the scattering objects (targets) and varies only within the target volume. Consequently, here scattering objects are modeled solely via the source term
. For typical radar problems, the wave speed is constant in the region between the source and the scattering objects (targets) and varies only within the target volume. Consequently, here scattering objects are modeled solely via the source term 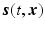 .
.
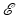 at time t and position x:
at time t and position x: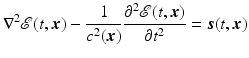
(1)
 . Here
. Here 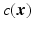 denotes the speed of propagation of the wave (throughout the atmosphere, this speed is approximately independent of position and equal to the constant vacuum speed c) and
denotes the speed of propagation of the wave (throughout the atmosphere, this speed is approximately independent of position and equal to the constant vacuum speed c) and 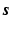 is a source term that, in general, can involve
is a source term that, in general, can involve 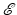 and
and 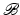 . For typical radar problems, the wave speed is constant in the region between the source and the scattering objects (targets) and varies only within the target volume. Consequently, here scattering objects are modeled solely via the source term
. For typical radar problems, the wave speed is constant in the region between the source and the scattering objects (targets) and varies only within the target volume. Consequently, here scattering objects are modeled solely via the source term 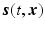 .
.One Cartesian component of Eq. (1) is
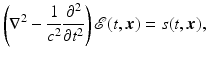
where atmospheric propagation between source and target has been assumed.
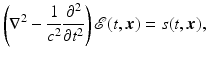
(2)
Basic Facts About the Wave Equation
A fundamental solution [69] of the inhomogeneous wave equation is a generalized function [30, 69] satisfying
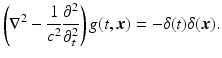
The solution of (3) that is useful is
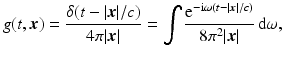
where in the second equality the identity
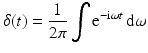
was used. The function 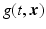 can be physically interpreted as the field at
can be physically interpreted as the field at 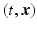 due to a source at the origin
due to a source at the origin 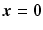 at time t = 0 and is called the outgoing fundamental solution or (outgoing) Green’s function.
at time t = 0 and is called the outgoing fundamental solution or (outgoing) Green’s function.
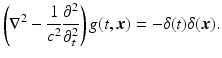
(3)
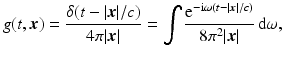
(4)
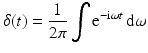
(5)
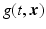 can be physically interpreted as the field at
can be physically interpreted as the field at 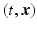 due to a source at the origin
due to a source at the origin  at time t = 0 and is called the outgoing fundamental solution or (outgoing) Green’s function.
at time t = 0 and is called the outgoing fundamental solution or (outgoing) Green’s function.The Green’s function [62] can be used to solve the constant-speed wave equation with any source term. In particular, the outgoing solution of
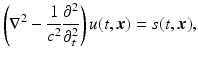
is
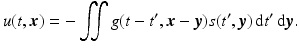
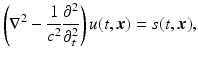
(6)
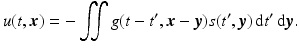
(7)
Basic Scattering Theory
In constant-wave velocity radar problems, the source 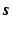 is a sum of two terms,
is a sum of two terms, 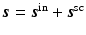 , where
, where 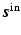 models the transmitting antenna and
models the transmitting antenna and 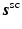 models the scattering object. The solution
models the scattering object. The solution  to Eq. (1), which is written as
to Eq. (1), which is written as 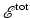 , therefore splits into two parts:
, therefore splits into two parts: 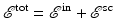 . The first term,
. The first term, 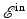 , satisfies the wave equation for the known, prescribed source
, satisfies the wave equation for the known, prescribed source 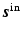 . This part is called the incident field, because it is incident upon the scatterers. The second term,
. This part is called the incident field, because it is incident upon the scatterers. The second term, 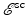 , is due to target scattering, and this part is called the scattered field. We use the same decomposition in the simplified scalar model.
, is due to target scattering, and this part is called the scattered field. We use the same decomposition in the simplified scalar model.
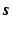 is a sum of two terms,
is a sum of two terms, 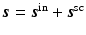 , where
, where 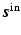 models the transmitting antenna and
models the transmitting antenna and 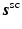 models the scattering object. The solution
models the scattering object. The solution 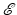 to Eq. (1), which is written as
to Eq. (1), which is written as 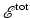 , therefore splits into two parts:
, therefore splits into two parts: 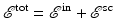 . The first term,
. The first term, 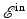 , satisfies the wave equation for the known, prescribed source
, satisfies the wave equation for the known, prescribed source 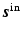 . This part is called the incident field, because it is incident upon the scatterers. The second term,
. This part is called the incident field, because it is incident upon the scatterers. The second term, 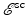 , is due to target scattering, and this part is called the scattered field. We use the same decomposition in the simplified scalar model.
, is due to target scattering, and this part is called the scattered field. We use the same decomposition in the simplified scalar model.One approach to finding the scattered field is to simply solve (2) directly, using, for example, numerical time-domain techniques. For many purposes, however, it is convenient to reformulate the scattering problem in terms of an integral equation.
The Lippmann–Schwinger Integral Equation
In scattering problems the source term 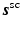 (typically) represents the target’s response to an incident field. This part of the source function will generally depend on the geometric and material properties of the target and on the form and strength of the incident field. Consequently,
(typically) represents the target’s response to an incident field. This part of the source function will generally depend on the geometric and material properties of the target and on the form and strength of the incident field. Consequently, 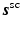 can be quite complicated to describe analytically, and in general, it will not have the same direction as
can be quite complicated to describe analytically, and in general, it will not have the same direction as 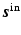 . Fortunately, for this article, it is not necessary to provide a detailed analysis of the target’s response; for stationary objects consisting of linear materials, the scalar model s sc is written as the time-domain convolution
. Fortunately, for this article, it is not necessary to provide a detailed analysis of the target’s response; for stationary objects consisting of linear materials, the scalar model s sc is written as the time-domain convolution
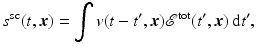
where 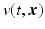 is called the reflectivity function and depends on target orientation. In general, this function also accounts for polarization effects.
is called the reflectivity function and depends on target orientation. In general, this function also accounts for polarization effects.
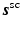 (typically) represents the target’s response to an incident field. This part of the source function will generally depend on the geometric and material properties of the target and on the form and strength of the incident field. Consequently,
(typically) represents the target’s response to an incident field. This part of the source function will generally depend on the geometric and material properties of the target and on the form and strength of the incident field. Consequently, 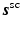 can be quite complicated to describe analytically, and in general, it will not have the same direction as
can be quite complicated to describe analytically, and in general, it will not have the same direction as 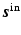 . Fortunately, for this article, it is not necessary to provide a detailed analysis of the target’s response; for stationary objects consisting of linear materials, the scalar model s sc is written as the time-domain convolution
. Fortunately, for this article, it is not necessary to provide a detailed analysis of the target’s response; for stationary objects consisting of linear materials, the scalar model s sc is written as the time-domain convolution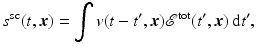
(9)
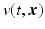 is called the reflectivity function and depends on target orientation. In general, this function also accounts for polarization effects.
is called the reflectivity function and depends on target orientation. In general, this function also accounts for polarization effects.The Lippmann–Schwinger Equation in the Frequency Domain
In the frequency domain, the electric field and reflectivity function become
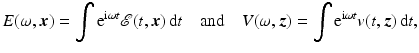
respectively. Thus the frequency-domain version of (2) is
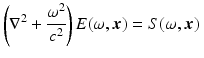
and of (10) is
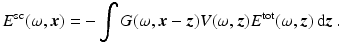
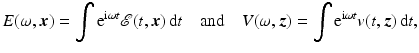
(11)
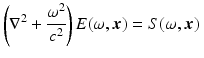
(12)
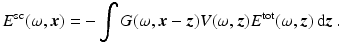
(13)
The reflectivity function 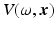 can display a sensitive dependence on ω [34, 36, 53]. When the target is small in comparison with the wavelength of the incident field, for example, V is proportional to ω 2 (this behavior is known as “Rayleigh scattering”). At higher frequencies (shorter wavelengths), the dependence on ω is typically less pronounced. In the so-called optical region,
can display a sensitive dependence on ω [34, 36, 53]. When the target is small in comparison with the wavelength of the incident field, for example, V is proportional to ω 2 (this behavior is known as “Rayleigh scattering”). At higher frequencies (shorter wavelengths), the dependence on ω is typically less pronounced. In the so-called optical region, 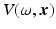 is often approximated as being independent of ω (see, however, [56]); the optical approximation is used in this chapter, and the ω dependence is simply dropped. In the time domain, this corresponds to
is often approximated as being independent of ω (see, however, [56]); the optical approximation is used in this chapter, and the ω dependence is simply dropped. In the time domain, this corresponds to 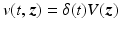 , and the delta function can be used to carry out the t ′ integration in (10).
, and the delta function can be used to carry out the t ′ integration in (10).
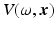 can display a sensitive dependence on ω [34, 36, 53]. When the target is small in comparison with the wavelength of the incident field, for example, V is proportional to ω 2 (this behavior is known as “Rayleigh scattering”). At higher frequencies (shorter wavelengths), the dependence on ω is typically less pronounced. In the so-called optical region,
can display a sensitive dependence on ω [34, 36, 53]. When the target is small in comparison with the wavelength of the incident field, for example, V is proportional to ω 2 (this behavior is known as “Rayleigh scattering”). At higher frequencies (shorter wavelengths), the dependence on ω is typically less pronounced. In the so-called optical region, 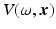 is often approximated as being independent of ω (see, however, [56]); the optical approximation is used in this chapter, and the ω dependence is simply dropped. In the time domain, this corresponds to
is often approximated as being independent of ω (see, however, [56]); the optical approximation is used in this chapter, and the ω dependence is simply dropped. In the time domain, this corresponds to 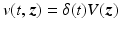 , and the delta function can be used to carry out the t ′ integration in (10).
, and the delta function can be used to carry out the t ′ integration in (10).The Born Approximation
For radar imaging, the field 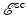 is measured at the radar antenna, and from these measurements, the goal is to determine V. However, both V and
is measured at the radar antenna, and from these measurements, the goal is to determine V. However, both V and 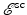 in the neighborhood of the target are unknown, and in (10) these unknowns are multiplied together. This nonlinearity makes it difficult to solve for V. Consequently, almost all work on radar imaging relies on the Born approximation, which is also known as the weak-scattering or single-scattering approximation [38, 47]. The Born approximation replaces
in the neighborhood of the target are unknown, and in (10) these unknowns are multiplied together. This nonlinearity makes it difficult to solve for V. Consequently, almost all work on radar imaging relies on the Born approximation, which is also known as the weak-scattering or single-scattering approximation [38, 47]. The Born approximation replaces 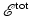 on the right side of (10) by
on the right side of (10) by 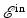 , which is known. This results in a linear formula for
, which is known. This results in a linear formula for 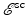 in terms of V:
in terms of V:
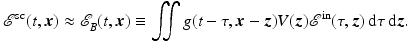
In the frequency domain, the Born approximation is
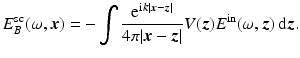
The Born approximation is very useful because it makes the imaging problem linear. It is not, however, always a good approximation; see Sect. 6.
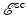 is measured at the radar antenna, and from these measurements, the goal is to determine V. However, both V and
is measured at the radar antenna, and from these measurements, the goal is to determine V. However, both V and 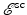 in the neighborhood of the target are unknown, and in (10) these unknowns are multiplied together. This nonlinearity makes it difficult to solve for V. Consequently, almost all work on radar imaging relies on the Born approximation, which is also known as the weak-scattering or single-scattering approximation [38, 47]. The Born approximation replaces
in the neighborhood of the target are unknown, and in (10) these unknowns are multiplied together. This nonlinearity makes it difficult to solve for V. Consequently, almost all work on radar imaging relies on the Born approximation, which is also known as the weak-scattering or single-scattering approximation [38, 47]. The Born approximation replaces 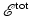 on the right side of (10) by
on the right side of (10) by 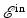 , which is known. This results in a linear formula for
, which is known. This results in a linear formula for 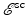 in terms of V:
in terms of V: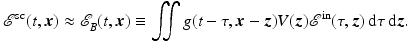
(14)
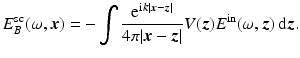
(15)
The Incident Field
The incident field 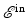 is obtained by solving (2), where s in is taken to be the relevant component of the current density on the source antenna and s sc is zero. This article uses a simplified point-like antenna model, for which
is obtained by solving (2), where s in is taken to be the relevant component of the current density on the source antenna and s sc is zero. This article uses a simplified point-like antenna model, for which 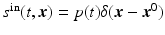 , where p is the waveform transmitted by the antenna. Typically p consists of a sequence of time-shifted pulses, so that
, where p is the waveform transmitted by the antenna. Typically p consists of a sequence of time-shifted pulses, so that 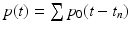 .
.
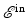 is obtained by solving (2), where s in is taken to be the relevant component of the current density on the source antenna and s sc is zero. This article uses a simplified point-like antenna model, for which
is obtained by solving (2), where s in is taken to be the relevant component of the current density on the source antenna and s sc is zero. This article uses a simplified point-like antenna model, for which 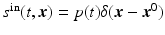 , where p is the waveform transmitted by the antenna. Typically p consists of a sequence of time-shifted pulses, so that
, where p is the waveform transmitted by the antenna. Typically p consists of a sequence of time-shifted pulses, so that 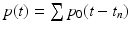 .
.Model for the Scattered Field
In monostatic radar systems, the transmit and receive antennas are colocated – often the same antenna is used. Use of (17) in (15) shows that the Born-approximated scattered field at the transmitter location 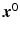 is
is
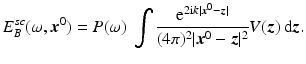
Fourier transforming (18) results in an expression for the time-domain field:
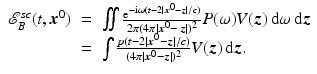
Under the Born approximation, the scattered field is a superposition of scattered fields from point-like targets 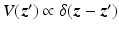 .
.
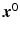 is
is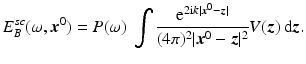
(18)
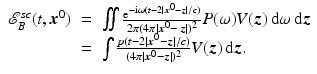
(19)
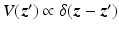 .
. The Matched Filter
An important aspect of (19) is the 1∕R 2 geometrical decay (where 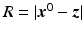 ). When R is large (which it usually is), this decay factor results in a received signal that is extremely small – so small, in fact, that it can be dominated by thermal noise in the receiver. Thus it is difficult even to detect the presence of a target. Target detection is typically accomplished by means of a matched filter [19, 25, 50].
). When R is large (which it usually is), this decay factor results in a received signal that is extremely small – so small, in fact, that it can be dominated by thermal noise in the receiver. Thus it is difficult even to detect the presence of a target. Target detection is typically accomplished by means of a matched filter [19, 25, 50].
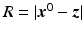 ). When R is large (which it usually is), this decay factor results in a received signal that is extremely small – so small, in fact, that it can be dominated by thermal noise in the receiver. Thus it is difficult even to detect the presence of a target. Target detection is typically accomplished by means of a matched filter [19, 25, 50].
). When R is large (which it usually is), this decay factor results in a received signal that is extremely small – so small, in fact, that it can be dominated by thermal noise in the receiver. Thus it is difficult even to detect the presence of a target. Target detection is typically accomplished by means of a matched filter [19, 25, 50].Below the matched filter is derived for scattering from a single fixed, point-like target. For such a target, by Eqs. (9) and (19), the signal scattered is simply a time-delayed version of the transmitted waveform:
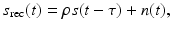 where τ corresponds to the 2R∕c delay, ρ is a proportionality factor related to the scatterer reflectivity V (z) and the geometric decay
where τ corresponds to the 2R∕c delay, ρ is a proportionality factor related to the scatterer reflectivity V (z) and the geometric decay 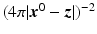 , and n denotes noise.
, and n denotes noise.
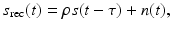
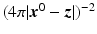 , and n denotes noise.
, and n denotes noise.The strategy is to apply a filter (convolution operator) to s rec in order to improve the signal-to-noise ratio. The filter’s impulse response (convolution kernel) is denoted by h, which implies that the filter output is
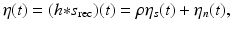
where
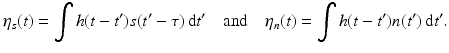 The signal output η s (τ) at time τ should be as large as possible, relative to the noise output η n (τ).
The signal output η s (τ) at time τ should be as large as possible, relative to the noise output η n (τ).
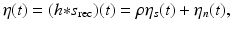
(20)
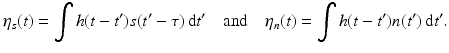
The noise is modeled as a random process. Thermal noise in the receiver is well approximated by white noise, which means that 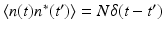 , where N corresponds to the noise power and
, where N corresponds to the noise power and 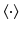 denotes expected value. Since the noise is random, so is η n . Thus the signal-to-noise (SNR) ratio to be maximized is
denotes expected value. Since the noise is random, so is η n . Thus the signal-to-noise (SNR) ratio to be maximized is
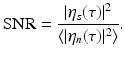
First, the denominator of (21) is
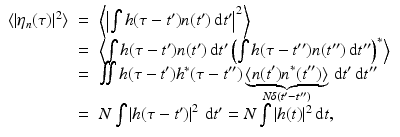 where in the last line the change of variables t = τ − t ′ has been made and where the star denotes complex conjugation. Thus (21) becomes
where in the last line the change of variables t = τ − t ′ has been made and where the star denotes complex conjugation. Thus (21) becomes
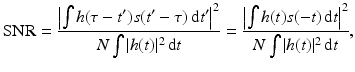
where in the numerator the change of variables t = τ − t ′ has been made. To the numerator of (22), the Cauchy–Schwarz inequality can be used to conclude that the numerator, and therefore the quotient (22), is maximized when h is chosen, so that
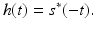 This is the impulse response of the matched filter. Thus to obtain the best signal-to-noise ratio, the received signal should be convolved with the time-reversed, complex-conjugated version of the expected signal.
This is the impulse response of the matched filter. Thus to obtain the best signal-to-noise ratio, the received signal should be convolved with the time-reversed, complex-conjugated version of the expected signal.
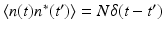 , where N corresponds to the noise power and
, where N corresponds to the noise power and  denotes expected value. Since the noise is random, so is η n . Thus the signal-to-noise (SNR) ratio to be maximized is
denotes expected value. Since the noise is random, so is η n . Thus the signal-to-noise (SNR) ratio to be maximized is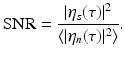
(21)
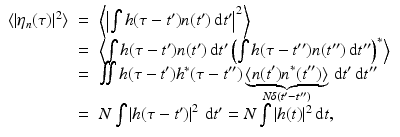
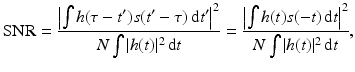
(22)
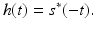
With this choice, the filter (20) can be written as
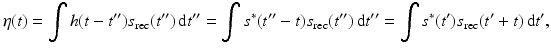
which is a correlation between s and s rec. If s = s rec, (23) is called an autocorrelation . Radar receivers which perform this kind of signal processing are known as “correlation receivers.”
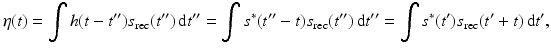
(23)
The Effect of Matched Filtering on Radar Data
The Small-Scene Approximation
The small-scene approximation, namely,
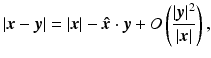
where  denotes a unit vector in the direction
denotes a unit vector in the direction  and is often applied to situations in which the scene to be imaged is small in comparison with its average distance from the radar. This approximation is valid for
and is often applied to situations in which the scene to be imaged is small in comparison with its average distance from the radar. This approximation is valid for 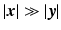 .
.
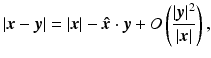
(25)
 denotes a unit vector in the direction
denotes a unit vector in the direction  and is often applied to situations in which the scene to be imaged is small in comparison with its average distance from the radar. This approximation is valid for
and is often applied to situations in which the scene to be imaged is small in comparison with its average distance from the radar. This approximation is valid for 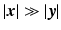 .
.Use of (25) in (4) gives rise to the large-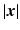 expansion of the Green’s function: [12, 19]
expansion of the Green’s function: [12, 19]
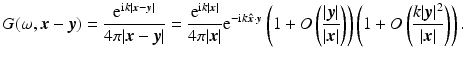
Here, the first-order term must be included in the exponential because 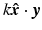 can take on values that are large fractions of 2π.
can take on values that are large fractions of 2π.
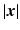 expansion of the Green’s function: [12, 19]
expansion of the Green’s function: [12, 19]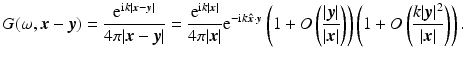
(26)
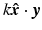 can take on values that are large fractions of 2π.
can take on values that are large fractions of 2π.Small-Scene, Matched-Filtered Radar Data
In (19), the origin of coordinates can be chosen to be in or near the target, and then the small-scene expansion (26) (with 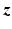 playing the role of y) can be used in the matched-filtered version of (19). This results in the expression for the matched-filtered data:
playing the role of y) can be used in the matched-filtered version of (19). This results in the expression for the matched-filtered data:
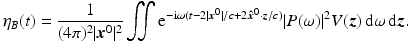
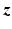 playing the role of y) can be used in the matched-filtered version of (19). This results in the expression for the matched-filtered data:
playing the role of y) can be used in the matched-filtered version of (19). This results in the expression for the matched-filtered data: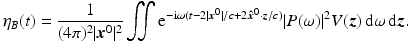
(27)
Thus we see that each frequency component of the data provides us with a Fourier component of the reflectivity V.
The Range Profile
Signals with large bandwidth are commonly used in synthetic aperture imaging. When the bandwidth is large, the pulse p is said to be a high-range-resolution (HRR) pulse . An especially simple large-bandwidth signal is one for which | P(ω) | 2 is constant over its support. In this case, the ω-integral in Eq. (27) reduces to a scaled sinc(t) function centered on
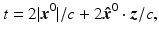 and the width of this sinc function is inversely proportional to the bandwidth. When the support of | P(ω) | 2 is infinite, of course, this sinc(t) becomes a delta function. Thus large-bandwidth (HRR), matched-filtered data can be approximated by
and the width of this sinc function is inversely proportional to the bandwidth. When the support of | P(ω) | 2 is infinite, of course, this sinc(t) becomes a delta function. Thus large-bandwidth (HRR), matched-filtered data can be approximated by
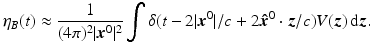
Since time delay and range are related in monostatic radar systems as t = 2R∕c, Eq. (29) can be seen to be a relation between the radar data η B (t) and the integral of the target reflectivity function over the plane
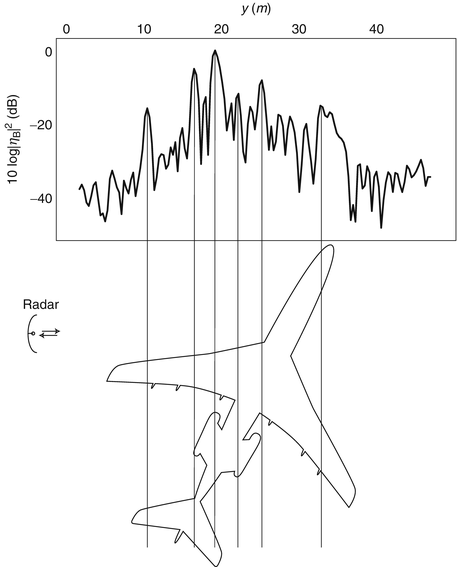
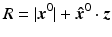 (with respect to the radar). Such data are said to form a “range profile” of the target. An example of an HRR range profile is displayed in Fig. 1.
(with respect to the radar). Such data are said to form a “range profile” of the target. An example of an HRR range profile is displayed in Fig. 1.
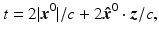
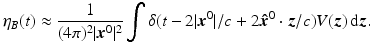
(29)
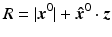

Fig. 1
Example of an HRR range profile of an aircraft (orientation displayed in inset)
4 Survey on Mathematical Analysis of Methods
The mathematical models discussed above assume that the target V (z) is stationary during its interaction with a radar pulse. However, synthetic aperture imaging techniques assume that the target moves with respect to the radar between pulses.
Inverse Synthetic Aperture Radar (ISAR)
A fixed radar system staring at a rotating target is equivalent (by change of reference frame) to a stationary target viewed by a radar moving (from pulse to pulse) on a circular arc. This circular arc will define, over time, a synthetic aperture, and sequential radar pulses can be used to sample those data that would be collected by a much larger radar antenna. Radar imaging based on such a data-collection configuration is known as inverse synthetic aperture radar (ISAR) imaging [5, 15, 41, 59, 66, 74]. This imaging scheme is typically used for imaging airplanes, spacecraft, and ships. In these cases, the target is relatively small and usually isolated.
Modeling Rotating Targets
The target reflectivity function in a frame fixed to the target is denoted by q. Then, as seen by the radar, the reflectivity function is 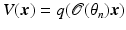 , where
, where 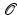 is an orthogonal matrix and where
is an orthogonal matrix and where 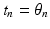 denotes the time at the start of the nth pulse of the sequence.
denotes the time at the start of the nth pulse of the sequence.
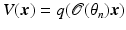 , where
, where 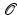 is an orthogonal matrix and where
is an orthogonal matrix and where 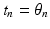 denotes the time at the start of the nth pulse of the sequence.
denotes the time at the start of the nth pulse of the sequence.For example, if the radar is in the plane perpendicular to the axis of rotation (so-called turntable geometry) , then the orthogonal matrix 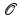 can be written as
can be written as
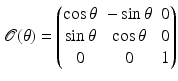
and 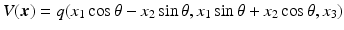 .
.
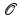 can be written as
can be written as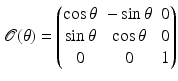
(30)
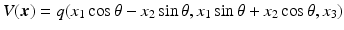 .
.Radar Data from Rotating Targets
The use of 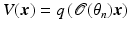 in (28) provides a model for the data from the n
in (28) provides a model for the data from the n




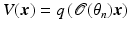 in (28) provides a model for the data from the n
in (28) provides a model for the data from the n
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


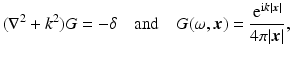
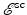
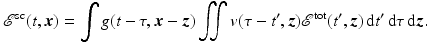
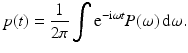
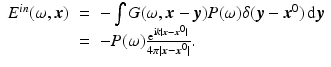
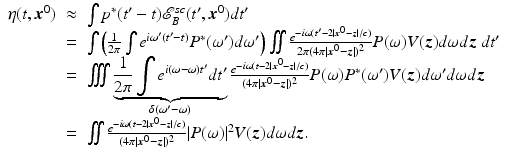
}. }$$](/wp-content/uploads/2016/04/A183156_2_En_49_Chapter_Equ29.gif)