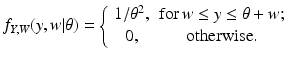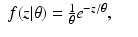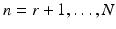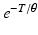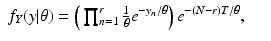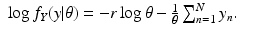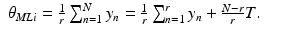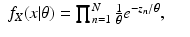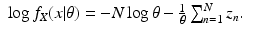The E-Step and M-Step
In statistical parameter estimation, one typically has an
observable random vector
Y taking values in
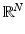
that is governed by a probability density function (pdf) or probability function (pf) of the form
f Y (
y |
θ), for some value of the parameter vector
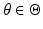
, where
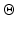
is the set of all legitimate values of
θ. Our
observed data consists of one realization
y of
Y; we do not exclude the possibility that the entries of
y are independently obtained samples of a common real-valued random variable. The true vector of parameters is to be estimated by maximizing the likelihood function
L y (
θ) =
f Y (
y |
θ) over all
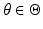
to obtain a maximum likelihood estimate,
θ ML .
To employ the EM algorithmic approach, it is assumed that there is another related random vector
X, which we shall call the
preferred data, such that, had we been able to obtain one realization
x of
X, maximizing the likelihood function
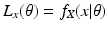
would have been simpler than maximizing the likelihood function
L y (
θ) =
f Y (
y |
θ). Of course, we do not have a realization
x of
X. The basic idea of the EM approach is to estimate
x using the current estimate of
θ, denoted
θ k , and to use each estimate
x k of
x to get the next estimate
θ k+1.
The EM algorithm proceeds in two steps. Having selected the preferred data
X, and having found
θ k , we form the function of
θ given by
this is the E-step of the EM algorithm. Then we maximize
Q(
θ |
θ k ) over all
θ to get
θ k+1; this is the M-step of the EM algorithm. In this way, the EM algorithm based on
X generates a sequence {
θ k } of parameter vectors.
For the discrete case of probability functions, we have
and for the continuous case of probability density functions, we have
In decreasing order of importance and difficulty, the goals are these:
1.
To have the sequence of parameters {θ k } converging to θ ML ;
2.
To have the sequence of functions
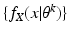
converging to
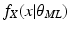
;
3.
To have the sequence of numbers
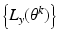
converging to
L y (
θ ML );
4.
To have the sequence of numbers
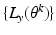
non-decreasing.
Our focus here is mainly on the fourth goal, with some discussion of the third goal. We do present some examples for which all four goals are attained. Clearly, the first goal requires a topology on the set
.
Difficulties with the Conventional Formulation
In [
1] we are told that
This is false; integrating with respect to
x gives one on the left side and 1∕
f Y (
y |
θ) on the right side. Perhaps the equation is not meant to hold for all
x, but just for some
x. In fact, if there is a function
h such that
Y =
h(
X), then Eq. (
14) might hold for those
x such that
h(
x) =
y. In fact, this is what happens in the discrete case of probabilities; in that case we do have
where
Consequently,
However, this modification of Eq. (
14) fails in the continuous case of probability density functions, since
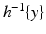
is often a subset of zero measure. Even if the set
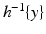
has positive measure, integrating both sides of Eq. (
14) over
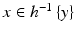
tells us that
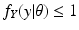
, which need not hold for probability density functions.
An Incorrect Proof
Everyone who works with the EM algorithm will say that the likelihood is non-decreasing for the EM algorithm. The proof of this fact usually proceeds as follows; we use the notation for the continuous case, but the proof for the discrete case is essentially the same. Use Eq. (
14) to get
Then replace the term
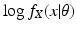
in Eq. (
13) with the right side of Eq. (
17), obtaining
Jensen’s Inequality tells us that
for any probability density functions
u(
x) and
v(
x). Since
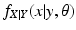
is a probability density function, we have
We conclude, therefore, that
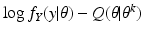
attains its minimum value at
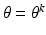
. Then we have
This proof is incorrect; clearly it rests on the validity of Eq. (
14), which is generally false. For the discrete case, with
Y =
h(
X), this proof is valid, when we use Eq. (
16), instead of Eq. (
14). In all other cases, however, the proof is incorrect.
Acceptable Data
We turn now to the question of how to repair the incorrect proof. Equation (
14) should read
for all
x. In order to replace
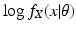
in Eq. (
13), we write
and
so that
We say that the preferred data is
acceptable if
that is, the dependence of
Y on
X is unrelated to the value of the parameter
θ. This definition provides our generalization of the relationship
Y =
h(
X).
When
X is acceptable, we have that
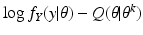
again attains its minimum value at
θ =
θ k . The assertion that the likelihood is non-decreasing then follows, using the same argument as in the previous incorrect proof.
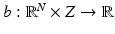 such that
such that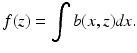
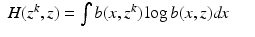
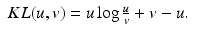
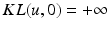 . The KL distance is extended to nonnegative vectors component-wise, so that for nonnegative vectors a and b, we have
. The KL distance is extended to nonnegative vectors component-wise, so that for nonnegative vectors a and b, we have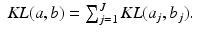
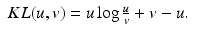
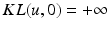 . The KL distance is extended to nonnegative vectors component-wise, so that for nonnegative vectors a and b, we have
. The KL distance is extended to nonnegative vectors component-wise, so that for nonnegative vectors a and b, we have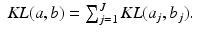
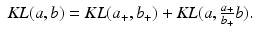
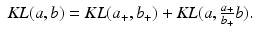
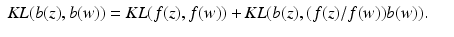
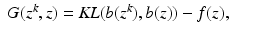
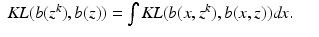
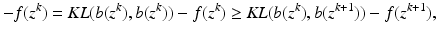
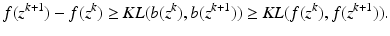
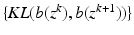
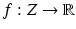
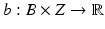
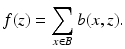
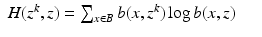
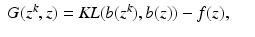
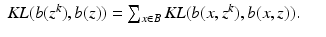
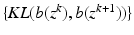
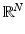
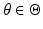
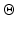
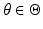
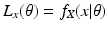
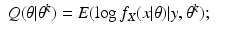
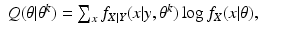
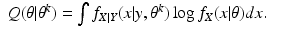
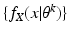
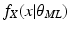
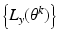
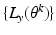
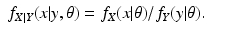
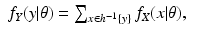
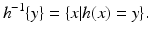
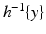
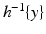
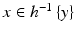
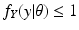
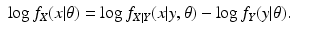
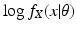
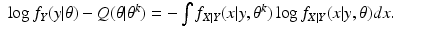
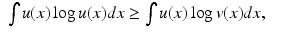
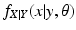
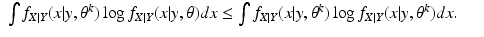
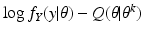
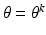
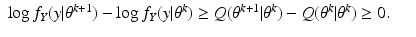
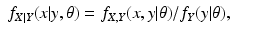
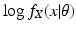
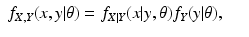
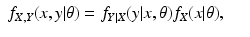
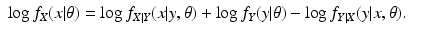
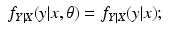
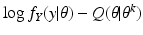
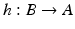
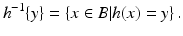
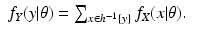
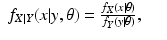
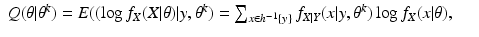
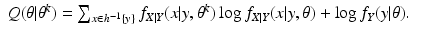
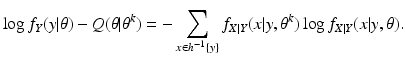
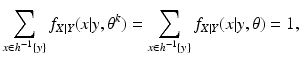
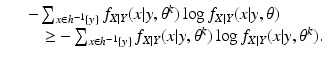
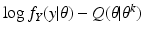
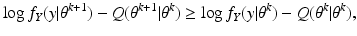
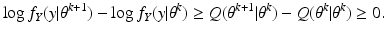
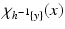
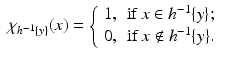
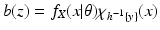
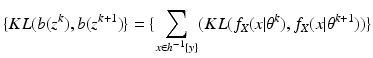
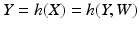
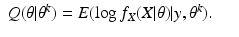
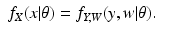
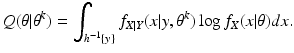
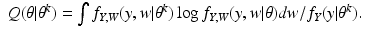
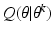
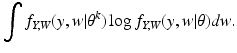
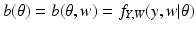
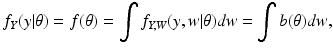
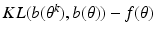
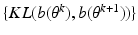
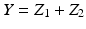
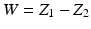
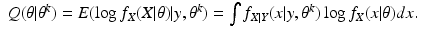
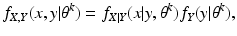
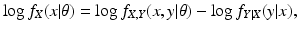
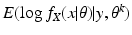
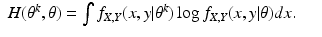
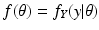
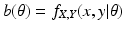
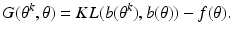
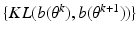
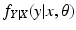
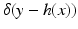
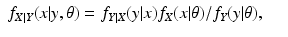
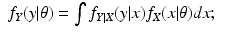
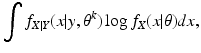
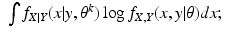
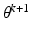
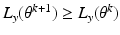
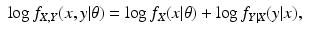
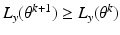
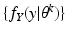
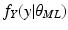
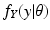
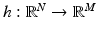
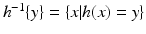
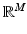
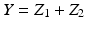
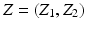
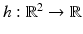
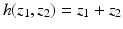
![$$\displaystyle\begin{array}{rcl} f_{Z}(z\vert \theta ) = f_{Z}(z_{1},z_{2}\vert \theta ) = \frac{1} {\theta ^{2}} \chi _{[0,\theta ]}(z_{1})\chi _{[0,\theta ]}(z_{2}).& &{}\end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_46_Chapter_Equ44.gif)
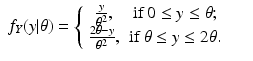
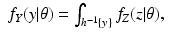
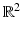
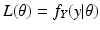
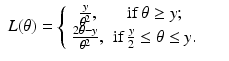
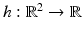
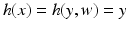
![$$\displaystyle\begin{array}{rcl} f_{Y }(y\vert \theta ) =\int \frac{1} {\theta ^{2}} \chi _{[0,\theta ]}(y - w)\chi _{[0,\theta ]}(w)dw.& &{}\end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_46_Chapter_Equ48.gif)