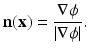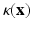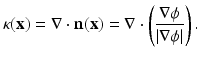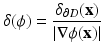, k = 1, …, K of different region-specific internal parameter profiles. Often, due to the different physical structures of each of these regions, quite different mathematical models might be most appropriate for describing them in the given context.
Since the image represents physical parameters, it can be tested by physical inspection. Here, the physical parameters typically appear in partial differential equations (PDEs) or in integral equations (IEs) as space-dependent coefficients, and various probing fields are created for measuring the response of the image to these inputs. Due to physical restrictions, these measurements are typically only possible at few discrete locations, often situated at the boundary of the domain Ω, but sometimes also at a small number of points inside Ω. If the underlying PDE is time dependent, then these measurements can be time-dependent functions. The corresponding measured data give information on the spatial distribution of the subdomains and on the corresponding internal model parameters.
Sometimes the physical interpretation of the image is that of a source distribution rather than a parameter distribution. Then, the image itself creates the probing field and needs to be determined from just one set of measured data. Also combinations are possible where some components of the (vector-valued) image describe source distributions and other components describe parameter distributions. Initial conditions or boundary conditions can also often be interpreted as images in this spirit, which need to be determined from indirect data. It is clear that this concept of an image can be generalized even further, which leads to interesting mathematical problems and concepts.
There is often a large variety of additional prior information available for determining the image, whose character depends on the given application. For example, it might be known or assumed that all parameter profiles inside the individual subregions of a domain Ω are constant with known or unknown region-specific values. In this particular case, only the interfaces between the different regions, and possibly the unknown parameter values, need to be reconstructed from the gathered data, which, as a mathematical problem, is much better posed [37, 71] than the task of estimating independent values at each individual pixel or voxel from the same data set without additional prior information on the image. However, in many realistic applications, the image to be found is more complicated, and even the combined available information is not sufficient or adequate for completely and uniquely determining the underlying image. This becomes even worse due to typically noisy or incomplete data, or due to model inaccuracies. Then, it needs to be determined which information on the image is desired and which information can reasonably be expected from the data, taking into account the available additional prior information. Depending on the specific application, different viewpoints are typically taken which yield different strategies for obtaining images which agree (in an application-specific sense) with the given information. We will give some instructive examples further below.
Determining an image (or a set of possible images) from the measured data, in the above-described sense and by taking into account the available additional prior information, is called here imaging or image reconstruction. In practice, images are often represented in a computer and thereby need to be discretized somehow. The most popular discretization model uses 2D pixels or 3D voxels for representing an image, even though alternative models are possible. Often the underlying PDE also needs to be discretized on some grid, which could be done by finite differences, finite volumes, finite elements, and other techniques. The discretization for the image does not necessarily need to be identical to the discretization used for solving the PDE, and sometimes different models are used for discretizing the image and the PDE. However, in these cases, some method needs to be provided to map from one representation to the other. In a level set representation of an image, also the level set functions need to be discretized for being represented in a computer. The above said then holds true also for the discretizations of the level set functions, which could either follow the same model as the PDE and/or a pixel model for the image or follow a different pattern.
The Forward and the Inverse Problem
In this chapter, it is supposed that data 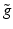 are given in the form
are given in the form
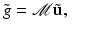
where 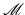 denotes a linear measurement operator, and
denotes a linear measurement operator, and 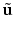 are the physical states created by the sources q for probing the image. It is assumed that a physical model
are the physical states created by the sources q for probing the image. It is assumed that a physical model 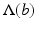 is given, which incorporates the (possibly vector-valued) model parameter b and which is able to (roughly) predict the probing physical states when being plugged into an appropriate numerical simulator, provided the correct sources and physical parameters during the measurement process were known. The forward operator
is given, which incorporates the (possibly vector-valued) model parameter b and which is able to (roughly) predict the probing physical states when being plugged into an appropriate numerical simulator, provided the correct sources and physical parameters during the measurement process were known. The forward operator 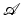 is defined as
is defined as
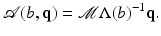
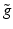 are given in the form
are given in the form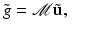
(1)
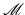 denotes a linear measurement operator, and
denotes a linear measurement operator, and 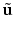 are the physical states created by the sources q for probing the image. It is assumed that a physical model
are the physical states created by the sources q for probing the image. It is assumed that a physical model  is given, which incorporates the (possibly vector-valued) model parameter b and which is able to (roughly) predict the probing physical states when being plugged into an appropriate numerical simulator, provided the correct sources and physical parameters during the measurement process were known. The forward operator
is given, which incorporates the (possibly vector-valued) model parameter b and which is able to (roughly) predict the probing physical states when being plugged into an appropriate numerical simulator, provided the correct sources and physical parameters during the measurement process were known. The forward operator 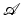 is defined as
is defined as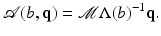
(2)
As mentioned, 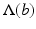 is often described in a form of some partial differential equation (PDE) or, alternatively, an integral equation (IE), and the individual coefficients of the model parameter b appear at one or several places in this model as space-dependent coefficients. In most applications, measurements are taken only at few locations of the domain, for example, at the boundary of the area of interest, from which the physical parameters b or the source q (or both) need to be inferred in the whole domain. It is said that with respect to these unknowns, the measurements are indirect: They are taken not at the locations where the unknowns need to be determined but indirectly by their overall impact on the states (modeled by the underlying PDE or IE) probing the image, which are measured only at few locations. The behavior of the states is modeled by the operator
is often described in a form of some partial differential equation (PDE) or, alternatively, an integral equation (IE), and the individual coefficients of the model parameter b appear at one or several places in this model as space-dependent coefficients. In most applications, measurements are taken only at few locations of the domain, for example, at the boundary of the area of interest, from which the physical parameters b or the source q (or both) need to be inferred in the whole domain. It is said that with respect to these unknowns, the measurements are indirect: They are taken not at the locations where the unknowns need to be determined but indirectly by their overall impact on the states (modeled by the underlying PDE or IE) probing the image, which are measured only at few locations. The behavior of the states is modeled by the operator 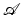 in (2). If in
in (2). If in 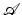 only b (but not q) is unknown, then the problem is an inverse parameter or inverse scattering problem. If in
only b (but not q) is unknown, then the problem is an inverse parameter or inverse scattering problem. If in 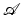 only q (but not b) is unknown, then the problem is an inverse source problem. Given measured data
only q (but not b) is unknown, then the problem is an inverse source problem. Given measured data 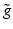 , the “residual operators”
, the “residual operators” 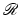 are correspondingly given by
are correspondingly given by
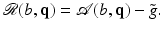
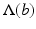 is often described in a form of some partial differential equation (PDE) or, alternatively, an integral equation (IE), and the individual coefficients of the model parameter b appear at one or several places in this model as space-dependent coefficients. In most applications, measurements are taken only at few locations of the domain, for example, at the boundary of the area of interest, from which the physical parameters b or the source q (or both) need to be inferred in the whole domain. It is said that with respect to these unknowns, the measurements are indirect: They are taken not at the locations where the unknowns need to be determined but indirectly by their overall impact on the states (modeled by the underlying PDE or IE) probing the image, which are measured only at few locations. The behavior of the states is modeled by the operator
is often described in a form of some partial differential equation (PDE) or, alternatively, an integral equation (IE), and the individual coefficients of the model parameter b appear at one or several places in this model as space-dependent coefficients. In most applications, measurements are taken only at few locations of the domain, for example, at the boundary of the area of interest, from which the physical parameters b or the source q (or both) need to be inferred in the whole domain. It is said that with respect to these unknowns, the measurements are indirect: They are taken not at the locations where the unknowns need to be determined but indirectly by their overall impact on the states (modeled by the underlying PDE or IE) probing the image, which are measured only at few locations. The behavior of the states is modeled by the operator 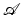 in (2). If in
in (2). If in 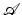 only b (but not q) is unknown, then the problem is an inverse parameter or inverse scattering problem. If in
only b (but not q) is unknown, then the problem is an inverse parameter or inverse scattering problem. If in 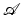 only q (but not b) is unknown, then the problem is an inverse source problem. Given measured data
only q (but not b) is unknown, then the problem is an inverse source problem. Given measured data 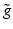 , the “residual operators”
, the “residual operators” 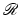 are correspondingly given by
are correspondingly given by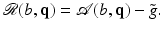
(3)
Given the above definitions, an image is defined here as a mapping
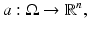 where Ω is a bounded or unbounded region in
where Ω is a bounded or unbounded region in 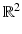 or in
or in 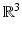 and n is the number of components of the (vector-valued) image. Each component function a k , k = 1, …, n, represents a space-dependent physical characteristic of the domain Ω which can be probed by physical inspection. If it appears as a coefficient of a PDE (or IE), it is denoted a k = b k , and if it appears as a source, it is denoted a k = q k . The exposition given in this chapter mainly focuses on the recovery of parameter distributions a k = b k and addresses several peculiarities related to those cases. However, the main concepts carry over without major changes to inverse source problems and also to some related formulations as, for example, the reconstruction of boundary or initial conditions of PDEs.
and n is the number of components of the (vector-valued) image. Each component function a k , k = 1, …, n, represents a space-dependent physical characteristic of the domain Ω which can be probed by physical inspection. If it appears as a coefficient of a PDE (or IE), it is denoted a k = b k , and if it appears as a source, it is denoted a k = q k . The exposition given in this chapter mainly focuses on the recovery of parameter distributions a k = b k and addresses several peculiarities related to those cases. However, the main concepts carry over without major changes to inverse source problems and also to some related formulations as, for example, the reconstruction of boundary or initial conditions of PDEs.
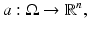
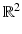 or in
or in 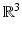 and n is the number of components of the (vector-valued) image. Each component function a k , k = 1, …, n, represents a space-dependent physical characteristic of the domain Ω which can be probed by physical inspection. If it appears as a coefficient of a PDE (or IE), it is denoted a k = b k , and if it appears as a source, it is denoted a k = q k . The exposition given in this chapter mainly focuses on the recovery of parameter distributions a k = b k and addresses several peculiarities related to those cases. However, the main concepts carry over without major changes to inverse source problems and also to some related formulations as, for example, the reconstruction of boundary or initial conditions of PDEs.
and n is the number of components of the (vector-valued) image. Each component function a k , k = 1, …, n, represents a space-dependent physical characteristic of the domain Ω which can be probed by physical inspection. If it appears as a coefficient of a PDE (or IE), it is denoted a k = b k , and if it appears as a source, it is denoted a k = q k . The exposition given in this chapter mainly focuses on the recovery of parameter distributions a k = b k and addresses several peculiarities related to those cases. However, the main concepts carry over without major changes to inverse source problems and also to some related formulations as, for example, the reconstruction of boundary or initial conditions of PDEs.2 Examples and Case Studies
Some illustrative examples and case studies are presented in the following, which will be used further on in this chapter for demonstrating basic ideas and concepts on realistic and practical situations.
Example 1: Microwave Breast Screening
Figure 1 shows two-dimensional images from the application of microwave breast screening. The images of size 160 × 160 pixels have been constructed synthetically based on MRI images of the female breast. Three representative breast structures are displayed in the three images of the left column, where the value at each pixel of the images represents the physical parameter “static relative permittivity.”
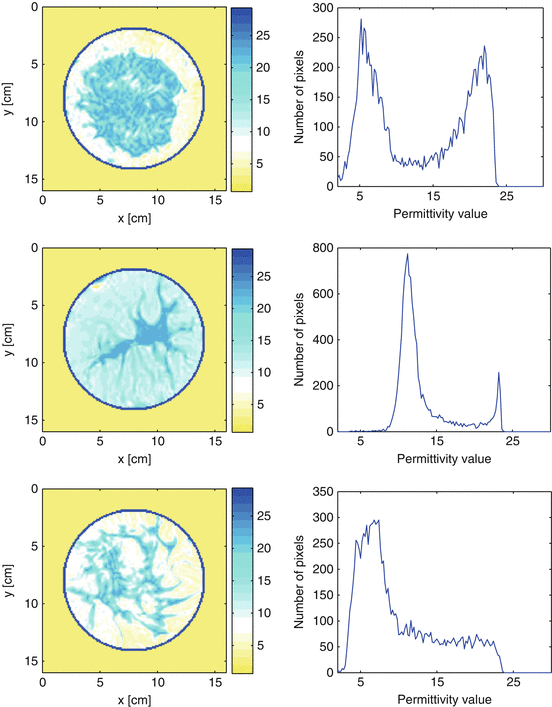

Fig. 1
Three images from microwave breast screening. The three images are synthetically generated from MRI breast models. Left column: two-dimensional maps of the distribution of the static permittivity 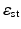 inside the three breast models. Right column: the corresponding histograms of values of
inside the three breast models. Right column: the corresponding histograms of values of 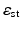 in each map
in each map
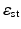 inside the three breast models. Right column: the corresponding histograms of values of
inside the three breast models. Right column: the corresponding histograms of values of 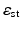 in each map
in each mapA commonly accepted model for breast tissue is to roughly distinguish between skin, fatty tissue and fibroglandular tissue. In the images also a matching liquid is shown in which the breast is immersed. Inside the breast, regions can be identified easily which correspond to fibroglandular tissue (high static relative permittivity values) and fatty tissue (low static relative permittivity values), separated by a more or less complicated interface. On the right column, histograms are shown for the distributions of static relative permittivity values inside the breast. In these histograms, it becomes apparent that values for fatty and fibroglandular tissue are clustered around two typical values, but with a broader range of distribution. However, a clear identification of fatty and fibroglandular tissue cannot be made easily for each pixel of the image based on just these values.
Nevertheless, during a reconstruction, and from anatomical reasoning, it does make sense to assume a model where fatty and fibroglandular tissue occupy some subregions of the breast where a sharp interface exists between these subregions. Finding these subregions provides valuable information for the physician. Furthermore, it might be sufficient for an overall evaluation of the situation to have a smoothly varying profile of tissue parameters reconstructed inside each of these subregions, allowing for the choice of a smoothly varying profile of static relative permittivity values inside each region. In the same spirit, from anatomical reasoning, it makes sense to assume a sharp interface (now of less complicated behavior) separating the skin region from the fatty/fibroglandular tissue on the one side and from the matching liquid on the other side. It might also be reasonable to assume that the skin and the matching liquid have constant static permittivity values, which might be known or not. If a tumor in its early stage of development is sought in this breast model, it will occupy an additional region of small size (and either simple or complicated shape and topology) and might have constant but unknown static relative permittivity value inside this region.
During a reconstruction for breast screening, this set of plausible assumptions provides us with a complex mathematical breast model which incorporates this prior information and might yield an improved and more realistic image for the reconstructed breast (including a better estimate of the tumor characteristics) than a regular pixel-based inversion would be able to provide. This is so because it is assumed that the real breast follows roughly the complicated model constructed above and that this additional information is taken into account in the inversion.
In this application, the underlying PDE is the system of time-harmonic Maxwell’s equations, or its 2D representative (describing so-called TM-waves), a Helmholtz equation. The “static relative permittivity,” as mapped in Fig. 1, represents one parameter entering in the wavenumber of the Debye dispersion model. The electromagnetic fields are created by specifically developed microwave antennas surrounding the breast, and the data are gathered at different microwave antennas also located around the breast. For more details, see [52].
Example 2: History Matching in Petroleum Engineering
Figure 2 shows a synthetically created 2D image of a hydrocarbon reservoir during the production process. Circles indicate injection wells, and crosses indicate production wells. The physical parameter displayed in the image is the permeability, which affects fluid flow in the reservoir. Physically, two lithofacies can be distinguished in this image, namely, sandstone and shaly sandstone (further on simply called “shale”). The sandstone region has permeability values roughly in the range 150–500 mDarcy, whereas shale has permeability values more in the range 900–1,300 mDarcy. In petroleum engineering applications, the parameters inside a given lithofacie sometimes follow an overall linear trend, which is the case here inside the sandstone region. This information is often available from geological evaluation of the terrain. As a rough approximation, inside this region, the permeability distribution can be modeled mathematically as a smooth perturbation of a bilinear model. Inside the shale region, no trend is observed or expected, and therefore the permeability distribution is described as a smooth perturbation of a constant distribution (i.e., an overall smoothly varying profile).
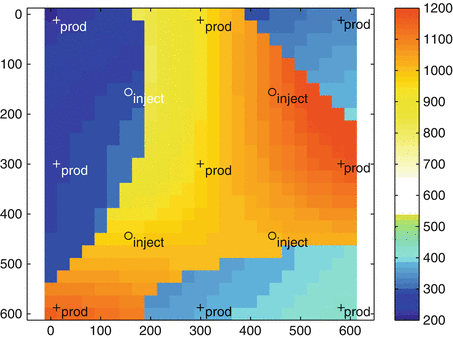

Fig. 2
An image from reservoir engineering. Shown is the permeability distribution of a fluid flow model in a reservoir which consists of a sandstone lithofacie (values in the range of 150–500 mDarcy) and a shaly sandstone lithofacie (values in the range of 900–1,300 mDarcy), separated by a sharp interface. The sandstone region shows an overall linear trend in the permeability distribution, whereas the shaly sandstone region does not show any clear trend
During a reconstruction, a possible model would be to reconstruct a reservoir image from production data which consists of three different quantities: (1) the interface between the sandstone and shale lithofacies, (2) the smooth perturbation of the constant profile inside the shale region, and (3) the overall trend (i.e., the bilinear profile) inside the sandstone region, assuming that inside this sandstone region the smooth perturbation is small compared to this dominant overall trend. In this application, the PDE is a system of equations modeling two-phase or three-phase fluid flow in a porous medium, of which the relative permeability is one model parameter.
The “fields” (in a slightly generalized sense) are represented in this application by pressure values and water/oil saturation values at each point inside the reservoir during production and are generated by injecting (under high pressure) water in the injection wells and extracting (imposing lower pressure) water and oil from the production wells. The data are the injection and production rates of water and oil, respectively, and sometimes pressure values measured at injection and production wells over production time. For more details, see [35].
Example 3: Crack Detection
Figure 3 shows an image of a disconnected crack embedded in a homogeneous material. The cracks are represented in this simplified model as very thin regions of fixed thickness. The physical parameter represented by the image is the conductivity distribution in the domain. Only two values can be assumed by this conductivity, one inside the thin region (crack) and another one in the background. The background value is typically known, and the value inside the crack might either be approximately known or it might be an unknown of the inverse problem. The same holds true for the thickness of the crack, which is assumed constant along the cracks, even though the correct thickness (the constant) might become an unknown of the inverse problem as well. Here insulating cracks are considered, where the conductivity is significantly lower than in the background. The probing fields inside the domain are the electrostatic potentials which are produced by applying voltages at various locations along the boundary of the domain, and the data are the corresponding currents across the boundary at discrete positions.
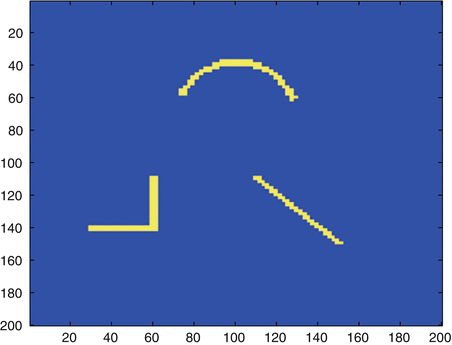

Fig. 3
An image from the application of crack detection. Three disconnected crack components are embedded in a homogeneous background medium and need to be reconstructed from electrostatic measurements at the region boundary. In the considered case of insulating cracks, these components are modeled as thin shapes of fixed thickness with a conductivity value much lower than the background conductivity
This model can be considered as a special case of a binary medium where volumetric inclusions are embedded in a homogeneous background. However, the fact that these structures are very thin with fixed thickness requires some special treatment during the shape evolution, which will be commented on further below. In this application, the underlying PDE is a second-order elliptic equation modeling the distribution of electric potentials in the domain for a set of given applied voltage patterns. For more details, see [4].
3 Level Set Representation of Images with Interfaces
A complex image in the above sense needs a convenient mathematical representation in order to be dealt with in a computational and mathematical framework. In this section, several different approaches are listed which have been proposed in the literature for describing images with interfaces by a level set technique. First, the most basic representation is given, which only considers binary media. Afterwards, various representations are described which represent more complicated situations.
The Basic Level Set Formulation for Binary Media
In the shape inverse problem in its simplest form, the parameter distribution is described by
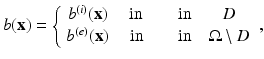
where 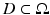 is a subregion of Ω and where usually discontinuities in the parameters b occur at the interface ∂ D. In the basic level set representation for the shape D, a (sufficiently smooth, i.e., Lipschitz continuous) level set function
is a subregion of Ω and where usually discontinuities in the parameters b occur at the interface ∂ D. In the basic level set representation for the shape D, a (sufficiently smooth, i.e., Lipschitz continuous) level set function 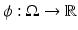 is introduced and the shape D is described by
is introduced and the shape D is described by
![$$\displaystyle{ \left \{\begin{array}{c@{\quad \mbox {for all}\quad }l} \phi ({\mathbf{x}}) \leq 0\quad \mbox{ for all}\quad &{\mathbf{x}} \in D,\\ \phi ({\mathbf{x}} ) > 0\quad \mbox{ for all} \quad &{\mathbf{x}} \in \Omega \setminus D. \end{array} \right. }$$” src=”/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ5.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(5)</DIV></DIV></DIV><br />
<DIV class=Para>In other words, the parameter function <SPAN class=EmphasisTypeItalic>b</SPAN> has the form<br />
<DIV id=Equ6 class=Equation><br />
<DIV class=EquationContent><br />
<DIV class=MediaObject><IMG alt=]() 0. \end{array} \right. }$$” src=”/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ6.gif”>
0. \end{array} \right. }$$” src=”/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ6.gif”>
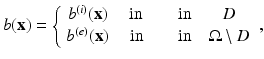
(4)
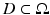 is a subregion of Ω and where usually discontinuities in the parameters b occur at the interface ∂ D. In the basic level set representation for the shape D, a (sufficiently smooth, i.e., Lipschitz continuous) level set function
is a subregion of Ω and where usually discontinuities in the parameters b occur at the interface ∂ D. In the basic level set representation for the shape D, a (sufficiently smooth, i.e., Lipschitz continuous) level set function 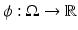 is introduced and the shape D is described by
is introduced and the shape D is described by(6)
Certainly, a unique representation of the image is possible by just knowing those points where ϕ(x) has a change of sign (the so-called zero level set) and additionally knowing the two interior profiles b (i)(x) and b (e)(x) inside those areas of Ω where they are active (which are D and 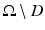 , respectively). Often, however, it is more convenient to assume that these functions are defined on larger sets which include the minimal sets mentioned above. In this chapter, it is assumed that all functions are defined on the entire domain Ω, by employing any convenient extensions from the abovementioned sets to the rest of Ω. Again, it is clear that the above extensions are not unique and that many possible representations can then be found for a given image. Which one to choose depends on details of the algorithm for constructing the image, on the available prior information, and possibly on other criteria (Fig. 4).
, respectively). Often, however, it is more convenient to assume that these functions are defined on larger sets which include the minimal sets mentioned above. In this chapter, it is assumed that all functions are defined on the entire domain Ω, by employing any convenient extensions from the abovementioned sets to the rest of Ω. Again, it is clear that the above extensions are not unique and that many possible representations can then be found for a given image. Which one to choose depends on details of the algorithm for constructing the image, on the available prior information, and possibly on other criteria (Fig. 4).
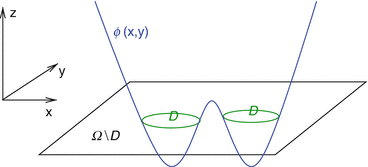
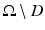 , respectively). Often, however, it is more convenient to assume that these functions are defined on larger sets which include the minimal sets mentioned above. In this chapter, it is assumed that all functions are defined on the entire domain Ω, by employing any convenient extensions from the abovementioned sets to the rest of Ω. Again, it is clear that the above extensions are not unique and that many possible representations can then be found for a given image. Which one to choose depends on details of the algorithm for constructing the image, on the available prior information, and possibly on other criteria (Fig. 4).
, respectively). Often, however, it is more convenient to assume that these functions are defined on larger sets which include the minimal sets mentioned above. In this chapter, it is assumed that all functions are defined on the entire domain Ω, by employing any convenient extensions from the abovementioned sets to the rest of Ω. Again, it is clear that the above extensions are not unique and that many possible representations can then be found for a given image. Which one to choose depends on details of the algorithm for constructing the image, on the available prior information, and possibly on other criteria (Fig. 4).
Fig. 4
The basic level set representation of a shape D. Those points of the domain where the describing level set function assumes negative values are “inside” the shape D described by the level set function ϕ, while those with positive values are “outside” it. The zero level set where ϕ = 0 represents the shape boundary
For a sufficiently smooth level set function, the boundary of the shape D permits the characterization
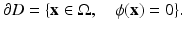
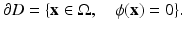
(7)
This representation motivates the name zero level set for the boundary of the shape. In some representations listed further below, however, level set functions are preferred which are discontinuous across those sets where they change sign. Then, the boundary of the different regions can be defined alternatively as
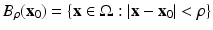 .
.
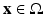 being part of exactly one of the four shapes D ν ; see Fig. 5.
being part of exactly one of the four shapes D ν ; see Fig. 5.
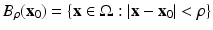 .
. Level Set Formulations for Multivalued and Structured Media
As mentioned already above, in many applications the binary model described in section “The Basic Level Set Formulation for Binary Media” is not sufficient and more complex image models need to be employed. Several means have been discussed in the literature for generalizing the basic model to more complex situations, some of them being listed in the following.
Different Levels of a Single Smooth Level Set Function
A straightforward generalization of the technique described in section “The Basic Level Set Formulation for Binary Media” consists in using, in addition to the level set zero, additional level sets of a given smooth (e.g., Lipschitz continuous) level set function in order to describe different regions of a given domain [99]. For example, define
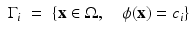
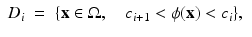
where c i are prespecified values with c i+1 > c i for 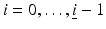 and with c 0 = +∞,
and with c 0 = +∞, 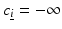 . Then,
. Then,
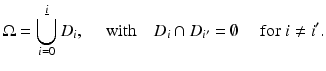
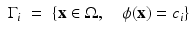
(9)
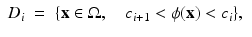
(10)
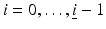 and with c 0 = +∞,
and with c 0 = +∞, 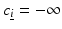 . Then,
. Then,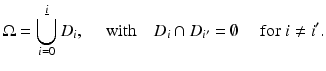
(11)
A level set representation for the image b is then given as a tupel 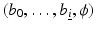 which satisfies
which satisfies
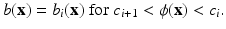
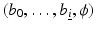 which satisfies
which satisfies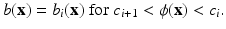
(12)
It is clear that certain topological restrictions are imposed on the distribution of the regions D i by this formulation. In particular, it favors certain nested structures. For more details, see [63].
Piecewise Constant Level Set Function
This model describes piecewise constant multiple phases of a domain by only one level set function and has its origins in the application of image segmentation. A single level set function is used which is only allowed to take a small number of different values, e.g.,
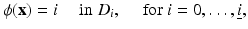
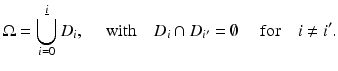
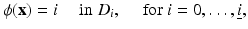
(13)
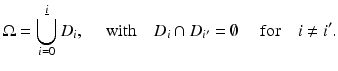
Introducing the set of basis functions γ i
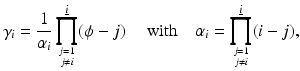
the parameter distribution b(x) is defined as
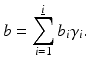
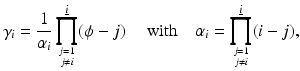
(14)
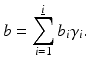
(15)
A level set representation for the image b is then given as a tupel 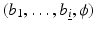 with
with
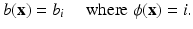
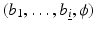 with
with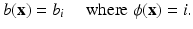
(16)
Vector Level Set
In [99] multiple phases are described by using one individual level set function for each of these phases, i.e.,
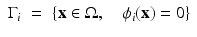
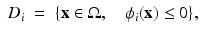
for sufficiently smooth level set functions ϕ i , 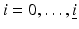 . In this model, the level set representation for the image b is given by a tupel
. In this model, the level set representation for the image b is given by a tupel 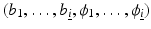 which satisfies
which satisfies
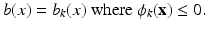
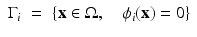
(17)
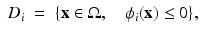
(18)
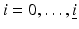 . In this model, the level set representation for the image b is given by a tupel
. In this model, the level set representation for the image b is given by a tupel 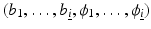 which satisfies
which satisfies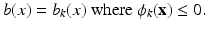
(19)
Care needs to be taken here that different phases do not overlap, which is not automatically incorporated in the model. For more details on how to address this and other related issues, see [99].
Color Level Set
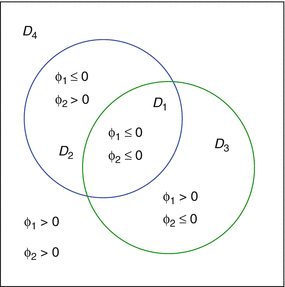
An alternative way of describing different phases by more than one level set functions has been introduced in [95] in the framework of image segmentation and further investigated by [14, 25, 38, 63, 92] in the framework of inverse problems. In this model (which also is known as the Chan–Vese model), up to 2 n different phases can be represented by n different level set functions by distinguishing all possible sign combinations for these functions. For example, a level set representation for an image b containing up to four different phases is given by the tupel (b 1, b 2, b 3, b 4, ϕ 1, ϕ 2) which satisfies
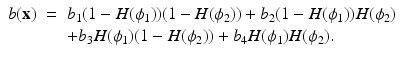
(20)
Also here, the contrast values b ν , ν = 1, …, 4 are allowed to be smoothly varying functions inside each region. The four different regions are then given by
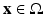 being part of exactly one of the four shapes D ν ; see Fig. 5.
being part of exactly one of the four shapes D ν ; see Fig. 5.
Fig. 5
Color level set representation of multiple shapes. Each region is characterized by a different sign combination of the two describing level set functions
Binary Color Level Set
An alternative technique for using more than one level set function for describing multiple phases, which is, in a certain sense, a combination of the piecewise constant level set model described in section “Piecewise Constant Level Set Function” and the color level set technique described in section “Color Level Set,” has been proposed in [62] for the application of Mumford–Shah image segmentation. For the description of up to four phases by two (now piecewise constant) level set functions ϕ 1 and ϕ 2, in this binary level set model, the two level set functions are required to satisfy
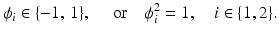
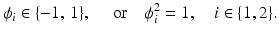
(22)
The parameter function b(x) is given by
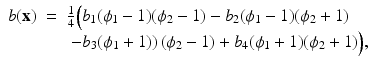
and the four different regions are encoded as
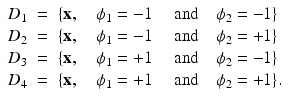
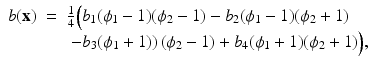
(23)
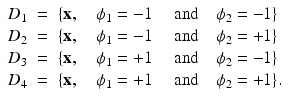
(24)
Level Set Formulations for Specific Applications
Often, for specific applications, it is convenient to develop particular modifications or generalizations of the above-described general approaches for describing multiple regions by taking into account assumptions and prior information which are very specific to the particular application. A few examples are given below.
A Modification of Color Level Set for Tumor Detection
In the application of tumor detection from microwave data for breast screening (see section “Example 1: Microwave Breast Screening”), the following situation needs to be modeled. The breast consists of four possible tissue types, namely, the skin, fibroglandular tissue, fatty tissue, and a possible tumor. Each of these tissue types might have an internal structure, which is (together with the mutual interfaces) one unknown of the inverse problem. In principle, the color level set description using two level set functions for describing four different phases would be sufficient for modeling this situation. However, the reconstruction algorithm as presented in [52] requires some flexibility with handling these four regions separately, which is difficult in this minimal representation of four regions. Therefore, in [52], the following modified version of the general representation of color level sets is proposed for modeling this situation. In this modified version, m different phases (here m = 4) are described by n = m − 1 level set functions in the following form
![$$\displaystyle\begin{array}{rcl} b({\mathbf{x}})& =& b_{1}(1 - H(\phi _{1})) + H(\phi _{1})\Big[b_{2}(1 - H(\phi _{2}))\Big. \\ & & +\Big.H(\phi _{2})\left \{b_{3}(1 - H(\phi _{3})) + b_{4}H(\phi _{3})\right \}\Big] {}\end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ25.gif)
or
![$$\displaystyle\begin{array}{rcl} D_{1}& =& \{{\mathbf{x}},\quad \phi _{1} \leq 0\} \\ D_{2}& =& \{{\mathbf{x}},\quad \phi _{1} > 0\quad \mbox{ and}\quad \phi _{2} \leq 0\} \\ D_{3}& =& \{{\mathbf{x}},\quad \phi _{1} > 0\quad \mbox{ and}\quad \phi _{2} > 0\;\quad \mbox{ and}\quad \phi _{3} \leq 0\} \\ D_{4}& =& \{{\mathbf{x}},\quad \phi _{1} > 0\quad \mbox{ and}\quad \phi _{2} > 0\;\quad \mbox{ and}\quad \phi _{3} > 0\},{}\end{array}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ26.gif”></DIV></DIV><br />
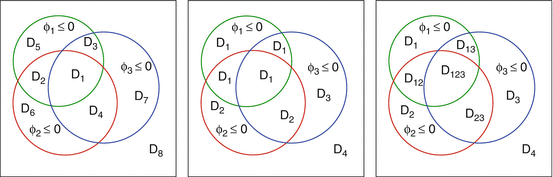
<DIV class=EquationNumber>(26)</DIV></DIV>where <SPAN class=EmphasisTypeItalic>b</SPAN> <SUB>1</SUB>, <SPAN class=EmphasisTypeItalic>b</SPAN> <SUB>2</SUB>, <SPAN class=EmphasisTypeItalic>b</SPAN> <SUB>3</SUB>, and <SPAN class=EmphasisTypeItalic>b</SPAN> <SUB>4</SUB> denote the dielectric parameters of the skin, tumorous, fibroglandular, and fatty tissue, respectively. In (<SPAN class=InternalRef><A href=]() 25), ϕ 1, ϕ 2, and ϕ 3 are the three different level set functions indicating the regions filled with the skin, tumorous, and fibroglandular tissue, respectively, and the contrast values b ν , ν = 1, …, 4 are generally allowed to be smoothly varying functions inside each region. This combination of m − 1 level set functions for describing m different phases has certain advantages with respect to the standard color level set formulation during the reconstruction process, as it is pointed out in [52]. On the other hand, it is obvious that (26) can be considered a special case of the color level set technique (section “Color Level Set”) where the theoretically possible 23 = 8 different values of the color level set description are enforced to fall into m = 4 different groups of characteristic values; see the central image of Fig. 6.
25), ϕ 1, ϕ 2, and ϕ 3 are the three different level set functions indicating the regions filled with the skin, tumorous, and fibroglandular tissue, respectively, and the contrast values b ν , ν = 1, …, 4 are generally allowed to be smoothly varying functions inside each region. This combination of m − 1 level set functions for describing m different phases has certain advantages with respect to the standard color level set formulation during the reconstruction process, as it is pointed out in [52]. On the other hand, it is obvious that (26) can be considered a special case of the color level set technique (section “Color Level Set”) where the theoretically possible 23 = 8 different values of the color level set description are enforced to fall into m = 4 different groups of characteristic values; see the central image of Fig. 6.
Get Clinical Tree app for offline access

![$$\displaystyle\begin{array}{rcl} b({\mathbf{x}})& =& b_{1}(1 - H(\phi _{1})) + H(\phi _{1})\Big[b_{2}(1 - H(\phi _{2}))\Big. \\ & & +\Big.H(\phi _{2})\left \{b_{3}(1 - H(\phi _{3})) + b_{4}H(\phi _{3})\right \}\Big] {}\end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ25.gif)
(25)

Fig. 6
Multiple level set representation for modeling multiphase inverse problems. Left: original color level set technique for describing eight different phases by the different sign combinations of three level set functions. Center: modified color level set technique used in the model for early detection of breast cancer from microwave data. The possible eight regions of the color level set presentation are filled with four different materials in a tailor-made fashion for this application. Right: modified color level set technique for modeling the history matching problem of a water-flooding process in a petroleum reservoir. Also here the eight different regions are filled by a specific combination of materials characteristic for the reconstruction scheme used in this application. Regions with more than one subindex correspond to “characteristic regions” with averaged parameter values
A Modification of Color Level Set for Reservoir Characterization
Another modification of the color level set technique has been used in [35] for the application of history matching in reservoir engineering; see section “Example 2: History Matching in Petroleum Engineering.” Given, as an example, n = 4 level set functions ϕ 1, …, ϕ 4, we define the parameter (permeability) distribution inside the reservoir by
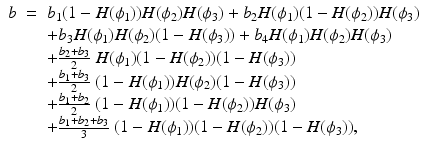
where the permeability values b ν , ν = 1, …, 4 are assumed constant inside each region. The four lithofacies are represented as
![$$\displaystyle\begin{array}{rcl} D_{1}& =& \{{\mathbf{x}},\quad \phi _{1} \leq 0\quad \mbox{ and }\quad \phi _{2}\ > 0\quad \mbox{ and }\quad \phi _{3}\ > 0\} \\ D_{2}& =& \{{\mathbf{x}},\quad \phi _{2} \leq 0\quad \mbox{ and }\quad \phi _{3}\ > 0\quad \mbox{ and }\quad \phi _{1}\ > 0\} \\ D_{3}& =& \{{\mathbf{x}},\quad \phi _{3} \leq 0\quad \mbox{ and }\quad \phi _{1}\ > 0\quad \mbox{ and }\quad \phi _{2}\ > 0\} \\ D_{4}& =& \{{\mathbf{x}},\quad \phi _{1} > 0\quad \mbox{ and }\quad \phi _{2}\ > 0\quad \mbox{ and }\quad \phi _{3}\ > 0\}.{}\end{array}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ28.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(28)</DIV></DIV></DIV><br />
<DIV class=Para>Let in the following <SPAN class=EmphasisTypeItalic>n</SPAN> = 4 be the number of lithofacies. In this model, a point in the reservoir corresponds to the lithofacie <SPAN class=EmphasisTypeItalic>D</SPAN> <SUB><SPAN class=EmphasisTypeItalic>l</SPAN> </SUB>, (<SPAN class=EmphasisTypeItalic>l</SPAN> = 1, <SPAN class=EmphasisTypeItalic>…</SPAN>, <SPAN class=EmphasisTypeItalic>n</SPAN> − 1) if <SPAN class=EmphasisTypeItalic>ϕ</SPAN> <SUB><SPAN class=EmphasisTypeItalic>l</SPAN> </SUB>has negative sign and all the other level set functions have positive sign. In addition, one lithofacie (which here is referred to as the “background” lithofacie with index <SPAN class=EmphasisTypeItalic>l</SPAN> = <SPAN class=EmphasisTypeItalic>n</SPAN>) corresponds to those points where none of the level set functions has a negative sign. Notice that typically this definition does not yield a complete covering of the whole domain Ω by the four (<SPAN class=EmphasisTypeItalic>n</SPAN>) lithofacies; see the right image of Fig. <SPAN class=InternalRef><A href=]() 6. Those regions inside the domain where more than one level set function are negative are recognized as so-called critical regions and are introduced for providing a smooth evolution from the initial guess to the final reconstruction. Inside these critical regions, the permeability assumes values which are calculated as certain averages over values of the neighboring noncritical regions. They are indicated in the right image of Fig. 6 by using multiple subindices indicating which noncritical regions contribute to this averaging procedure. For more details regarding this model, and numerical experiments for the application of reservoir characterization, see [35].
6. Those regions inside the domain where more than one level set function are negative are recognized as so-called critical regions and are introduced for providing a smooth evolution from the initial guess to the final reconstruction. Inside these critical regions, the permeability assumes values which are calculated as certain averages over values of the neighboring noncritical regions. They are indicated in the right image of Fig. 6 by using multiple subindices indicating which noncritical regions contribute to this averaging procedure. For more details regarding this model, and numerical experiments for the application of reservoir characterization, see [35].
(27)
A Modification of the Classical Level Set Technique for Describing Cracks or Thin Shapes
Cracks of finite thickness can be modeled by using two level set functions in a setup which amounts to a modification of the classical level set technique for binary media. For simplicity, assume that a crack or thin region of finite thickness is embedded in a homogeneous background. The classical level set technique described in section “The Basic Level Set Formulation for Binary Media” captures this situation in principle, since the crack can be interpreted as a simple shape (with possibly complicated topology) embedded in a homogeneous background. However, when it comes to shape evolution for such a crack-like structure, it is difficult to maintain a fixed thickness of the thin shape following the classical shape evolution scheme. This is so since the classical shape evolution applies an individually calculated velocity field value in the normal direction at each point of the entire shape boundary, such that the thickness of the thin region will not be maintained. For crack evolution, the deformations of adjacent boundary points need to be coordinated in order to maintain the thickness of the crack during the entire shape evolution; see Fig. 9.
A modified version of the classical level set technique has been proposed in [4, 77] which uses two level set functions for modeling crack propagation and crack reconstruction in this sense. Here, a small neighborhood (narrowband) of the zero level set of the first level set function defines the general outline of the crack, whereas the second level set function selects those parts of this band structure which in fact contribute to the possibly disconnected crack topology.
In more details, given a continuously differentiable level set function ϕ 1 and its zero level set
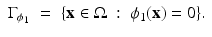
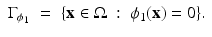
(29)
The normal n to 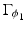 is given by (61) and is pointing into the direction where ϕ(x) ≥ 0. An (connected or disconnected) “ideal” (i.e., of thickness zero) crack with finite length completely contained inside Ω is constructed by introducing a second level set function ϕ 2 which selects one or more parts from the line
is given by (61) and is pointing into the direction where ϕ(x) ≥ 0. An (connected or disconnected) “ideal” (i.e., of thickness zero) crack with finite length completely contained inside Ω is constructed by introducing a second level set function ϕ 2 which selects one or more parts from the line 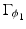 ; see Fig. 7. This second level set function defines the region
; see Fig. 7. This second level set function defines the region
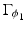 is given by (61) and is pointing into the direction where ϕ(x) ≥ 0. An (connected or disconnected) “ideal” (i.e., of thickness zero) crack with finite length completely contained inside Ω is constructed by introducing a second level set function ϕ 2 which selects one or more parts from the line
is given by (61) and is pointing into the direction where ϕ(x) ≥ 0. An (connected or disconnected) “ideal” (i.e., of thickness zero) crack with finite length completely contained inside Ω is constructed by introducing a second level set function ϕ 2 which selects one or more parts from the line  ; see Fig. 7. This second level set function defines the region
; see Fig. 7. This second level set function defines the region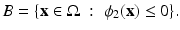
(30)

Fig. 7
Multiple level set representation for modeling a disconnected crack. The zero level set of the first level set function defines the potential outline of the crack, of which the second level set function selects those parts that are actually occupied by the crack. The “ideal” crack has vanishing thickness, whereas the “real” crack modeled by the level set technique has a small finite thickness and is practically obtained by a narrow band technique
The “ideal” crack is then defined as a collection of finite subintervals of 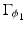
![$$\displaystyle{ S[\phi _{1},\phi _{2}] = \Gamma _{\phi _{1}} \cap B. }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ31.gif)
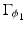
![$$\displaystyle{ S[\phi _{1},\phi _{2}] = \Gamma _{\phi _{1}} \cap B. }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ31.gif)
(31)
An ideal “insulating” crack S (of thickness zero) is then supplemented with a vanishing electrical current condition across this set S[ϕ 1, ϕ 2]. However, in the simplified level set model, not the ideal crack is considered, but cracks of finite thickness 2δ > 0 with known conductivity b i inside the crack and b e outside it. Moreover, in the insulating case, it is assumed that b i ≪ b e . In this model, a small neighborhood of 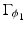 is introduced as
is introduced as
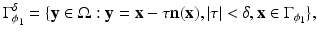
and the above-defined “ideal crack” S is associated now with a “real crack” counterpart
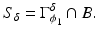
 is introduced as
is introduced as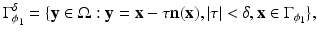
(32)
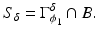
(33)
4 Cost Functionals and Shape Evolution
One important technique for creating images with interfaces satisfying certain criteria is shape evolution, more specifically, interface and profile evolution. The general goal is to start with a set of shapes and profiles as initial guess, and then let both, shapes and profiles, evolve due to some appropriate evolution laws in order to improve the initial guess with increasing artificial evolution time. The focus in the following will be on shape evolution, since evolution laws for interior profiles fairly much follow classical and well-known concepts. Evolution of a shape or an interface can be achieved either by defining a velocity field on the domain Ω which deforms the boundaries of this shape or by defining evolution laws directly for the level set functions representing the shape. Some of these techniques will be presented next.
General Considerations
In many applications, images need to be evaluated for verifying their usefulness or merit for a given situation. This evaluation is usually based on a number of criteria, among them being the ability of the image (in its correct interpretation) to reproduce the physically measured data (its data fitness). Other criteria include the consistence with any additionally available prior knowledge on the given situation or the closeness of the image to a set of reference images. In many cases, some form of merit function (often in terms of a properly defined cost functional) is defined whose value is intended to indicate the usefulness of the image in a given application. However, sometimes this decision is done based on visual inspection only.
In general, during this evaluation process, a family of images is created and the merit of each of these images is assessed. Then, one or more of these images are selected. Let 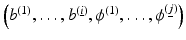 be a level set representation for the class of images to be considered. Then, creating this family of images can be described either in a continuous way by an artificial time evolution
be a level set representation for the class of images to be considered. Then, creating this family of images can be described either in a continuous way by an artificial time evolution
![$$\displaystyle{\left (b^{(1)}(t),\ldots,b^{(\underline{i})}(t),\phi ^{(1)}(t),\ldots,\phi ^{(\underline{j})}(t)\right ),\quad t \in [0,t_{\mbox{ max}}],}$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equc.gif) with an artificial evolution time t or in a discrete way
with an artificial evolution time t or in a discrete way
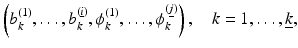 with a counting index k. Usually these images are created in a sequential manner, using evolution laws
with a counting index k. Usually these images are created in a sequential manner, using evolution laws
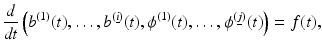 with a multicomponent forcing term f(t) or update formulas
with a multicomponent forcing term f(t) or update formulas
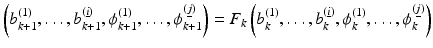 with update operators F k . These evolution laws and update operators can also be defined on ensembles of images, which allows for statistical evaluation of each ensemble during the evaluation process. Any arbitrarily defined evolution law and set of update operators yield a family of images which can be evaluated, but typically those are preferred which point into a descent direction of some predefined cost functional. Some choices of such cost functionals will be discussed in the following.
with update operators F k . These evolution laws and update operators can also be defined on ensembles of images, which allows for statistical evaluation of each ensemble during the evaluation process. Any arbitrarily defined evolution law and set of update operators yield a family of images which can be evaluated, but typically those are preferred which point into a descent direction of some predefined cost functional. Some choices of such cost functionals will be discussed in the following.
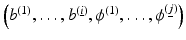 be a level set representation for the class of images to be considered. Then, creating this family of images can be described either in a continuous way by an artificial time evolution
be a level set representation for the class of images to be considered. Then, creating this family of images can be described either in a continuous way by an artificial time evolution![$$\displaystyle{\left (b^{(1)}(t),\ldots,b^{(\underline{i})}(t),\phi ^{(1)}(t),\ldots,\phi ^{(\underline{j})}(t)\right ),\quad t \in [0,t_{\mbox{ max}}],}$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equc.gif)
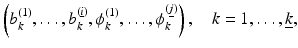
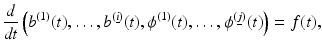
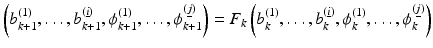
Cost Functionals
In general, a cost functional can consist of various components, typically combined in an additive or multiplicative manner. Popular components for an image model 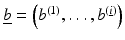 and
and 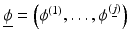 are:
are:
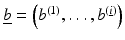 and
and 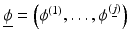 are:
are:1.
Data misfit terms 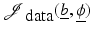
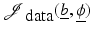
2.
Terms measuring closeness to a prior model inside each subdomain 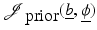
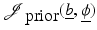
3.
Terms enforcing geometric constraints on the interfaces 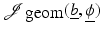
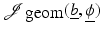
In (1), the by far most popular data misfit term is the least squares misfit cost functional which, in general, is given as an expression of the form
![$$\displaystyle{ \mathcal{J}_{{\mbox{ data}}}(\underline{b},\underline{\phi }) = \frac{1} {2}\left \|\mathcal{A}(\underline{b},\underline{\phi }) -\tilde{ g}\right \|^{2} = \frac{1} {2}\left \|u_{{M}}[\underline{b},\underline{\phi }] -\tilde{ g}\right \|^{2}, }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ36.gif)
where 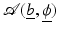 is the forward operator defined in (2) and
is the forward operator defined in (2) and ![$$u_{{M}}[\underline{b},\underline{\phi ]}$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_IEq54.gif) indicates the simulated data at the set of probing locations M for this guess. Other choices can be considered as well; see, for example, [37].
indicates the simulated data at the set of probing locations M for this guess. Other choices can be considered as well; see, for example, [37].
![$$\displaystyle{ \mathcal{J}_{{\mbox{ data}}}(\underline{b},\underline{\phi }) = \frac{1} {2}\left \|\mathcal{A}(\underline{b},\underline{\phi }) -\tilde{ g}\right \|^{2} = \frac{1} {2}\left \|u_{{M}}[\underline{b},\underline{\phi }] -\tilde{ g}\right \|^{2}, }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ36.gif)
(36)
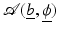 is the forward operator defined in (2) and
is the forward operator defined in (2) and ![$$u_{{M}}[\underline{b},\underline{\phi ]}$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_IEq54.gif) indicates the simulated data at the set of probing locations M for this guess. Other choices can be considered as well; see, for example, [37].
indicates the simulated data at the set of probing locations M for this guess. Other choices can be considered as well; see, for example, [37].(2) corresponds to classical regularization techniques, applied to each subdomain, and is treated in many textbooks, such as [37, 71]. Therefore, it is not discussed in this chapter.
Transformations and Velocity Flows
The first technique discussed here is shape evolution by transformations and velocity flows. This concept has been inspired by applications in continuum mechanics. Given a (possibly bounded) domain 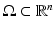 and a shape
and a shape 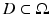 with boundary
with boundary 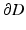 which, as usual, is denoted as
which, as usual, is denoted as 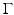 . Let a smooth vector field
. Let a smooth vector field 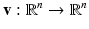 be given with v ⋅ n = 0 on
be given with v ⋅ n = 0 on 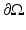 . A family of transformations S t proceeds by
. A family of transformations S t proceeds by
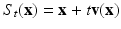
for all 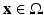 . In short, S t = I + t v where I stands for the identity map. This defines for each point (“particle”) X in the domain, a propagation law prescribed by the ordinary differential equation
. In short, S t = I + t v where I stands for the identity map. This defines for each point (“particle”) X in the domain, a propagation law prescribed by the ordinary differential equation
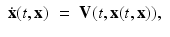
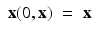
with the specific velocity choice
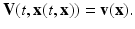
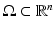 and a shape
and a shape 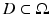 with boundary
with boundary 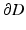 which, as usual, is denoted as
which, as usual, is denoted as 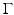 . Let a smooth vector field
. Let a smooth vector field 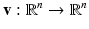 be given with v ⋅ n = 0 on
be given with v ⋅ n = 0 on 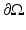 . A family of transformations S t proceeds by
. A family of transformations S t proceeds by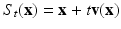
(37)
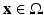 . In short, S t = I + t v where I stands for the identity map. This defines for each point (“particle”) X in the domain, a propagation law prescribed by the ordinary differential equation
. In short, S t = I + t v where I stands for the identity map. This defines for each point (“particle”) X in the domain, a propagation law prescribed by the ordinary differential equation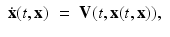
(38)
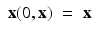
(39)
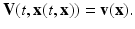
(40)
Physically, it corresponds to the situation where each point X of the domain travels with constant speed along a straight line which is defined by its initial velocity vector v(X). Notice that the definition (40) can with (37) also be written in a slightly more abstract fashion as
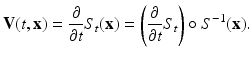
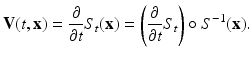
(41)
In fact, it turns out that the ideas in the above example can be considerably generalized from the specific case (40) to quite arbitrary smooth vector fields V(t, x) describing smooth families of transformations T t (X). The generating vector field V(t, x) is often called “velocity field.” It can be done as follows.
Let us given an arbitrary smooth family of transformations T t (X) which maps every point X of the domain to the point x(t, X) = T t (X) at time t. The propagation of the point X over time t is again described by the ordinary differential equations (38) and (39) where the velocity V is defined by
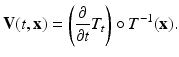
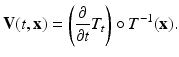
(42)
Now the propagation of points is not restricted anymore to straight lines, but can be quite arbitrary. Vice versa, given a smooth vector field V(t, x), it gives rise to a family of transformations T t (X) via the differential equations (38) and (39) where every point  is mapped by T t (X) to the solution x(t, X) of (38), (39) at time t, i.e., T t (X)(x) = x(t, X). For more details on this duality of transformations and velocity flows, see the well-known monographs [30, 87].
is mapped by T t (X) to the solution x(t, X) of (38), (39) at time t, i.e., T t (X)(x) = x(t, X). For more details on this duality of transformations and velocity flows, see the well-known monographs [30, 87].
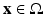 is mapped by T t (X) to the solution x(t, X) of (38), (39) at time t, i.e., T t (X)(x) = x(t, X). For more details on this duality of transformations and velocity flows, see the well-known monographs [30, 87].
is mapped by T t (X) to the solution x(t, X) of (38), (39) at time t, i.e., T t (X)(x) = x(t, X). For more details on this duality of transformations and velocity flows, see the well-known monographs [30, 87].Notice that the numerical treatment of such a velocity flow in the level set framework leads to a Hamilton–Jacobi-type equation. Some remarks regarding this link are given in section “The Level Set Framework for Shape Evolution.”
Eulerian Derivatives of Shape Functionals
Given the framework defined in section “Transformations and Velocity Flows,” the goal is now to define transformations and velocity flows which point into a descent direction for a given cost functional. Some useful concepts on how to obtain such descent directions are discussed here.
Let D = D 0 be a shape embedded in the domain at time t = 0. When the points in the said domain start moving under the propagation laws discussed above, the interior points of the shape, the boundary points, as well as the exterior points will move as well, and therefore the shape will deform. Denote the shape at time t by D t = T t (D 0) where as before T t is the family of transformations which correspond to a given velocity field V(t, x). Assume furthermore that a cost functional 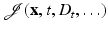 is given which depends (among others) upon the current shape D t . Deformation of shape will entail change of this cost. The so-called shape sensitivity analysis of structural optimization aims at quantifying these changes in the cost due to a given velocity flow (or family of transformations) in order to determine suitable descent flows.
is given which depends (among others) upon the current shape D t . Deformation of shape will entail change of this cost. The so-called shape sensitivity analysis of structural optimization aims at quantifying these changes in the cost due to a given velocity flow (or family of transformations) in order to determine suitable descent flows.
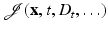 is given which depends (among others) upon the current shape D t . Deformation of shape will entail change of this cost. The so-called shape sensitivity analysis of structural optimization aims at quantifying these changes in the cost due to a given velocity flow (or family of transformations) in order to determine suitable descent flows.
is given which depends (among others) upon the current shape D t . Deformation of shape will entail change of this cost. The so-called shape sensitivity analysis of structural optimization aims at quantifying these changes in the cost due to a given velocity flow (or family of transformations) in order to determine suitable descent flows.Given a vector field V(t, x), the Eulerian derivative of the cost functional 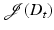 at time t = 0 in the direction V is defined as the limit
at time t = 0 in the direction V is defined as the limit
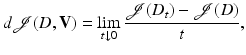
if this limit exists. The functional 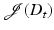 is shape differentiable (or simply differentiable) if the Eulerian derivative
is shape differentiable (or simply differentiable) if the Eulerian derivative 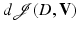 exists for all directions V and furthermore the mapping
exists for all directions V and furthermore the mapping 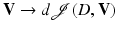 is linear and continuous (in appropriate function spaces). It is shown in [30, 87] that if
is linear and continuous (in appropriate function spaces). It is shown in [30, 87] that if 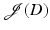 is shape differentiable, there exists a distribution G(D) which is concentrated (supported) on
is shape differentiable, there exists a distribution G(D) which is concentrated (supported) on 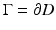 such that
such that
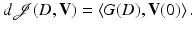
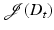 at time t = 0 in the direction V is defined as the limit
at time t = 0 in the direction V is defined as the limit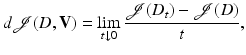
(43)
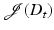 is shape differentiable (or simply differentiable) if the Eulerian derivative
is shape differentiable (or simply differentiable) if the Eulerian derivative 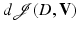 exists for all directions V and furthermore the mapping
exists for all directions V and furthermore the mapping 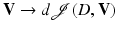 is linear and continuous (in appropriate function spaces). It is shown in [30, 87] that if
is linear and continuous (in appropriate function spaces). It is shown in [30, 87] that if 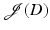 is shape differentiable, there exists a distribution G(D) which is concentrated (supported) on
is shape differentiable, there exists a distribution G(D) which is concentrated (supported) on 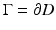 such that
such that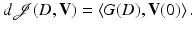
(44)
This distribution G is the shape gradient of 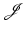 in D, which is a vector distribution. More specifically, let
in D, which is a vector distribution. More specifically, let 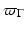 denote the trace (or restriction) operator on the boundary
denote the trace (or restriction) operator on the boundary 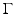 . Then, the Hadamard-Zolésio structure theorem states that (under certain conditions) there exists a scalar distribution g such that the shape gradient G writes in the form
. Then, the Hadamard-Zolésio structure theorem states that (under certain conditions) there exists a scalar distribution g such that the shape gradient G writes in the form 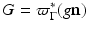 , where
, where 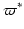 is the transpose of the trace operator at
is the transpose of the trace operator at 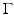 and where n is the normal to
and where n is the normal to 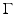 . For more details, see again [30, 87].
. For more details, see again [30, 87].
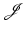 in D, which is a vector distribution. More specifically, let
in D, which is a vector distribution. More specifically, let 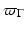 denote the trace (or restriction) operator on the boundary
denote the trace (or restriction) operator on the boundary 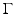 . Then, the Hadamard-Zolésio structure theorem states that (under certain conditions) there exists a scalar distribution g such that the shape gradient G writes in the form
. Then, the Hadamard-Zolésio structure theorem states that (under certain conditions) there exists a scalar distribution g such that the shape gradient G writes in the form 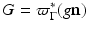 , where
, where 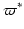 is the transpose of the trace operator at
is the transpose of the trace operator at 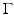 and where n is the normal to
and where n is the normal to 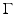 . For more details, see again [30, 87].
. For more details, see again [30, 87]. The Material Derivative Method
A useful concept for calculating Eulerian derivatives for cost functionals is the so-called material and shape derivative of states u. In the application of inverse problems, these states u typically are the solutions of the PDEs (IEs) which model the probing fields and which depend one way or another on the shape D.
Let as before V be a smooth vector field with 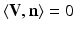 on
on 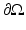 , and let T t (V) denote the corresponding family of transformations. Moreover, let u = u[D t ] be a state function (of some Sobolev space) which depends on the shape
, and let T t (V) denote the corresponding family of transformations. Moreover, let u = u[D t ] be a state function (of some Sobolev space) which depends on the shape 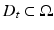 (denote as before D 0 = D). The material derivative
(denote as before D 0 = D). The material derivative ![$$\dot{\mathbf{u}}[D,\mathbf{V}]$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_IEq80.gif) of u in the direction V is defined as
of u in the direction V is defined as
![$$\displaystyle{ \dot{\mathbf{u}}[D,\mathbf{V}] =\lim _{t\downarrow 0}\frac{\mathbf{u}[D_{t}] \circ T_{t}(\mathbf{V}) -\mathbf{u}[D]} {t}, }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ45.gif)
or
 =\lim _{t\downarrow 0}\frac{\mathbf{u}[D_{t}](T_{t}({\mathbf{x}})) -\mathbf{u}[D]({\mathbf{x}})} {t} \quad \mbox{ for}\;{\mathbf{x}} \in \Omega, }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ46.gif)
where the square brackets in the notation indicate the dependence of the states and derivatives on the shape D t and/or on the vector field V. The material derivative corresponds to a Lagrangian point of view describing the evolution of the points in a moving coordinate system, e.g., located in the point x(t, X) = T t (X).
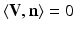 on
on 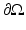 , and let T t (V) denote the corresponding family of transformations. Moreover, let u = u[D t ] be a state function (of some Sobolev space) which depends on the shape
, and let T t (V) denote the corresponding family of transformations. Moreover, let u = u[D t ] be a state function (of some Sobolev space) which depends on the shape 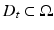 (denote as before D 0 = D). The material derivative
(denote as before D 0 = D). The material derivative ![$$\dot{\mathbf{u}}[D,\mathbf{V}]$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_IEq80.gif) of u in the direction V is defined as
of u in the direction V is defined as![$$\displaystyle{ \dot{\mathbf{u}}[D,\mathbf{V}] =\lim _{t\downarrow 0}\frac{\mathbf{u}[D_{t}] \circ T_{t}(\mathbf{V}) -\mathbf{u}[D]} {t}, }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ45.gif)
(45)
 =\lim _{t\downarrow 0}\frac{\mathbf{u}[D_{t}](T_{t}({\mathbf{x}})) -\mathbf{u}[D]({\mathbf{x}})} {t} \quad \mbox{ for}\;{\mathbf{x}} \in \Omega, }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ46.gif)
(46)
The shape derivative u ′ [D, V] of u in the direction V in contrast corresponds to an Eulerian point of view observing the evolution from a fixed coordinate system, e.g., located in the point X. It is defined as
![$$\displaystyle{ \mathbf{u}^{{\prime}}[D,\mathbf{V}] =\lim _{ t\downarrow 0}\frac{\mathbf{u}[D_{t}] -\mathbf{u}[D]} {t}, }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ47.gif)
or
 =\lim _{ t\downarrow 0}\frac{\mathbf{u}[D_{t}]({\mathbf{x}}) -\mathbf{u}[D]({\mathbf{x}})} {t} \quad \mbox{ for}\;{\mathbf{x}} \in \Omega. }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ48.gif)
![$$\displaystyle{ \mathbf{u}^{{\prime}}[D,\mathbf{V}] =\lim _{ t\downarrow 0}\frac{\mathbf{u}[D_{t}] -\mathbf{u}[D]} {t}, }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ47.gif)
(47)
 =\lim _{ t\downarrow 0}\frac{\mathbf{u}[D_{t}]({\mathbf{x}}) -\mathbf{u}[D]({\mathbf{x}})} {t} \quad \mbox{ for}\;{\mathbf{x}} \in \Omega. }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ48.gif)
(48)
The shape derivative and the material derivative are closely related to each other. It can be shown that
![$$\displaystyle{ \mathbf{u}^{{\prime}}[D,\mathbf{V}] =\dot{ \mathbf{u}}[D,\mathbf{V}] -\nabla (\mathbf{u}[D]) \cdot \mathbf{V}(0) }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ49.gif)
provided that these quantities exist and are well defined. Subtracting ![$$\nabla (\mathbf{u}[D]) \cdot \mathbf{V}(0)$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_IEq81.gif) in (49) from the material derivative makes sure that the shape derivative actually becomes zero in the special case that the states u do not depend on the shape D. The material derivative usually does not vanish in these situations.
in (49) from the material derivative makes sure that the shape derivative actually becomes zero in the special case that the states u do not depend on the shape D. The material derivative usually does not vanish in these situations.
![$$\displaystyle{ \mathbf{u}^{{\prime}}[D,\mathbf{V}] =\dot{ \mathbf{u}}[D,\mathbf{V}] -\nabla (\mathbf{u}[D]) \cdot \mathbf{V}(0) }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ49.gif)
(49)
![$$\nabla (\mathbf{u}[D]) \cdot \mathbf{V}(0)$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_IEq81.gif) in (49) from the material derivative makes sure that the shape derivative actually becomes zero in the special case that the states u do not depend on the shape D. The material derivative usually does not vanish in these situations.
in (49) from the material derivative makes sure that the shape derivative actually becomes zero in the special case that the states u do not depend on the shape D. The material derivative usually does not vanish in these situations. Some Useful Shape Functionals
To become more specific, some useful examples for shape functionals which have been applied to shape inverse problems are provided herein.
1.
Define for a given function ζ the shape integral
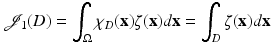
where χ D is the characteristic function for the domain D. Then the Eulerian derivative is given by
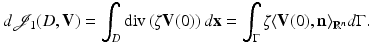
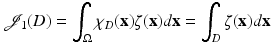
(50)
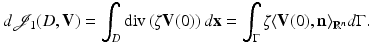
(51)
2.
Consider the shape functional
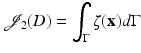
for a sufficiently smooth function ζ defined on Ω such that the traces on 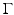 exist and are integrable. The tangential divergence
exist and are integrable. The tangential divergence 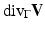 of the vector field V at the boundary
of the vector field V at the boundary 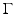 is defined as
is defined as
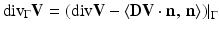
where D V denotes the Jacobian of V. Then,
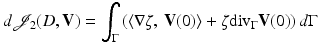
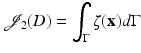
(52)
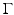 exist and are integrable. The tangential divergence
exist and are integrable. The tangential divergence 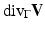 of the vector field V at the boundary
of the vector field V at the boundary 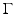 is defined as
is defined as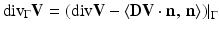
(53)
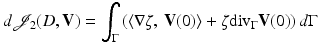
(54)
Be 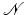 an extension of the normal vector field n on
an extension of the normal vector field n on 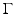 to a local neighborhood of
to a local neighborhood of 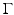 . Then, the mean curvature κ of
. Then, the mean curvature κ of 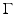 is defined as
is defined as 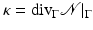 . With that,
. With that, 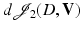 admits the alternative representation
admits the alternative representation
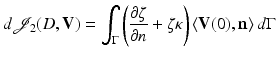
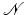 an extension of the normal vector field n on
an extension of the normal vector field n on  to a local neighborhood of
to a local neighborhood of 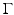 . Then, the mean curvature κ of
. Then, the mean curvature κ of 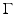 is defined as
is defined as 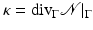 . With that,
. With that, 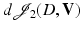 admits the alternative representation
admits the alternative representation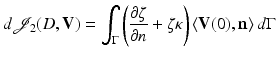
(55)
3.
4.
Consider a cost functional
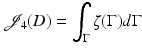
where ζ is only defined at the shape boundary 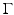 . Then we cannot use the characterization (49) directly, since
. Then we cannot use the characterization (49) directly, since 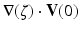 is not well defined. In that case, the shape derivative is defined as
is not well defined. In that case, the shape derivative is defined as
![$$\displaystyle{ \zeta ^{{\prime}}[\Gamma,\mathbf{V}] =\dot{\zeta } [\Gamma,\mathbf{V}] -\nabla _{ \Gamma }(\zeta [\Gamma ]) \cdot \mathbf{V}(0), }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ59.gif)
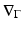 being the gradient along the boundary
being the gradient along the boundary 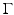 of the shape (chosen such that
of the shape (chosen such that 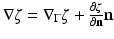 whenever all these quantities are well defined). Then, the Eulerian derivative of the cost functional
whenever all these quantities are well defined). Then, the Eulerian derivative of the cost functional 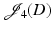 can be characterized as
can be characterized as
![$$\displaystyle{ d\mathcal{J}_{4}(D,\mathbf{V}) =\int _{\Gamma }\zeta ^{{\prime}}[\Gamma,\mathbf{V}]d\Gamma +\int _{ \Gamma }\kappa \zeta \langle \mathbf{V}(0),\mathbf{n}\rangle _{\mathbb{R}^{n}}\,d\Gamma }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ60.gif)
where again κ denotes the mean curvature on 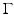 .
.
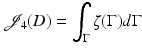
(58)
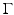 . Then we cannot use the characterization (49) directly, since
. Then we cannot use the characterization (49) directly, since 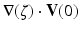 is not well defined. In that case, the shape derivative is defined as
is not well defined. In that case, the shape derivative is defined as![$$\displaystyle{ \zeta ^{{\prime}}[\Gamma,\mathbf{V}] =\dot{\zeta } [\Gamma,\mathbf{V}] -\nabla _{ \Gamma }(\zeta [\Gamma ]) \cdot \mathbf{V}(0), }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ59.gif)
(59)
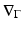 being the gradient along the boundary
being the gradient along the boundary 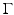 of the shape (chosen such that
of the shape (chosen such that 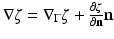 whenever all these quantities are well defined). Then, the Eulerian derivative of the cost functional
whenever all these quantities are well defined). Then, the Eulerian derivative of the cost functional 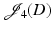 can be characterized as
can be characterized as![$$\displaystyle{ d\mathcal{J}_{4}(D,\mathbf{V}) =\int _{\Gamma }\zeta ^{{\prime}}[\Gamma,\mathbf{V}]d\Gamma +\int _{ \Gamma }\kappa \zeta \langle \mathbf{V}(0),\mathbf{n}\rangle _{\mathbb{R}^{n}}\,d\Gamma }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ60.gif)
(60)
 .
.The Level Set Framework for Shape Evolution
So far, shape evolution has been discussed independently of its representation by a level set technique. Any of the abovementioned shape evolutions can practically be described by employing a level set representation of the shapes.
First, some convenient representations of geometric quantities in the level set framework are listed:
Notice that the right-hand sides of (61




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



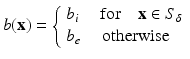
![$$\displaystyle{ \mathcal{J}_{3}(D) =\int _{D}\mathbf{u}[D]d{\mathbf{x}} }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ56.gif)
![$$\displaystyle{ d\mathcal{J}_{3}(D,\mathbf{V}) =\int _{D}\mathbf{u}^{{\prime}}[D,\mathbf{V}]d{\mathbf{x}} +\int _{ \Gamma }\mathbf{u}[D]\langle \mathbf{V}(0),\,\mathbf{n}\rangle _{\mathbb{R}^{n}}\,d\Gamma. }$$](/wp-content/uploads/2016/04/A183156_2_En_11_Chapter_Equ57.gif)