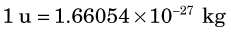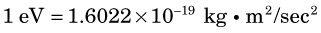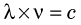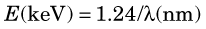a Quantities and Units

1 Types of Quantities and Units

Physical properties and processes are described in terms of quantities such as time and energy. These quantities are measured in units such as seconds and joules. Thus a quantity describes what is measured, whereas a unit describes how much.

Physical quantities are characterized as fundamental or derived. A base quantity is one that “stands alone”; that is, no reference is made to other quantities for its definition. Usually, base quantities and their units are defined with reference to standards kept at national or international laboratories. Time (s or sec), distance (m), and mass (kg) are examples of base quantities. Derived quantities are defined in terms of combinations of base quantities. Energy (kg · m²/sec²) is an example of a derived quantity.

The international scientific community has agreed to adopt so-called System International (SI) units as the standard for scientific communication. This system is based on seven base quantities in metric units, with all other quantities and units derived by appropriate definitions from them. The four quantities of mass, length, time and electrical charge are most relevant to nuclear medicine. The use of specially defined quantities (e.g., “atmospheres” of barometric pressure) is specifically discouraged. It is hoped that this will improve scientific communication, as well as eliminate some of the more irrational units (e.g., feet and pounds). A useful discussion of the SI system, including definitions and values of various units, can be found in reference 1.

SI units or their metric subunits (e.g., centimeters and grams) are the standard for this text; however, in some instances traditional or other non-SI units are given as well (in parentheses). This is done because some traditional units still are used in the day-to-day practice of nuclear medicine (e.g., units of activity and absorbed dose). In other instances, SI units are unreasonably large (or small) for describing the processes of interest and specially defined units are more convenient and widely used. This is particularly true for units of mass and energy, as discussed in the following section.

2 Mass and Energy Units

Events occurring at the atomic level, such as radioactive decay, involve amounts of mass and energy that are very small when described in SI or other conventional units. Therefore they often are described in terms of specially defined units that are more convenient for the atomic scale.

The basic unit of mass is the unified atomic mass unit, abbreviated u. One u is defined as being equal to exactly 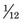the mass of an unbound ¹²C atom * at rest and in its ground state. The conversion from SI mass units to unified atomic mass units is¹

(2-1)

The universal mass unit often is called a Dalton (Da) when expressing the masses of large biomolecules. The units are equivalent (i.e., 1 Da = 1 u). Either unit is convenient for expressing atomic or molecular masses, because a hydrogen atom has a mass of approximately 1 u or 1 Da.

The basic unit of energy is the electron volt (eV ). One eV is defined as the amount of energy acquired by an electron when it is accelerated through an electrical potential of 1 V. Basic multiples are the kiloelectron volt (keV ) (1 keV = 1000 eV ) and the megaelectron volt (MeV ) (1 MeV = 1000 keV = 1,000,000 eV ). The conversion from SI energy units to the electron volt is

(2-2)

Mass m and energy E are related to each other by Einstein’s equation E = mc², in which c is the velocity of light (approximately 3 × 10⁸ m/sec in vacuum). According to this equation, 1 u of mass is equivalent to 931.5 MeV of energy.

Relationships between various units of mass and energy are summarized in Appendix A. Universal mass units and electron volts are very small, yet, as we shall see, they are quite appropriate to the atomic scale.

b Radiation

The term radiation refers to “energy in transit.” In nuclear medicine, we are interested principally in the following two specific forms of radiation:

1 Particulate radiation, consisting of atomic or subatomic particles (electrons, protons, etc.) that carry energy in the form of kinetic energy of mass in motion.

2 Electromagnetic radiation, in which energy is carried by oscillating electrical and magnetic fields traveling through space at the speed of light.

Radioactive decay processes, discussed in Chapter 3, result in the emission of radiation in both of these forms.

The wavelength, λ, and frequency, ν, of the oscillating fields of electromagnetic radiation are related by:

(2-3)

where c is the velocity of light.

Most of the more familiar types of electromagnetic radiation (e.g., visible light and radio waves) exhibit “wavelike” behavior in their interactions with matter (e.g., diffraction patterns and transmission and detection of radio signals). In some cases, however, electromagnetic radiation behaves as discrete “packets” of energy, called photons (also called quanta). This is particularly true for interactions involving individual atoms. Photons have no mass or electrical charge and also travel at the velocity of light. These characteristics distinguish them from the forms of particulate radiation mentioned earlier. The energy of the photon E, in kiloelectron volts, and the wavelength of its associated electromagnetic field λ (in nanometers) are related by

(2-4)

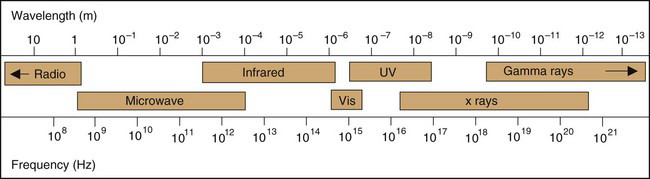
Figure 2-1 illustrates the photon energies for different regions of the electromagnetic spectrum. Note that x rays and γ rays occupy the highest-energy, shortest-wavelength end of the spectrum; x-ray and γ-ray photons have energies in the keV-MeV range, whereas visible light photons, for example, have energies of only a few electron volts. As a consequence of their high energies and short wavelengths, x rays and γ rays interact with matter quite differently from other, more familiar types of electromagnetic radiation. These interactions are discussed in detail in Chapter 6.

FIGURE 2-1 Schematic representation of the different regions of the electromagnetic spectrum. Vis, visible light; UV, ultraviolet light.

c Atoms

1 Composition and Structure

All matter is composed of atoms. An atom is the smallest unit into which a chemical element can be broken down without losing its chemical identity. Atoms combine to form molecules and chemical compounds, which in turn combine to form larger, macroscopic structures.

The existence of atoms was first postulated on philosophical grounds by Ionian scholars in the 5th century bc. The concept was formalized into scientific theory early in the 19th century, owing largely to the work of the chemist, John Dalton, and his contemporaries. The exact structure of atoms was not known, but at that time they were believed to be indivisible. Later in the century (1869), Mendeleev produced the first periodic table, an ordering of the chemical elements according to the weights of their atoms and arrangement in a grid according to their chemical properties. For a time it was believed that completion of the periodic table would represent the final step in understanding the structure of matter.

Events of the late 19th and early 20th centuries, beginning with the discovery of x rays by Roentgen (1895) and radioactivity by Becquerel (1896), revealed that atoms had a substructure of their own. In 1910, Rutherford presented experimental evidence indicating that atoms consisted of a massive, compact, positively charged core, or nucleus, surrounded by a diffuse cloud of relatively light, negatively charged electrons. This model came to be known as the nuclear atom. The number of positive charges in the nucleus is called the atomic number of the nucleus (Z). In the electrically neutral atom, the number of orbital electrons is sufficient to balance exactly the number of positive charges, Z, in the nucleus. The chemical properties of an atom are determined by orbital electrons; therefore the atomic number Z determines the chemical element to which the atom belongs. A listing of chemical elements and their atomic numbers is given in Appendix B.

According to classical theory, orbiting electrons should slowly lose energy and spiral into the nucleus, resulting in atomic “collapse.” This obviously is not what happens. The simple nuclear model therefore needed further refinement. This was provided by Niels Bohr in 1913, who presented a model that has come to be known as the Bohr atom. In the Bohr atom there is a set of stable electron orbits, or “shells,” in which electrons can exist indefinitely without loss of energy. The diameters of these shells are determined by quantum numbers, which can have only integer values (n = 1, 2, 3, …). The innermost shell (n = 1) is called the K shell, the next the L shell (n = 2), followed by the M shell (n = 3), N shell (n = 4), and so forth.

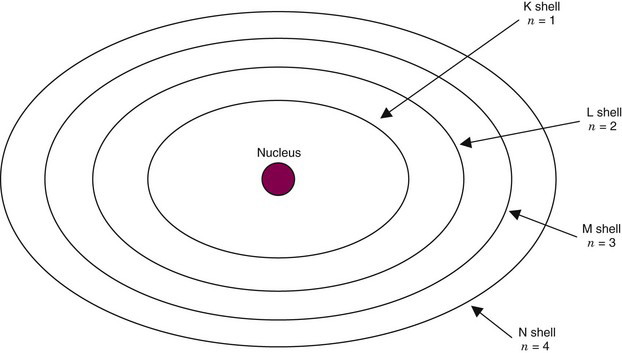
Each shell actually comprises a set of orbits, called substates, which differ slightly from one another. Each shell has 2n − 1 substates, in which n is the quantum number of the shell. Thus the K shell has only one substate; the L shell has three substates, labeled L_I, L_II, L_III; and so forth. Figure 2-2 is a schematic representation of the K, L, M, and N shells of an atom.

FIGURE 2-2 Schematic representation of the Bohr model of the atom; n is the quantum number of the shell. Each shell has multiple substates, as described in the text.

The Bohr model of the atom was further refined with the statement of the Pauli Exclusion Principle in 1925. According to this principle, no two orbital electrons in an atom can move with exactly the same motion. Because of different possible electron “spin” orientations, more than one electron can exist in each substate; however, the number of electrons that can exist in any one shell or its substates is limited. For a shell with quantum number n, the maximum number of electrons allowed is 2n². Thus the K shell (n = 1) is limited to two electrons, the L shell (n = 2) to eight electrons, and so forth.

The Bohr model is actually an over-simplification. According to modern theories, the orbital electrons do not move in precise circular orbits but rather in imprecisely defined “regions of space” around the nucleus, sometimes actually passing through the nucleus; however, the Bohr model is quite adequate for the purposes of this text.

2 Electron Binding Energies and Energy Levels

In the most stable configuration, orbital electrons occupy the innermost shells of an atom, where they are most “tightly bound” to the nucleus. For example, in carbon, which has a total of six electrons, two electrons (the maximum number allowed) occupy the K shell, and the four remaining electrons are found in the L shell. Electrons can be moved to higher shells or completely removed from the atom, but doing so requires an energy input to overcome the forces of attraction that “bind” the electron to the nucleus. The energy may be provided, for example, by a particle or a photon striking the atom.

The energy required to completely remove an electron from a given shell in an atom is called the binding energy of that shell. It is symbolized by the notation K_B for the K shell,* L_B for the L shell (L_IB, L_IIB, L_IIIB for the L shell substates), and so forth. Binding energy is greatest for the innermost shell, that is, K_B > L_B > M_B. Binding energy also increases with the positive charge (atomic number Z) of the nucleus, because a greater positive charge exerts a greater force of attraction on an electron. Therefore binding energies are greatest for the heaviest elements. Values of K-shell binding energies for the elements are listed in Appendix B.