Basic Concepts
Sammy Abid Yacob, DO
Kaushal Mehta, MD
LEARNING OBJECTIVES
1. Understand the principles of radiation and X-ray production.
2. Describe the different forms of photon and charged particle interactions.
3. Define the concepts of exposure, absorbed dose, equivalent dose, and effective dose.
4. Describe the main aspects of image quality.
5. Understand the basic principles of digital imaging.
6. Explain the structure and functions of picture archiving and communication system (PACS).
This chapter reviews physics-related basic concepts in medical imaging and prepares the readers for a more detailed discussions of modality specific topics in the following chapters.
RADIATION AND ATOM
Radiation
Radiation is energy in the form of waves or particles that travels through space or matter. In a broad sense, three types of radiation are used in diagnostic imaging: acoustic radiation, electromagnetic (EM) radiation, and particulate radiation. According to wave-particle duality in quantum mechanics, all three types of radiation have both wave characteristics and particle characteristics. A wave is often described by wavelength, frequency, speed, and amplitude, and a particle by mass, momentum, and energy; any quantum entity, according to wave-particle duality, may be characterized by a combination of these characteristics. Often in medical imaging, a certain type of radiation may demonstrate more pronounced characteristics in one of the two, wave or particle, dependent on the type of object it interacts with. Generally speaking, acoustic radiation and nonionizing EM radiation (like radiofrequency waves used in magnetic resonance imaging [MRI]) are more often treated as waves, and particulate radiation and ionizing radiation (including X-rays and gamma rays) are more often considered as particles.
Acoustic radiation
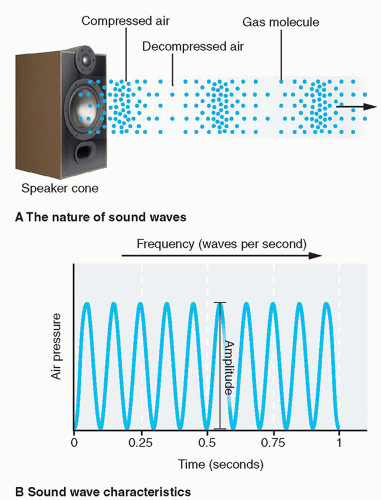
Ultrasound, sound wave at frequencies higher than the upper audible limit of human hearing, is the mainly used acoustic radiation in medical imaging. Other than its higher frequencies, ultrasound is not particularly different from audible sound in physical properties; frequencies of audible sound to humans are typically between 20 and 20 000 Hz (20 kHz), whereas ultrasound imaging devices operate at frequencies from 20 kHz up to a few gigahertz (109 Hz).
Like all other types of waves, the speed (c), wavelength (λ), and frequency (f) of the ultrasound wave are related by the following equation:
c = λ•f
The frequency of ultrasound in imaging is determined by the transducer, which is used to generate the wave. The speed is closely related to the physical properties of the medium in which the ultrasound wave travels. The average speed of ultrasound in soft tissues is about 1540 m/s. If a 5 MHz frequency beam is used for imaging, it can be easily derived that the wavelength of the ultrasound wave is about 0.3 mm (Figure 1.1).
Electromagnetic radiation
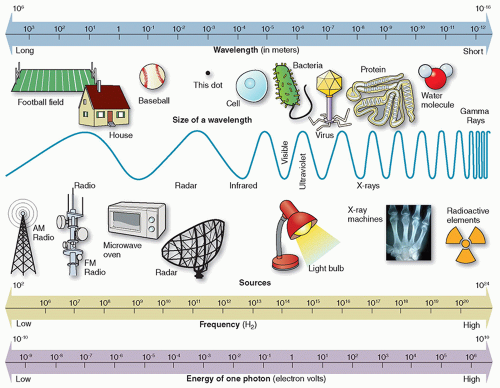
EM radiation is a form of energy that is all around us and takes on many forms. EM radiation encompasses a broad spectrum of energies that comprise the EM spectrum. Categories of EM radiation include radiant heat, radio, TV, microwaves, infrared, visible light, TV light, X-rays, and gamma rays (Figures 1.2 and 1.3).
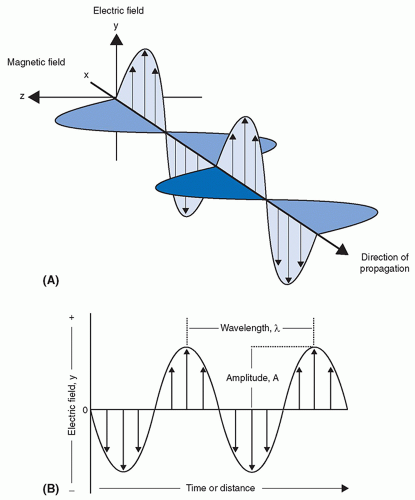
EM radiations have no mass, are unaffected by either electric or magnetic disturbances, and travel at a constant speed in a given medium. The speed of EM radiations is a function of the medium transport characteristics. In a vacuum, EM radiation travels at its maximum speed, the speed of light (2.998 × 108 m/s). EM radiation travels in straight lines; however, this trajectory can be altered by interaction with matter. Interactions can occur either by absorption (removal of radiation) or scattering (change in trajectory).
The types of EM radiation utilized in diagnostic imaging include X-rays, gamma rays, visible light, and radiofrequency EM radiation. X-rays are used in radiography and computed tomographic (CT) imaging. Gamma rays are used in nuclear imaging to image the distribution of radiopharmaceuticals. Visible light, which is produced in detecting X- and gamma rays, is used for the observation and interpretations of images. EM radiation at
radio frequencies is used as the transmission and reception signal for MRI.
radio frequencies is used as the transmission and reception signal for MRI.
Like the ultrasound wave, the EM wave follows the same relation that its speed is equal to the product of the frequency and the wavelength. Because, in air, all EM waves travel at the same speed (˜3.0 × 108 m/s), their frequency varies linearly with the reverse of the wavelength. In the air, wavelengths of X-rays and gamma rays are typically measured in nanometers (nm), where 1 nm = 10-9 m, whereas wavelengths of radio frequency waves used in MRI are typically on the order of meters.
EM radiation can also exhibit particle-like behavior when interacting with matter. It is particularly true for X-rays and gamma rays; they can be viewed as particle-like energy packets, often called photons. Photons are discrete quantities in which EM radiation can be quantified. Photon energy is directly proportional to frequency and inversely proportional to wavelength. The energy of a photon is given by the following equation:
E = hf = hc/λ
where h = Plank’s constant = 6.62 × 10-34 J•s. For X- and gammaray photons, energy (E) is often expressed in keV and wavelength (λ) in nanometers (nm). The energies of photons are commonly expressed in electron volts (eV). One electron volt is the amount of energy gained by an electron when accelerated through an electrical potential difference of one volt in vacuum. Multiples of electron volts (eV) commonly used in medical imaging are the keV (1000 eV) and the MeV (1 000 000 eV).
Ionizing radiation refers to types of radiation where the radiation carries sufficient energy to ionize atoms. In terms of the EM spectrum, radiations of higher frequency, near-UV region of the spectrum, typically carry enough energy per photon to remove bound electrons from atomic shells, thus producing ionized atoms. Ionizing radiation on the EM spectrum includes UV radiation, X-rays, and gamma rays. Nonionizing radiation, or radiations with lower energies, on the EM spectrum includes visible light, infrared, and radio waves.
The threshold energy for ionization depends on the type of matter. Ionization potential is the minimum energy necessary to
remove an electron. For example, the minimum energy necessary to remove an electron (ie, the ionization potential) from water is 12.6 eV.
remove an electron. For example, the minimum energy necessary to remove an electron (ie, the ionization potential) from water is 12.6 eV.
Table 1.1 FUNDAMENTAL PROPERTIES OF PARTICULATE RADIATION | |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||
Particulate radiation
Table 1.1 summarizes the physical properties of particulate radiations associated with medical imaging. They include the following:
Electron
It is the most commonly utilized particulate radiation in diagnostic imaging. An electron has a rest mass of 9.109 × 10-31 kg and a rest energy of 511 keV. Electrons carry a negative charge and exist in atomic orbits. Electrons may also be emitted by the nuclei of some radioactive atoms. In such a case, they are referred to as beta-minus particles (β–), negatrons or “beta particles.”
Positron
Positrons are positively charged electrons. It is the antiparticle or the antimatter particle of electrons.
During radioactive decay, positrons may be emitted from some nuclei.
Proton
Protons are found in the nuclei of all atoms. A proton has a single positive charge and is the nucleus of a hydrogen-1 atom.
Neutrons
Neutrons are uncharged nuclear particles that have a mass slightly greater than a proton. Neutrons are released by nuclear fission and are used for radionuclide production.
Alpha particle
An alpha particle (α2+) consists of two protons and two neutrons; therefore, it carries a net charge of +2 and is identical to the nucleus of a helium atom (4He2+). Certain naturally occurring radioactive materials emit alpha particles, such as uranium, thorium, and radium. In such emissions, the α2+ particle will eventually acquire two electrons from the surrounding medium and become a neutral helium atom (4He).
Mass energy equivalence
According to Einstein’s theory of relativity, mass and energy are interchangeable and the sum of the mass and energy must be conserved. This is true of objects moving at high speeds such as the speeds associated with some nuclear processes, which approach the speed of light. Einstein showed that at these speeds, mass and energy are equivalent according to the expression:
E = mc2
where E represents the energy equivalent to mass (m) at rest and c is the speed of light in a vacuum (2.98 × 108 m/s). For example, the energy equivalent of an electron (mass of 9.109 × 10-31 kg) can be calculated using Einstein’s equation, which turns out to be 0.511 MeV or 511 keV.
A common unit of mass used in atomic and nuclear physics is the atomic mass unit (amu), defined as 1/12th of the mass of an atom of 12C. One amu is equivalent to 931.5 MeV of energy.
Atom
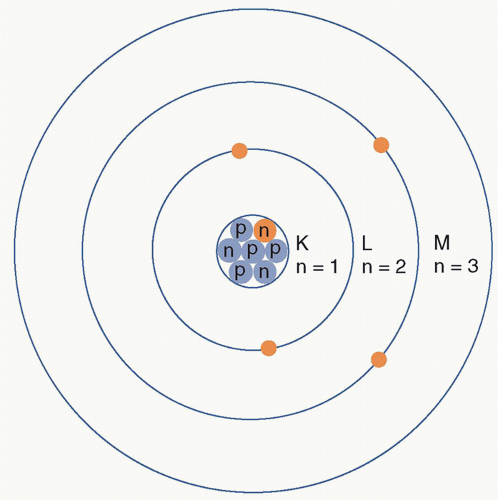
An atom is the smallest constituent unit of matter in which the element’s chemical identity is maintained. The atom is composed of three types of particles: protons, neutrons, and electrons. Protons and neutrons make up the nucleus of an atom, whereas electrons are extranuclear in location.
Protons have a positive charge. Neutrons are electrically neutral. Protons and neutrons are essentially the same mass and together make up the extremely dense atomic nucleus. Electrons are negatively charged and make up the largely unoccupied extranuclear space (Figure 1.4).
Electronic structure
Electron Orbits and Electron Binding Energy
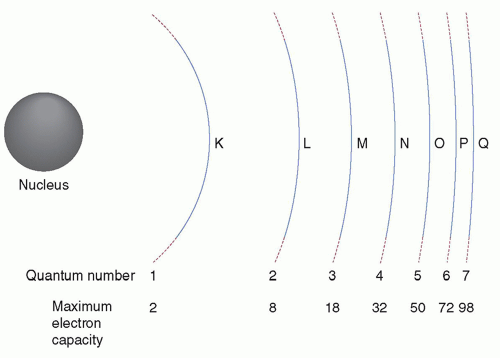
According to the Bohr model of an atom, electrons orbit the dense positively charged nucleus at fixed distances called electron shells. Each electron shell corresponds to a discrete energy state. These electron shells are assigned the letters K, L, M, N, …, with K signifying the innermost shell. Quantum numbers are also assigned, with the quantum number 1 designating the K shell, 2 designating the L shell, and so on.
Each shell can hold a maximum number of electrons, as given by this equation (2n2), where n is the quantum number of the shell. For example, the K shell (n = 1) can only hold two electrons, whereas the L shell (n = 2) can hold 2 × 22 or eight electrons (Figure 1.5).
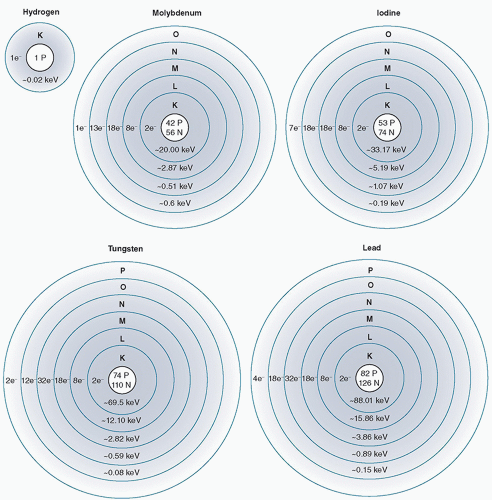
Electrons are held in place by the electrostatic pull of the positively charged nucleus. Electron binding energy is the energy required to remove an electron completely from the atom (Figure 1.6). The binding energy of a particular electron in orbit increases with the number of protons in the nucleus (ie, the atomic number). Therefore, atoms with more positively charged protons have a greater electrostatic pull on the orbiting electrons, which equates to the higher energy required to remove an electron from the atom. Electron binding energies of inner shell electrons are higher than those of more outer-shell electrons because of the decreased electrostatic pull from the positively charged nucleus. The energy required to move an electron from the innermost electron orbit (K shell) to the next orbit (L shell) is the difference between the binding energies of the two orbits. The outermost electron shell of an atom is known as the valence shell. The valence shell determines the chemical properties of the element.
Furthermore, the energy required to move an electron from the innermost electron orbit (K shell) to the next orbit (L shell) is the difference between the binding energies of the two orbits (ie, EbK − EbL) or the transition energy. The K- to L-shell transition energies for hydrogen and tungsten are as follows:
Hydrogen: 13.5 eV − 3.4 eV = 10.1 eV
Tungsten: 69 500 eV − 11 000 eV = 58 500 eV (58.5 keV)
Radiation from Electron Transitions
When an electron is removed from its shell through any interaction, a vacancy is created in that shell. An electron from an outer shell fills this vacancy, subsequently leaving a vacancy that again will be filled by an electron transition from a more distant shell. This series of transitions is called an electron cascade. Each transition releases energy equal to the difference in binding energy between the original and final shells of the electron. The atom may release this energy through emission of either characteristic X-rays or Auger electrons.
Characteristic X-rays
The radiation emitted when an outer-shell electron fills a vacancy in an inner shell of an atom is characteristic of each atom, because the electron binding energies depend on atomic number (Z). Radiation emissions from electron transitions exceeding 100 eV are called characteristic X-rays.
Auger electrons
Characteristic X-rays are not always the product of an electron cascade. Auger electron emission is a competing process that predominates in low Z elements. In Auger electron emission, the energy released is transferred to an orbital electron, typically in the same shell as the cascading electron. The ejected Auger electron possesses kinetic energy equal to the difference between the transition energy and the binding energy of the ejected electron.
The atomic nucleus
Protons and neutrons make up the atomic nucleus and they are collectively known as nucleons. The atomic number (Z) is the number of protons in the nucleus. The mass number (A) is the total number of protons and neutrons (N) within the nucleus, that is, A = N + Z. Note that mass number is different from atomic mass. For example, the mass number of fluorine-19 is 19 (9 protons and 10 neutrons), whereas its atomic mass is 18.9984 amu.
Standard nuclear notation shows the chemical symbol, the mass number, and the atomic number of the isotope. For example, an atom with the chemical symbol X is (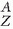 XN). In this notation, Z and N are redundant because the chemical symbol identifies the element and thus the numbers of protons and neutrons. For example, the symbol Tc refers to the technetium atom, which has a Z = 43. Therefore,
XN). In this notation, Z and N are redundant because the chemical symbol identifies the element and thus the numbers of protons and neutrons. For example, the symbol Tc refers to the technetium atom, which has a Z = 43. Therefore, 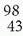 Tc55 is usually simply written as 98Tc or as Tc-98.
Tc55 is usually simply written as 98Tc or as Tc-98.
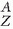 XN). In this notation, Z and N are redundant because the chemical symbol identifies the element and thus the numbers of protons and neutrons. For example, the symbol Tc refers to the technetium atom, which has a Z = 43. Therefore,
XN). In this notation, Z and N are redundant because the chemical symbol identifies the element and thus the numbers of protons and neutrons. For example, the symbol Tc refers to the technetium atom, which has a Z = 43. Therefore, 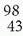 Tc55 is usually simply written as 98Tc or as Tc-98.
Tc55 is usually simply written as 98Tc or as Tc-98.The charge of an atom is indicated by a superscript to the right of the chemical symbol. For example, Al3+ indicates that the aluminum atom has lost three electrons.
Nuclear Forces and Energy Levels
Nuclear forces are the forces that act between the nucleons and bind protons and neutrons (“nucleons”) into atomic nuclei. Nuclear forces are millions of times stronger than chemical binding forces that hold atoms together in molecules. This is why nuclear reactors produce million times more energy per mass unit as compared to chemical fuels like oil or coal.
In the nucleus, there are two main forces that act in opposite directions on particles: the coulombic forces and the exchange forces (aka strong forces). The coulombic forces between protons in the nucleus are repulsive. These forces are countered by the exchange forces which is the exchange of pions (subnuclear particles) among all nucleons. It is the exchange or strong forces that hold the nucleus together, but they only operate over very short nuclear distances (<10-14 m).
Although comparable, the energy levels in the nucleus are often much higher than those in the orbital electron shells. The lowest energy state is called the ground state of an atom. When nuclei
have energy in excess of the ground state, they are said to be in an excited state. Atoms in the excited state have lifetimes with a vast range. Excited states can last from 10-16 s to more than 100 years. Excited states that exist longer than 10-12 s are referred to as metastable or isometric states. These excited nuclei can be denoted by the letter m after the mass number of the atom (ie, Tc-99m).
have energy in excess of the ground state, they are said to be in an excited state. Atoms in the excited state have lifetimes with a vast range. Excited states can last from 10-16 s to more than 100 years. Excited states that exist longer than 10-12 s are referred to as metastable or isometric states. These excited nuclei can be denoted by the letter m after the mass number of the atom (ie, Tc-99m).
Nuclear Binding Energy and Mass Defect
When two subatomic particles approach each other under the influence of this strong nuclear force, their total energy will decrease and the lost energy is emitted in the form of radiation. Therefore, the total energy of the bound particles will be less than the energy of the separated free particles at the expense of the emitted radiation. Atomic binding energy is the energy required to separate an atom into its constituent parts. As such, it is the sum of the electron binding energy and the nuclear binding energy; atomic binding energy is dominated by the much higher nuclear binding energy.
The binding energy can be calculated by subtracting the mass of the atom from the total mass of its constituent protons, neutrons, and electrons; this mass difference is called the mass defect.
For example, an O-16 atom is composed of 8 electrons, 8 protons, and 8 neutrons. Therefore, the total mass of its constituent particles in the unbound state is
Mass of 8 protons + Mass of 8 neutrons + Mass of 8 electrons
= 8 (1.00727 amu) + 8 (1.00866 amu) + 8 (0.00055 amu)
= 16.11591 amu
and the mass of an O-16 atom is 15.99491 amu. Thus, the mass defect of the O-16 atom is
16.11591 amu − 15.99491 amu = 0.12100 amu
Using the mass energy equivalence formula, this mass defect is equal to
(0.121 amu) (931 MeV/amu) = 112.6 MeV
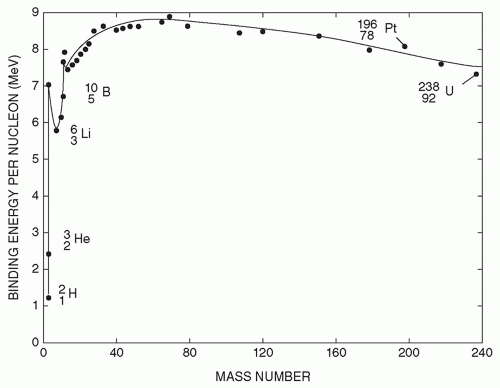
Taking this equation a step further, the binding energy per nucleon can be simply calculated by dividing the total binding energy of the nucleus by the mass number A. Figure 1.7 shows the average binding energy per nucleon as a function of mass number. An extremely important observation to make from this graph is that the curve reaches its maximum near the middle elements and decreases at either end. This predicts that the energy contained in matter can be released. The two processes by which this can occur are called nuclear fission and nuclear fusion.
Nuclides
Nuclides are species of atoms that are characterized by the number of protons, neutrons, and the energy content of the atomic nucleus. Isotopes, isotones, isomers, and isobars are all families of nuclides that share specific properties. Isotopes are nuclides with the same atomic number (Z). Isotones are nuclides with the same number of neutrons (A-Z). Isomers are nuclides with the same atomic and mass numbers but with different energy states. Isobars are nuclides with the same mass number (A).
Nuclear Stability
For a nucleus to be stable there needs to be a certain ratio of neutrons and protons. For nuclides with low atomic number, the ratio of neutrons to protons is approximately 1. However, for nuclides with a high atomic number, the ratio of neutrons to protons is closer to 1.5. In heavier elements, a higher neutron-to-proton ratio is required to offset the coulombic repulsive forces between protons. This ratio can be plotted with Z on the x-axis and N on the y-axis and a nuclide “line of stability” can be plotted, as shown in Figure 1.8.
Radioactivity
Unstable combinations of neutrons and protons do exist. Over time, however, these unstable combinations will transform into nuclei that are stable. Nuclear instability can be classified into two types: neutron excess and neutron deficiency (ie, proton excess).
Unstable nuclei have a surplus of internal energy compared with a stable arrangement of neutrons and protons. The transformation from unstable nuclei to stable nuclei is achieved through the conversion of a neutron to a proton or vice versa, and these events are accompanied by the emission of energy. Nuclides that transform (ie, decay) to more stable nuclei are said to be radioactive and the transformation process is called radioactive decay. The radionuclide at the beginning of a particular decay sequence is called the parent, and the nuclide produced by the decay is called the daughter. Several decays may occur before a stable configuration is achieved. Therefore, the daughter nuclide may be either stable or radioactive.
Unstable nuclei have a surplus of internal energy compared with a stable arrangement of neutrons and protons. The transformation from unstable nuclei to stable nuclei is achieved through the conversion of a neutron to a proton or vice versa, and these events are accompanied by the emission of energy. Nuclides that transform (ie, decay) to more stable nuclei are said to be radioactive and the transformation process is called radioactive decay. The radionuclide at the beginning of a particular decay sequence is called the parent, and the nuclide produced by the decay is called the daughter. Several decays may occur before a stable configuration is achieved. Therefore, the daughter nuclide may be either stable or radioactive.
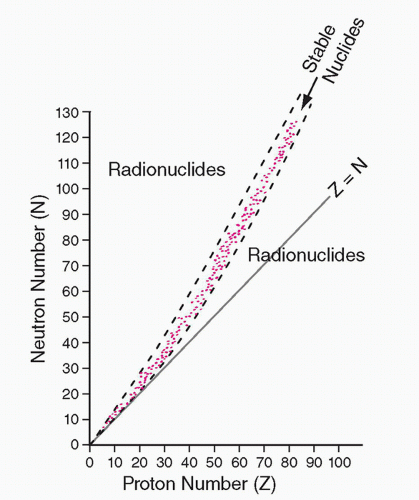 FIG. 1.8 • Plot of the number of neutrons (N) versus the number of protons (Z) for all stable nuclides (points in pink). The line corresponding to equal number of protons and neutron (N = Z) is also shown. When the proton number is low, the ratio N/Z is close to 1 for stable nuclides; when the proton number is high, that ratio approaches approximately 1.5. Radionuclides lie on both sides of the stability curve, with those above for neutron-rich radionuclides and those below for proton-rich ones. Reprinted with permission from Chandra R, Rahmim A. Nuclear Medicine Physics: The Basics. 8th ed. Philadelphia, PA: Wolters Kluwer; 2017.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|