X-Ray Imaging: Fundamentals
Michael Burch, MD
Eric England, MD
Sammy Abid Yacob, DO
Kaushal Mehta, MD
LEARNING OBJECTIVES
1. Name the four major types of interactions for X-ray photons.
2. Define half-value layer (HVL) and describe its relationship with the linear attenuation coefficient (LAC).
3. Explain the beam hardening effect.
4. Name the main components of an X-ray tube and describe their roles in X-ray production.
5. Explain the anode heel effect.
6. Explain the importance of low-voltage rippler for X-ray generators.
7. Explain how automatic exposure control (AEC) works.
X-RAY INTERACTION
Types of interactions
When radiation passes through matter, photons will penetrate, scatter, or be absorbed. X-ray interactions with matter include Rayleigh scattering, Compton scattering, photoelectric absorption, and pair production. Compton scattering and photoelectric absorption are the two most important interactions in diagnostic imaging. Pair production only occurs when photon energy is at least 1.02 MeV, which is not used by medical imaging. Rayleigh scattering, for the photon energies used in diagnostic x-ray imaging applications, is never more than a minor contributor compared to other interaction mechanisms.
Rayleigh scattering
Rayleigh scattering (also called coherent or classical scattering) is an interaction in which the incident photon interacts with an electron of an atom and sets the total atom in the excited state.
The excited atom immediately radiates this energy as an emitting photon of the same energy but in a different direction. As a result, no ionization occurs and no electrons are ejected. The emitted photon undergoes a change in direction without a change in wavelength, and as the X-ray energy decreases, the scattering angle increases (Figure 2.1).
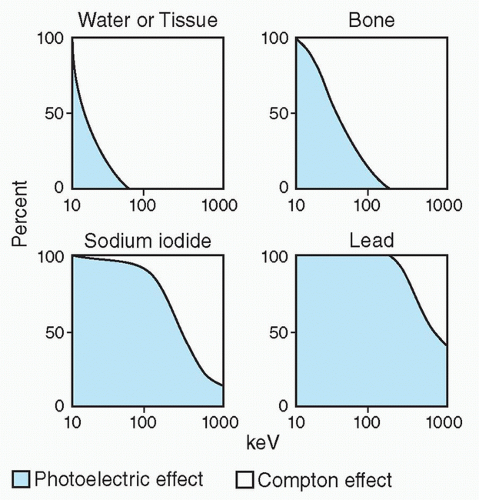
In medical imaging, the image quality is negatively affected by the detection of scattered X-ray. However, in the energy range used in diagnostic imaging the probability of this type of interaction is low. For example, in soft tissues, Rayleigh scattering accounts for less than 5% of X-ray interaction above 70 keV, whereas it accounts for about 12% of interactions at 30 keV.
Compton scattering
In the diagnostic imaging energy range, Compton scattering is the predominate type of interaction of X-ray and gamma-ray photons. In Compton scattering, a photon interacts with an outer shell (valence) electron of an atom. The electron is ejected from the atom and the photon is scattered with some reduction in energy. The energy of the incident photon (E0) is equal to the sum of the energy of the scattered photon (ESC) and the kinetic energy of the ejected electron (Ee−) as
E0 = ESC + Ee−
The binding energy of the electron that was ejected is comparatively small and often ignored (Figure 2.2).
Compton scattering results in the ionization of the atom and the energy of the incident photon is divided between the scattered photon and the ejected electron. The ejected electron will lose its kinetic energy by excitation and ionization of atoms in the surrounding tissues, thereby contributing to the patient’s radiation dose. The Compton scattered photon may travel through the medium without further interactions or may undergo one or more subsequent interactions.
The energy of the incident photon and the angle of the scattered photon can be used to calculate the energy of the scattered photon. This relationship is expressed by the following equation:
ESC = E0/[1 + (E0/511 keV) * (1 − cos θ)]
where ESC is the energy of the scatter photon, E0 is the incident photon energy, and θ is the angle of the scattered photon relative to the incident one. According to the equation, the maximal energy transfer to the Compton electron (the scattered photons goes to its minimum energy at the same time) occurs when the incident photon is scattered back at θ = 180°.
Compared to Rayleigh scattering, the relative probability of a Compton interaction increases as the incident photon energy increases. The probability of a Compton interaction is also dependent on the electron density. With the exception of hydrogen, the total number of electrons per unit mass is fairly constant in tissue; therefore, the probability of Compton scattering per unit mass is essentially independent of Z, and the probability of Compton scattering per unit volume is approximately proportional to the density of the material. Hydrogenous materials have a higher probability of Compton scattering because the absence of neutrons in the hydrogen atom results in increased electron density.
Scattered X-rays provide no useful information for imaging and deteriorate image contrast and quality. Scattered X-rays also provide radiation hazards, particularly in fluoroscopy, in which radiation is scattered from the patient contributing to occupational radiation exposure.
The photoelectric effect
In the photoelectric effect, the incident photon collides with an atom transferring all of its energy to an electron, which is subsequently ejected from the atom. The energy of the ejected electron, called the photoelectron (Ee), is equal to the incident photon energy (E0) minus the binding energy of the orbital electron (Eb) (Figure 2.3).
Ee = E0 − Eb
The probability of photoelectric absorption, by approximation, is considered proportional to Z3/E3, where Z is the atomic number and E is the energy of the incident photon. Therefore, as the atomic number increases, the photoelectric absorption effect becomes more pronounced. This is why barium (Z = 56) and iodine (Z = 53), which have high atomic numbers, are used as contrast agents in X-ray imaging. Also, the probability of photoelectric absorption generally decreases with the increase in photon energy. However, there are sharp discontinuities to be observed at certain photon energies. As the incident photon energy increases to just above the binding energy of the K shell, the absorption of the photon markedly increases. This is known as the K-edge absorption. Every element has one or a few sharp “absorption edges” in which the probability of a photoelectric interaction dramatically increases for photons of energies just above the absorption edge relative to energies just below the edge. For example, an iodine atom which has a K-edge of 33.2 keV is six times more likely to have a photoelectric interaction with a 33.2 keV X-ray photon than with a 33.1 keV photon (Figure 2.4).
The photon energy of an absorption edge is the binding energy of the electrons in a particular shell or subshell. Each different shell or subshell has its own absorption edge. For example, K-edge refers to the absorption edge of the K shell, the closest shell to the nucleus in an atom. The absorption edge corresponding to the same shell typically increases with the atomic number (Z). The absorption edges of the primary elements that comprise soft tissue (H, C, N, and O) are below 1 keV. Iodine (Z = 53) and barium (Z = 56), on the other hand, have K-edges of 33.2 and 37.4 keV, respectively, which provide enhanced X-ray attenuation.
The photoelectric effect plays an important role in soft-tissue imaging, for photon energies below 50 keV. Attenuation differences between tissues with slightly different atomic numbers are amplified by the photoelectric absorption process, which turns into image contrast. This differential absorption is exploited to improve image contrast in various applications. Examples include the selection of X-ray tube target material and fillers in mammography, and the use of phosphors containing rare earth elements (lanthanum and gadolinium) in intensifying screens.
The photoelectric process predominates when lower energy photons interact with high Z materials. Photoelectric absorption serves as the primary mode of interaction of diagnostic X-rays with high Z materials like screen phosphors, radiographic contrast media, and bone. Conversely, Compton scattering predominates at most diagnostic photon energies in materials of lower atomic numbers such as soft tissue and air (Figure 2.5).
Pair production
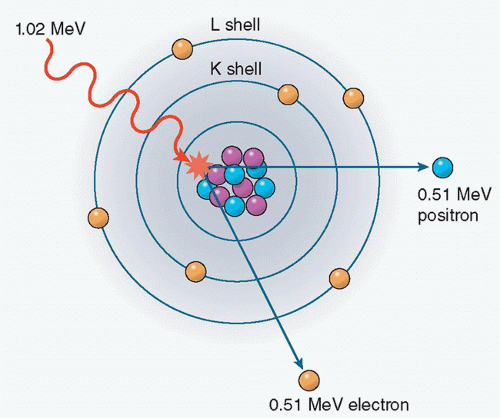
Pair production is not significant in diagnostic X-ray imaging and requires extremely high energies for it to occur. Pair production can only occur when the energies of X-rays exceed 1.02 MeV. In pair production, an X-ray photon interacts with the electric field of the nucleus of an atom and the photon energy is transformed
into an electron-positron pair. Each electron has a rest mass energy equivalent of 0.511 MeV, hence the energy threshold for this reaction to occur is 1.02 MeV. When photon energy is greater than the threshold, the excess is transferred to the electrons as kinetic energy. In turn, the electron and positron lose their kinetic energy via excitation and ionization. A positron may interact with a negatively charged electron as it comes to rest, resulting in the formation of two oppositely directed 0.511 MeV annihilation photons (Figure 2.6).
into an electron-positron pair. Each electron has a rest mass energy equivalent of 0.511 MeV, hence the energy threshold for this reaction to occur is 1.02 MeV. When photon energy is greater than the threshold, the excess is transferred to the electrons as kinetic energy. In turn, the electron and positron lose their kinetic energy via excitation and ionization. A positron may interact with a negatively charged electron as it comes to rest, resulting in the formation of two oppositely directed 0.511 MeV annihilation photons (Figure 2.6).
X-ray attenuation
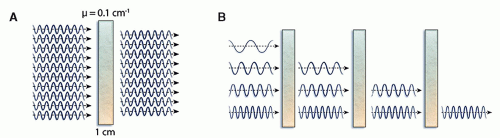
Attenuation is the removal of photons from a beam of X-rays as it passes through matter because of the various types of interactions that may occur (Figure 2.7).
Linear attenuation coefficient
LAC (µ) is the reduction in radiation intensity per unit length. In other words, it is the fraction of photons removed from a monoenergetic beam of X-rays per unit thickness of material. LAC is often expressed in units of inverse centimeters (cm-1). The exponential relationship between the number of incident photons (N0) and those that are transmitted (N) through a thickness x without interaction can be expressed by the following equation:
N = N0e-µx
The LAC is the sum of the individual LACs for each type of interaction:
µ = µRayleigh + µphotoelectric + µCompton scatter + µpair production
In the diagnostic energy range (30-100 keV), the LAC decreases with increasing energy except at absorption edges or the “k-edge”). The LAC for soft tissue ranges from approximately 0.35 to 0.16 cm-1 for photon energies ranging from 30 to 100 keV.
The density of the material also affects the probability of an interaction to occur. For a given thickness of material, the probability of interaction will depend on the number of atoms the X- or gamma rays encounter. Photons will encounter more atoms per unit distance through materials with higher densities.
Half-value layer
The HVL quantifies the tissue penetrability of X-ray photons. It is defined as the thickness of material required to attenuate the intensity of an X-ray beam to half (50%) of its original value. It is important to understand the relationship between the LAC and the HVL. The HVL can be easily calculated from the LAC (µ), and vice versa by the following equation:
HVL = 0.693/µ
HVL is a function of photon energy and attenuating material, and it increases with increasing photon energy and decreases with increasing atomic number of the material.
Effective energy
In radiology, X-ray beams are typically composed of a spectrum of energies; they are often referred to as poly-energetic beams. The HVL, which is usually measured in millimeters of aluminum (mm Al) in diagnostic radiology, can be converted to a quantity called the effective energy. The effective energy of a poly-energetic X-ray beam is essentially an estimate of the penetrating power of the X-ray beam (as if it were a monoenergetic beam).
Beam hardening
In poly-energetic X-ray beams, the lower energy photons will be preferentially removed from the beam as they pass through matter. Beam hardening refers to the shift of the X-ray spectrum towards higher effective energies as the beam transverses matter (Figure 2.8).
Beam hardening may have implications on image quality. Using computed tomography (CT) as an example, the beam hardening effect, if unaccounted for, is known to cause nonuniformity in the reconstructed images of a homogeneous object. To reduce the beam hardening effect, one may insert additional filters in the X-ray beam before it passes through the image object. The added filter not only narrows the X-ray energy spectrum, resulting in less pronounced beam hardening effect, but also removes a larger amount of lower energy X-rays that make little contribution to the image because of their poor tissue penetration.
X-RAY PRODUCTION
An X-ray beam is produced through the interaction of highly energetic electrons with matter. This conversion of kinetic energy into electromagnetic energy from the deceleration of these highly energetic electrons after interacting with a metal target generates X-rays. This interaction occurs in a highly controlled environment, the X-ray tube. The components of the X-ray tube are optimized in medical imaging for the generation of X-rays to visualize the anatomic structure of interest. The following is to review the important aspects of the creation of X-rays, equipment needed to generate these X-rays, and the important characteristics of the X-ray beam.
Bremsstrahlung radiation
X-ray tubes rely on the conversion of electron kinetic energy into electromagnetic radiation for X-ray production. A simplified understanding of the X-ray production process within an X-ray tube is as follows. An X-ray tube can be viewed as a pair of electrodes, enclosed in a vacuum tube, with the negatively charged cathode as the source of the electrons and the positively charged anode as the target. When a large potential difference (voltage) is applied between two electrodes, electrons are accelerated between these electrodes and attain kinetic energy while traveling from the cathode to the anode. The kinetic energy gained by an accelerated electron is measured in electron volts (eV) and is proportional to the potential difference between the cathode and the anode. For example, the energies of electrons accelerated by a potential difference of 20 and 100 kilovolt peak (kVp) are 20 and 100 keV, respectively.
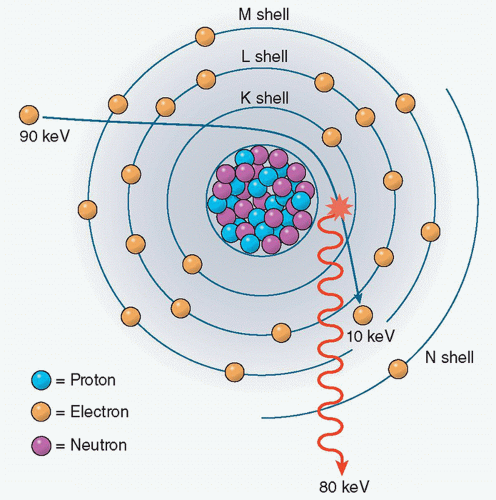
Electrons can be accelerated to different energy levels. When electrons impact the anode, the vast majority of energy is converted to heat through collisional energy exchanges; however, a small fraction of the electrons (about 0.5%) travel close enough to an atomic nucleus within the target that the nucleus slows down and alters the path of the electron. The nucleus is positively charged, and as these electrons near the nucleus, it exerts coulombic attractive forces which decelerate and alter the trajectory of the electron. This process produces an X-ray photon with energy equal to the kinetic energy lost through deceleration. “Bremsstrahlung” is a German word meaning “braking radiation”, which can be understood from the deceleration of the electron. This radiative energy loss is responsible for the majority of the X-rays produced by X-ray tubes (see Figure 2.2).
The distance between the incident electron and the nucleus determines the amount of energy lost by each electron during the bremsstrahlung interaction because the coulombic force of attraction increases with the inverse square of the interaction distance. The coulombic attraction is weak at relatively long distances from the nucleus, and these interactions produce low-energy X-rays. Conversely, for encounters that occur closer to the nucleus, the coulombic forces acting on the electron are greater, the change in the electron’s speed and trajectory are more profound, and the X-rays produced have higher energy. Rarely will the electron collide with the nucleus and lose all of its energy. When this occurs, the maximum X-ray energy is produced (equal to Emax) (Figure 2.9).
The probability of a low-energy interaction is greater than that of a high-energy interaction because on an atomic scale, the atom is mainly empty space and the volume occupied by the atomic nucleus is very small. In fact, the nucleus accounts for about 1/100 000th of the total volume of the atom. As a result, lower X-ray energies are produced in greater numbers, and the quantity of higher energy X-rays decreases with energy up to and including the maximum energy of the incident electrons.
Because the bremsstrahlung process depends on the positive charge of protons in the nucleus, anode elements with a greater atomic number (and thus more protons) are more likely to produce bremsstrahlung radiation. The probability of this interaction occurring for a particular atom is proportional to Z2. Tungsten serves as the anode material for most medical imaging, in part due to its high atomic number (Z = 74) and high melting point.
For completeness sake, it should be noted that particles other than electrons (such as protons and alpha particles) can produce
bremsstrahlung radiation; however, the amount of energy emitted varies inversely with the square of the mass of the incident particle. Because protons and alpha particles are orders of magnitude more massive than are electrons, they produce less than one-millionth the amount of bremsstrahlung radiation as do electrons of the same energy.
bremsstrahlung radiation; however, the amount of energy emitted varies inversely with the square of the mass of the incident particle. Because protons and alpha particles are orders of magnitude more massive than are electrons, they produce less than one-millionth the amount of bremsstrahlung radiation as do electrons of the same energy.
Bremsstrahlung spectrum
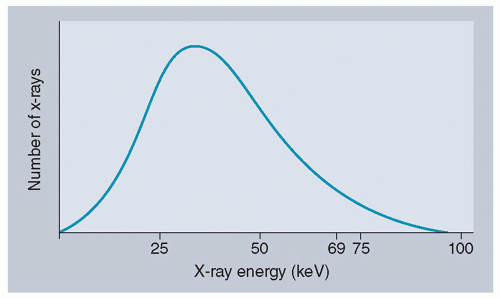
A bremsstrahlung spectrum illustrates the distribution of all X-ray photons produced as a function of energy. The unfiltered bremsstrahlung spectrum demonstrates a linearly decreasing relationship between the number and the energy of the X-rays produced, with the maximum X-ray energy determined by the voltage (kVp) applied across the X-ray tube.
Photons at the lower end of the bremsstrahlung spectrum are of little value in diagnostic imaging and are removed by filtration. This process involves passing the photons through a thin layer of material that preferentially attenuates lower energy X-rays (filtration is discussed in detail later in this chapter). After filtration, a typical bremsstrahlung spectrum shows a distribution with minimal X-rays below 10 keV (Figure 2.10). The average X-ray energy in the filtered spectrum is typically about one-half of the highest X-ray energy (Emax), and the peak of the curve is approximately one-third of Emax. For example, a filtered spectrum with Emax of 120 keV will generally have a peak around 40 keV.
Bremsstrahlung production efficiency
The most important factors affecting X-ray production efficiency are the atomic number of the target material and the kinetic energy of the incident electrons (determined by the voltage potential of the X-ray tube). The ratio of radiative energy loss caused by bremsstrahlung production to collisional (excitation and ionization) energy loss can be approximated with the following equation:
Radiative energy loss/Collisional energy loss = Ek × Z/820 000
where Ek is the kinetic energy of the incident electrons in keV and Z is the atomic number of the target material.
For energy levels used in diagnostic medical imaging, the vast majority of incident energy is converted to heat. As an example, for 100 keV electrons colliding with tungsten (Z = 74), the approximate ratio of radiative to collisional losses is (100 × 74)/820 000 = 0.009 or 0.9%. Therefore, about 99.1% of the incident energy will be released as heat.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree