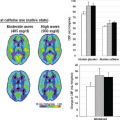
Basic Principles of Arterial Spin Labeling: Continuous versus Pulsed Arterial Spin Labeling
Yufen Chen
John A. Detre
Arterial spin labeling (ASL) is a magnetic resonance imaging (MRI) technique that uses radiofrequency (RF) pulses to alter the magnetization of inflowing blood spins, which results in a change in tissue magnetization related to perfusion. Because it converts blood into an intrinsic (endogenous) tracer, ASL is entirely noninvasive and is especially well suited for vulnerable populations, such as patients and children. However, the ASL signal change in brain tissue is just on the order of 1% in humans, and the technique also induces many other effects that interfere with the perfusion contrast. All ASL experiments require two conditions: control and tag, which are subtracted to eliminate the unwanted effects and separate the perfusion signal from the much higher background tissue signal. The small signal change also necessitates signal averaging to increase the signal-to-noise ratio (SNR). This restricts the type of image acquisition method that can be paired with the ASL preparation because slow acquisition methods will result in a prohibitively long scan time. A fast imaging readout method is even more critical for human ASL studies because the RF field cannot be maintained throughout the entire scan for safety reasons. This means the ASL signal will start to decay at the rate of T1 of blood as soon as the RF field is turned off. Thus, ASL is typically implemented with fast imaging readout methods, such as echo-planar imaging (EPI) or spiral imaging (see Chapter 16).
Since it was first introduced in 1992,1 many ASL techniques have been developed. Most ASL implementations fall into two broad categories: continuous ASL (CASL), where a continuous stream of altered blood spins is maintained, and pulsed ASL (PASL), where a bolus of altered blood spins is created with a short RF pulse. In fact, both CASL and PASL create a bolus of labeled spins. With CASL, a thin slab is continuously irradiated, so all the blood passing through this slab will be labeled (either inverted or saturated) and then move downstream, while with PASL, a slab of blood is labeled, which then moves along with the blood flow. Regardless of whether one labels a slab at once (PASL) or continuously labels snippets of spins for a given labeling period (CASL), the basic principle of ASL is always the same: (1) create a tag of certain spatial extent; (2) wait some time until the labeled blood reaches the capillaries; and then (3) image.
Implementing ASL on humans requires many modifications to the original technique owing to the slower velocity and lower blood flow. These will be discussed in more detail in the following sections.
Continuous Arterial Spin Labeling
In CASL, a continuous stream of labeled blood spins changes the steady state signal of tissue through exchange of these spins between capillaries and tissue. The continuous labeling can be achieved with either a train of slab-selective saturation pulses1 or low-powered continuous inversion with gradients.2 Because inversion affords twice the amount of perfusion signal compared with saturation, it has become the method of choice for CASL. In most CASL studies, the RF field is applied for 2 to 3 seconds. Because RF amplifiers used in most clinical MRI scanners are not designed to provide truly continuous RF, CASL is usually implemented with long blocks of inversion RF fields broken up by small gaps so the duty cycle is less than 100%.
Did you Know ThatA pseudo-continuous ASL approach that approximates continuous inversion with multiple, low flip angle pulses was introduced to circumvent increased hardware limitations on duty cycle associated with body transmit and receive array systems. For details on pseudo-continuous ASL, see Chapter 17.
Adiabatic Fast Passage
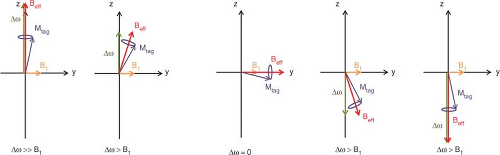
Inversion of blood spins in traditional CASL2 is based on flow-induced or flow-driven adiabatic fast passage, an extension of the traditional adiabatic passage principle that states that, provided the direction of the effective magnetic field (Beff) does not change significantly during the precession period of the spin vector around Beff, the spin vector
ill follow the direction of Beff. Traditional adiabatic conditions are achieved with frequency-modulated RF pulses, but in flow-driven adiabatic fast passage, the varying frequency is achieved with the flowing motion of spins along a magnetic field gradient. Without loss of generality, assume that the RF or B1 field is applied to the y-axis, orthogonal to a magnetic field gradient played out in the direction of the z-axis, and that flowing spins are moving along the gradient direction (z-axis). Static spins at the inversion plane are thus on resonance and will experience a large flip angle, but they will not contribute to the perfusion signal. Spins flowing toward the inversion plane will experience an effective field Beff, which is a combination of the frequency offset (Δω) dependent on the strength of the gradient, the spin’s distance from the inversion plane, and the applied B1. The direction and magnitude of the Beff will be determined by the vector sum of Δω and the applied B1. At locations far away from the inversion plane, Δω will be greater than the applied B1 field amplitude, resulting in a Beff parallel to the z-axis. As the spin moves closer to the inversion plane, the contribution of Δω to Beff decreases, while the contribution of the applied RF field increases, resulting in a Beff in the transverse plane. This process will be reversed as the spin moves away from the inversion plane, resulting in negative Δω contribution until eventually the Beff becomes antiparallel to the main field and net inversion occurs. A schematic of this process is shown in Figure 15.1. Flow-driven inversion will only occur if the flow velocity is high enough such that T2 decay during the applied B1 field is negligible and low enough such that the adiabatic condition is satisfied. These requirements are represented mathematically in the following equation:
ill follow the direction of Beff. Traditional adiabatic conditions are achieved with frequency-modulated RF pulses, but in flow-driven adiabatic fast passage, the varying frequency is achieved with the flowing motion of spins along a magnetic field gradient. Without loss of generality, assume that the RF or B1 field is applied to the y-axis, orthogonal to a magnetic field gradient played out in the direction of the z-axis, and that flowing spins are moving along the gradient direction (z-axis). Static spins at the inversion plane are thus on resonance and will experience a large flip angle, but they will not contribute to the perfusion signal. Spins flowing toward the inversion plane will experience an effective field Beff, which is a combination of the frequency offset (Δω) dependent on the strength of the gradient, the spin’s distance from the inversion plane, and the applied B1. The direction and magnitude of the Beff will be determined by the vector sum of Δω and the applied B1. At locations far away from the inversion plane, Δω will be greater than the applied B1 field amplitude, resulting in a Beff parallel to the z-axis. As the spin moves closer to the inversion plane, the contribution of Δω to Beff decreases, while the contribution of the applied RF field increases, resulting in a Beff in the transverse plane. This process will be reversed as the spin moves away from the inversion plane, resulting in negative Δω contribution until eventually the Beff becomes antiparallel to the main field and net inversion occurs. A schematic of this process is shown in Figure 15.1. Flow-driven inversion will only occur if the flow velocity is high enough such that T2 decay during the applied B1 field is negligible and low enough such that the adiabatic condition is satisfied. These requirements are represented mathematically in the following equation:
where G is the gradient amplitude, ν is flow velocity,
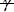is the gyromagnetic ratio, which is 42.56 MHz/T for protons, and
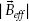is the magnitude of the effective field.
 FIGURE 15.1. Adiabatic fast passage. The flowing spin will precess around effective magnetic field (Beff) and be inverted as it flows through the inversion plane provided the adiabatic condition is satisfied. |
Quantification
Quantification for CASL can be most easily understood by modifying the Bloch equations2 to include the effects of flow (f) on tissue magnetization, Mt:
where Mt0 is the equilibrium magnetization of tissue, T1t the T1 of tissue, Ma is the arterial blood magnetization, and λ is the brain–blood partition coefficient of water. Because all ASL experiments involve a subtraction between control and tag conditions, the above equation for both the control and tag conditions can be combined by defining ΔMt = Mt,control − Mt,tag, ΔMa = Ma,control − Ma,tag, and 1/T1app = 1/T1t + f/λ3:
The difference in arterial magnetization, ΔMa, is dependent on (1) the inversion efficiency α; (2) the equilibrium magnetization of blood Ma0; and (3) T1 relaxation of blood during the time it travels from the inversion plane to the imaging plane, also known as the transit delay or δ:
Eq. 3 is a standard first order linear differential equation of the form
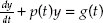. By defining an integration factor
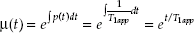multiplying both sides of the quality in Eq. 3 by this factor, and integrating, a solution for ΔMt can be found:
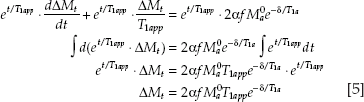
Notice in this equation ΔMt is not time dependent. This result is only true if a sufficiently long labeling duration is used so that steady state is achieved in tissue magnetization. Compared with the equations in the original paper2 on CASL, Eq. 5 also has an additional exponential term involving δ. This is because the original CASL experiment was demonstrated in rats where δ ≪ T1a, so this term has negligible effect on ΔMt. In humans, where δ is much longer, this is a significant source of error that needs to be corrected (as explained later in the chapter).
Did you Know ThatThe term Ma0 is often replaced by Mt0/λ in many ASL papers because of the difficulty in measuring Ma0, which should ideally be extracted from a voxel filled completely with arterial blood. This is not possible at the typical ASL resolution of 3 mm in plane. Calculating Ma0 from Mt0/λ has the added bonus of removing inhomogeneities in coil sensitivity, although this approach has caused some confusion in the field because it implies Ma0 is tissue dependent when in fact it is not.4
In addition to modified Bloch equations, Buxton’s general kinetic model5 can also be used for cerebral blood flow (CBF) quantification in CASL. This model consists of three functions:
Delivery function, c(t): assuming the blood arrives at the tissue via uniform plug flow, c(t) defines a square bolus of width τ arriving at t = δ. Mathematically, c(t) is defined as:
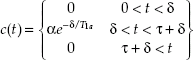
which already reflects the label arrival, label efficiency, and the effect that the label decays with T1a.
Residue function, r(t): describes the exchange of tagged spins between blood and tissue: r(t) = e−ft/λ.
Magnetization relaxation function, m(t): describes the continued relaxation of spins after exchange into tissue: m(t) = e−t/T1t.
These three functions are combined as follows to account for the relationship between ΔMt and f:
where * represents the mathematical convolution operation. The piecewise solution for Eq. 6 is:
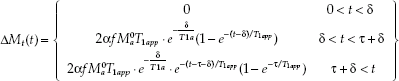
Notice in Buxton’s kinetic model, a finite labeling duration τ is used, and ΔMt is now time dependent. If τ is sufficiently long, so that brain tissue reaches a steady-state signal, Buxton’s equations will reduce to Eq. 5.
Did you Know ThatEqs. 1 through 6 assume single compartment kinetics where there is complete exchange of blood into tissue upon arrival. This model was inherited from positron emission tomography studies, which are on a much longer time scale than the typical ASL experiment. Its validity for ASL has since been challenged. Today, more complicated quantification models involving multiple compartments have been proposed. For details, see Chapter 30.
Measuring Inversion Efficiency
The inversion efficiency, α, is defined as the signal difference of blood between the control and tag conditions, expressed as a percentage of the maximum possible signal difference. It is expressed mathematically as follows:
In a perfect inversion, Ma = −Ma0, the maximum possible signal difference is 2Ma0, yielding α = 1. Practically, α is always less than 1 because of loss of efficiency through processes such as signal relaxation and magnetization transfer effects. Therefore, α should be measured to ensure accuracy of CBF quantification. The most traditional method to measure α is to acquire “control” and “tag” images of the labeled blood vessels downstream of the inversion plane. Typically a flow-compensated gradient-echo sequence is used to minimize flow artifacts. The spatial resolution of these images must be high enough to discern the blood vessels from surrounding tissue with minimal partial volume effects. It is important to remember that MRI only saves magnitude images by default, which leads to signal reversal in the case of inversions; therefore, phase images must also be used to compute the real signal within the blood vessel. With the real signal intensities, Eq. 7 can be used to calculate α.
Alternatively, inversion efficiency can also be obtained from a combination of an ASL experiment and phase-contrast MRI.6 Phase-contrast MRI provides a measure of blood velocity, which when integrated over the cross-sectional area of a major feeding artery, provides the blood flow to the brain for that artery. The sum
of blood flow from all inflowing arteries will provide an estimate of total blood flow to the brain in units of milliliters per second. Division of this value by the total intracranial mass will yield the mean blood flow per unit mass, which is equivalent to the whole brain ASL signal divided by α, thus α can be calculated from a ratio between the total blood flow calculated from phase-contrast MRI and ASL. In order to estimate intracranial mass in vivo, a high-resolution anatomical image can be used to provide a rough estimate of the total intracranial volume, which is then multiplied by an assumed brain density of 1.06 g/mL7 to yield intracranial mass.
of blood flow from all inflowing arteries will provide an estimate of total blood flow to the brain in units of milliliters per second. Division of this value by the total intracranial mass will yield the mean blood flow per unit mass, which is equivalent to the whole brain ASL signal divided by α, thus α can be calculated from a ratio between the total blood flow calculated from phase-contrast MRI and ASL. In order to estimate intracranial mass in vivo, a high-resolution anatomical image can be used to provide a rough estimate of the total intracranial volume, which is then multiplied by an assumed brain density of 1.06 g/mL7 to yield intracranial mass.
Pitfalls and Remedies
Magnetization Transfer Effects
One of the most significant sources of error in CASL is magnetization transfer (MT) effects. The long inversion RF pulse saturates bound protons on macromolecules in both flowing blood and static tissue located off resonance to the inversion plane. Exchange of these bound protons with those on free water leads to loss in inversion efficiency, which is exacerbated at low blood velocities.8 MT also causes up to 60% signal decrease in the imaging slice, which far exceeds the perfusion-related signal change. The most effective remedy for these problems is to use two separate coils for labeling and imaging.9 A small surface coil, with limited spatial extent of B1, can be used to label fast-flowing blood in the neck, thereby reducing the effect of MT on inversion efficiency at the expense of longer transit time. The increased distance between the label location and imaging region and the limited spatial coverage of surface labeling coils also eliminates MT effects in the imaging region. Unfortunately, this method has not been widely used because it requires additional hardware and is highly sensitive to vessel geometry.
 FIGURE 15.2. Diagrams showing the location of the inversion planes for the control and tag conditions in single-slice continuous arterial spin labeling (CASL) and amplitude-modulated (AM-CASL). In AM-CASL, the amplitude modulation during control is equivalent to two adjacent inversion planes, resulting in no net inversion. |
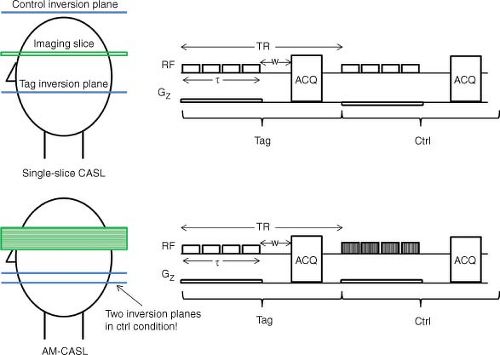
For single-coil CASL, MT can be minimized by applying the same inversion RF to a plane located above (or alternated side of) the imaging slice at the same distance offset as the inversion plane below.2 However, this method requires both inversion planes to be parallel and equidistant from the imaging slice and can only be used for single slice acquisitions, which greatly limits its applications. This shortcoming can be mitigated with amplitude-modulated CASL (AM-CASL),10 where the same inversion RF applied at frequency f0 used in the tag condition is multiplied by a sine wave at frequency f1 in the control condition. This amplitude modulation is equivalent to applying two successive inversions at f0 – f1 and f0 + f1, resulting in net reversal of the blood inversion in the control condition, while matching the MT effects of the tag condition because the same RF power is used. Although AM-CASL allows multislice acquisitions, the double inversion in the control condition is not ideal and leads to approximately 32% loss in inversion efficiency.10 Diagrams of single-slice and AM-CASL are shown in Figure 15.2.
Transit Delay
As can be seen in Eq. 5, the difference signal ΔMt has an exponential dependence on transit delay δ, which not
only changes with age and disease, but is also spatially variant within the brain. To minimize the effect of δ, a postlabeling delay, w, can be inserted between the end of the labeling period and image acquisition.3 As long as w > δ, inclusion of this term in the quantification model results in the following equation for ΔMt:
only changes with age and disease, but is also spatially variant within the brain. To minimize the effect of δ, a postlabeling delay, w, can be inserted between the end of the labeling period and image acquisition.3 As long as w > δ, inclusion of this term in the quantification model results in the following equation for ΔMt:
where the dependence of ΔMt on δ is now governed by the difference between T1a and T1app, which is small for gray matter, allowing further simplification of Eq. 8 by eliminating the exponential term containing δ. Importantly, this assumption does not hold for white matter where the difference between T1a and T1app is not negligible, leading to significant errors.11
 FIGURE 15.3. Basic schematic of a pulsed arterial spin labeling experiment. Size of the inversion or tag region is equivalent to the amount of inverted blood spins (and therefore perfusion signal). TR is defined as the time between successive inversion pulses, must be long enough for fresh blood spins to fill the inversion region. A gap is typically inserted between imaging and inversion regions to minimize slice profile interaction, so inversion time (TI) must be long enough for tagged blood spins to reach the imaging region. |
Pulsed Arterial Spin Labeling
PASL is the other main category of ASL. As the name suggests, it uses a short RF pulse rather than the long continuous RF employed by CASL to label inflowing blood spins. The short RF is applied to a thick inversion region to create a bolus of labeled blood, not unlike a bolus of contrast agent or microspheres. Using a short RF gives PASL several advantages over CASL: it reduces the specific absorption rate, so PASL is less challenging at high fields, and the lower RF power also means less MT effects, allowing a smaller gap between inversion and imaging regions (Fig. 15.3), thereby reducing signal loss due to T1 relaxation during arterial transit. However, the short RF pulse duration also means a smaller bolus, so PASL generally has lower sensitivity than CASL. It is also important to keep in mind that the ASL bolus is temporary, as the labeled blood begins to relax at the rate of blood T1 as soon as the labeling RF is turned off. A sufficient amount of time is necessary for this labeled blood to travel through the gap, enter the imaging region, and change the local magnetization by exchanging with tissue water. PASL was first demonstrated in 1992 by Kwong et al.,12 who used an inversion recovery sequence to demonstrate increased blood flow in the visual cortex during photic stimulation. The concept was further extended by others into two broad classes of PASL methods, which are discussed in detail below: flow-sensitive alternating inversion recovery (FAIR)13,14 and echo-planar imaging and signal targeting with alternating radiofrequency (EPISTAR).15
Flow-Sensitive Alternating Inversion Recovery
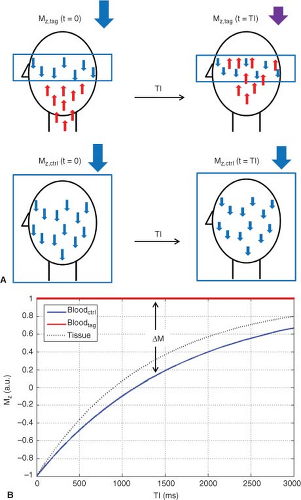
In FAIR, the tag condition is achieved by applying a slice-selective inversion pulse to the imaging region. This inverts the local tissue spins, but leaves the inflowing blood spins unchanged, creating positive perfusion contrast. The control condition uses the same inversion pulse without the slice-selective gradient to invert both tissue and blood spins, so there is essentially no perfusion contrast (Fig. 15.4A). To maintain a positive difference signal, ΔM is then defined as ΔM = Mt − Mc, where the subscripts t and c represent “tag” and “control,” respectively (Fig. 15.4B). This definition of tag and control makes FAIR slightly different from the conventional ASL definition, where the tag condition carries negative perfusion contrast. Occasionally, authors would adhere to the standard convention of ΔM = Mc − Mt, in which case ΔM would be negative.
Did you Know ThatBecause the inversion pulse used in FAIR is centered in the imaging region, the labeled bolus is present on either side of the imaging region, which makes FAIR sensitive to blood flow from both directions. In the brain, this can be a bit of a nuisance because venous blood is also labeled, but in other organs where incoming flow is not limited to a single direction, this is a unique advantage.
Did you Know ThatThe bolus size in FAIR is determined by the nonselective inversion, which is physically limited by the coverage of the transmit coil. Although this is not a problem for most studies today that use body coil transmission, surface coils or transmitting head coils limit the bolus size and therefore could potentially underestimate perfusion.
 FIGURE 15.4. (A) Diagram of tag (top) and control (bottom) conditions for flow-sensitive alternating inversion recovery (FAIR). Blue downward arrows represent inverted spins, whereas red upward arrows are uninverted spins. The net magnetization for each time point is represented by the thick blue or purple (owing to the presence of both positive and negative spins) arrows at the top of each figure. Notice the arrow is slightly shorter for Mctrl(t = TI) compared to Mctrl(t = 0) to represent loss of magnetization due to T1 relaxation during the duration inversion time (TI). Positive flow contrast is carried in the tag condition for FAIR, which is opposite to conventional arterial spin labeling. (B) Magnetization of blood in control and tag conditions and tissue as a function of TI. Due to T1 relaxation of blood, ΔM decreases with increasing TI. Tissue signal is canceled out in the subtraction and shown here just for reference. |
The control condition for FAIR can be implemented in different ways to minimize sources of error. For example, some studies have employed a delayed gradient technique, where the same slice-selective gradient used in the tag condition is applied after the inversion pulse in the control condition. This matches any eddy current effects between the two conditions so they can be canceled out in the subtraction. At the same time, the delayed gradient acts as a spoiler. Another variant of the control condition is to apply a very weak slice-selective gradient so that the labeled blood bolus width is not governed by the coverage of the body coil, which can be unnecessarily large, leading to increased large vessel contamination and requiring longer repetition times for the blood spins to relax before applying the next inversion pulse.16
Several variants of FAIR have been developed since it was introduced. One such variant is UNFAIR (Fig. 15.5B), which stands for uninverted FAIR.17 It has also been called extraslice spin tagging.18 UNFAIR applies two nonselective inversion pulses in the control condition, which causes all spins to experience a net 360-degree rotation, resulting in essentially no inversion. In the UNFAIR tag condition, the first inversion is selectively applied to the imaging region and the second inversion is nonselective. Thus, spins in the imaging region remains uninverted, while inflowing blood spins are inverted. ΔM is defined as
ΔM = Mc − Mt. A major advantage of UNFAIR is that the control image is essentially an M0 image without any flow contrast, which is needed for CBF quantification and is acquired separately for conventional FAIR. The authors suggested that it might not even be necessary to acquire the control image repeatedly, given that it is a true equilibrium image, thereby reducing the total acquisition time. Alternatively, the interleaved control image series can be used to assess the inherent blood oxygenation–level dependent (BOLD) contrast in simultaneous CBF/BOLD functional MRI (fMRI) studies. By ensuring both tag and control images are uninverted, UNFAIR also has the potential of reducing radiation damping errors associated with the varied T1 relaxation rates of the control and tag conditions for the conventional FAIR technique.19
ΔM = Mc − Mt. A major advantage of UNFAIR is that the control image is essentially an M0 image without any flow contrast, which is needed for CBF quantification and is acquired separately for conventional FAIR. The authors suggested that it might not even be necessary to acquire the control image repeatedly, given that it is a true equilibrium image, thereby reducing the total acquisition time. Alternatively, the interleaved control image series can be used to assess the inherent blood oxygenation–level dependent (BOLD) contrast in simultaneous CBF/BOLD functional MRI (fMRI) studies. By ensuring both tag and control images are uninverted, UNFAIR also has the potential of reducing radiation damping errors associated with the varied T1 relaxation rates of the control and tag conditions for the conventional FAIR technique.19
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
