Fig. 1
The feature space is defined by the cross-section center position x = (x 1, x 2, x 3), the cross-section tangential direction Θ = (θ 1, θ 2, θ 3) and the lumen pixel intensity distribution p vessel
2 Segmentation Model & Theoretical Foundations
2.1 Vessel Model & Particle Filters
To explain our method at a concept level, let us assume that a segment of the vessel has been detected: a 2D shape on a 3D plane. Similar to region growing and front propagation techniques, our method aims to segment the vessel in adjacent planes. To this end, one can consider the hypotheses ω of the vessel being at a certain location (x), having certain orientation (Θ), and referring to certain shape – an elliptic model is a common choice (є) – with certain appearance characteristics (p vessel ).
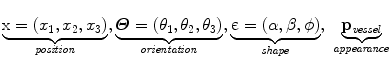
Then, segmentation consists in finding the optimal parameters of ω given the observed 3D volume. Let us consider a probabilistic interpretation of the problem with π(ω) being the posterior distribution that measures the fitness of the vector ω with the observation. Under the assumption that such a law is present, segmentation consists in finding at each step the set of parameters ω that maximizes π(ω). However, since such a model is unknown, one can assume an autoregressive mechanism that, given prior knowledge, predicts the actual position of the vessel and a sequential estimate of its corresponding states. To this end, we define:
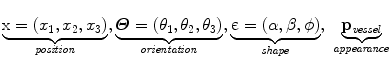
(1)
an iterative process to predict the next state and update the density function, that can be done using a Bayes sequential estimator and is based on the computation of the present state ω t pdf of a system, based on observations from time 1 to time t z 1:t : π(ω t |z 1:t ). Assuming that one has access to the prior pdf π(ω t−1 |z 1:t−1), the posterior pdf π(ω t |z 1:t ) is computed according to the Bayes rule:
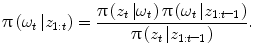
a distance between prediction and actual observation, based on the observation.
Simple parametric models will be suceptible to fail with vessels’ irregularities (pathologies, prosthesis, …). Therefore instead of optimizing a single state vector, multiple hypotheses are generated and weighted according to actual observation. Nevertheless, in practical cases, it is impossible to compute exactly the posterior pdf π(ω t |z 1:t ). An elegant approach to implement such a technique refers to the use of particle filters where each given hypothesis is a state in the feature space (or particle), and the collection of hypothesis is a sampling of the feature space.
Particle Filters [1, 8] are sequential Monte-Carlo techniques that are used to estimate the Bayesian posterior probability density functions (pdf ) [16, 34]. In terms of a mathematical formulation, such a method approximates the posterior pdf by M random measures {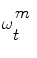
, m = 1..M } associated to M weights {
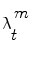, m = 1..M }, such that
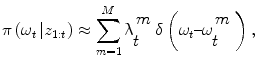
where each weight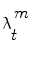 
reflects the importance of the sample 
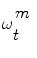in the pdf. The samples 
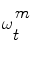are drawn using the principle of Importance Density [9], of pdf 
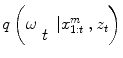and it is shown that their weights 
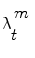are updated according to
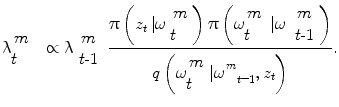
Once a set of samples has been drawn,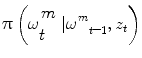 
can be computed out of the observation z t for each sample, and the estimation of the posteriori pdf can be sequentially updated.
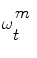, m = 1..M } associated to M weights {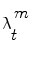, m = 1..M }, such that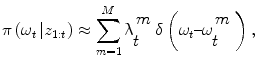(2)
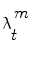reflects the importance of the sample 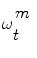in the pdf. The samples 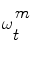are drawn using the principle of Importance Density [9], of pdf 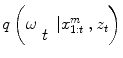and it is shown that their weights 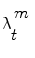are updated according to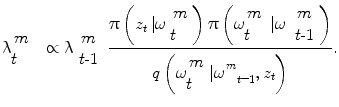(3)
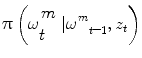can be computed out of the observation z t for each sample, and the estimation of the posteriori pdf can be sequentially updated.2.2 Prediction & Observation: Distance
This theory is now applied to vessel tracking. Each one of the particles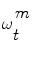 
represents a hypothetic state of the vessel; a probability measure 
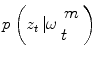is used to quantify how the image data z t fits the vessel model 
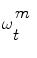. To this end, we are using the image terms, and in particular the intensities that do correspond to the vessel in the current cross-section. The vessel’s cross-section is defined by the hypothetic state vector (see Eq. (1)) with a 3D location, a 3D orientation, a lumen’s diameter and a pixel intensity distribution model (the multi-Gaussian). The observed distribution of this set is approximated using a Gaussian mixture model according to the Expectancy-Maximization principle. Each hypothesis is composed by the features given in Eq. (1), therefore, the probability measure is essentially the likelihood of the observation z, given the appearance A model. The following measures (loosely called probabilities) are normalized so that their sum over all particles is equal to one. Assuming statistical independence between shape S and appearance model A, p(z t |ω t ) = p(z t |S)p(z t |A).
Get Clinical Tree app for offline access
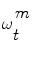represents a hypothetic state of the vessel; a probability measure 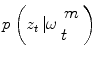is used to quantify how the image data z t fits the vessel model 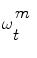. To this end, we are using the image terms, and in particular the intensities that do correspond to the vessel in the current cross-section. The vessel’s cross-section is defined by the hypothetic state vector (see Eq. (1)) with a 3D location, a 3D orientation, a lumen’s diameter and a pixel intensity distribution model (the multi-Gaussian). The observed distribution of this set is approximated using a Gaussian mixture model according to the Expectancy-Maximization principle. Each hypothesis is composed by the features given in Eq. (1), therefore, the probability measure is essentially the likelihood of the observation z, given the appearance A model. The following measures (loosely called probabilities) are normalized so that their sum over all particles is equal to one. Assuming statistical independence between shape S and appearance model A, p(z t |ω t ) = p(z t |S)p(z t |A).
Probability measure for shape based on contrast
Given the vessel model (see Eq. (1)), whose parameters are specified by the particle ω t , a measure of contrast, that we call the ribbon measure R, is computed:
The probability of the observation given the shape model is then computed:
![$$ \left\{\begin{array}{ll} R=-\infty,&{\mu}_{\mathit{int}}\le {\mu}_{\mathit{ext}} \\[4pt] R=\frac{\mu_{\mathit{int}}\mathit{\hbox{--}}{\mu}_{\mathit{ext}}}{\mu_{\mathit{int}}+{\mu}_{\mathit{ext}}},& \mathit{otherwise} \end{array}\right. $$](/wp-content/uploads/2016/09/A151032_1_En_14_Chapter_Equ4.gif)
(4)
where R 0 is a normalizing constant (the average value of R from ground truth), μ int is the mean intensity value for the voxels in the vessel, and μ ext is the intensities mean value for the voxels in a band outside the vessel, such that the band and the vessel’s lumen have the same area. This measure is normalized to be equivalent to model a probability measure. Since the coronary arteries are brighter than the background, the best match maximizes R.
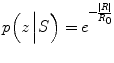
(5)
Probability measure for appearance
For the vessel lumen pixels distribution p vessel Eq. (1), the probability is measured as the distance between the hypothesized distribution and the distribution actually observed.
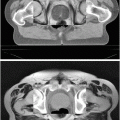
The distance we use is the symmetrized Kullback-Leibler distance D(p, q) between the model p(x) = p vessel and the observation q(x):
