Fig. 14.1
Schematic interaction among the main components constituting a registration method
Solving a specific registration problem requires careful selection of the individual components, parameters, and preprocessing procedures that together form a registration method. Given two images to be registered, one of the first such choices is concerned with which image should represent the fixed image. In the ideal case, the registration method should be inverse consistent, i.e., provide the same results independent on the selection of the fixed image. However, in practice most of the registration methods available will not provide identical solutions [9, 10], mainly because most similarity measures are not designed to be symmetric with respect to the images. The images will typically have different resolution and, in some applications, different dimensionality. When the differences in image resolution are significant, it can be beneficial to choose the moving image such that it has the higher spatial resolution. Finally, the choice of the fixed image is often dictated by the needs of the clinical application. As an example, resolution of PET images is typically inferior to that of MRI. However, structural images of the anatomy provided by the MR are used as a reference for radiological review of the various additional types of imaging.
Preprocessing of the input images can be applied to simplify the registration problem. Blurring and denoising of the images can discard the high-frequency components from the data, leading to reduced interpolation errors during image resampling [11], and prevent the optimization procedure to be trapped in local minima of the similarity measure. Various approaches can be used for equalizing intensities between the registered images (in particular, while registering MR images) [12] to improve the performance of the registration [13], especially when the simple sum of squared differences (SSD) similarity measure is used which assumes that homologous structures in the two images are depicted by the same image intensity. Inconsistent spatial inhomogeneities of the intensities over the image domain, such as those introduced due to the spatially varying sensitivity of the radiofrequency (RF) coils in MRI, may necessitate inhomogeneity bias correction [14, 15]. Preprocessing can also be used to emphasize certain image features [16]. Finally, limiting the calculation of the similarity metric to a certain region of interest in the image can improve the robustness of the method. As an example, segmentation of the brain volume, or skull-stripping [17], is often required for reliable co-registration in neuroimaging applications.
The degrees of freedom of the deformable registration, and, in turn, the computational burden associated with the optimization procedure, are determined by the transformation model used to represent the mapping between the registered images. A successful deformable registration is typically contingent on the successful rigid or affine alignment of the registered objects that must be completed prior to the modeling of the deformation. Transformation models that utilize various forms of spline functions have been utilized in a variety of image-based registration methods. B-splines are commonly used since they use local support and thus are less sensitive to the variation of the parameters over the image domain, enabling more flexible representation of localized deformations [18–20]. The flexibility of the B-spline model can be controlled by varying density of the control point grid, which facilitates multi-resolution registration schemes. Thin-plate spline transformations do not require regular sampling of the control points but are more sensitive to the local deformations since the interpolated displacement at any given point is affected by each of the control points [21].
A disadvantage of the spline-based methods is that they do not include any patient-specific modeling to produce realistic deformations of biological tissue. On the contrary, physically based methods use biomechanical models discretized by finite elements (FE) for including patient-specific modeling, e.g., mechanical properties of different biological tissue. The most popular approach is to model tissue deformations with an elastic model, and assuming infinitesimal strains leads to the computationally efficient linear elastic model. Dense transformation models, i.e., where a displacement vector is computed at every voxel such as in the Demons method [22], have a high number of degrees of freedom and can consequently model complex deformations but are also susceptible to unrealistic deformations and local foldings.
Nonrigid registration is a highly underdetermined problem, e.g., at each voxel in a 3D fixed image, a 3D displacement vector needs to be estimated to find the corresponding position in the moving image, and consequently we have three times as many unknowns as data points. The transformation model generally does not prevent folding or tearing of the deformation field, which can be characterized as nonphysical deformations that do not represent the deformation of typical human tissue. Typically, a regularizer is added to the registration objective function to properly constrain the problem to finding solutions that are physically plausible. Commonly, the regularizer aims at constraining the deformation to adhere to some physical properties. Depending on the underlying tissue to be registered, such properties can be smoothness, volume preservation, elastic [23–25], fluid [9], or hyper-viscoelastic [26]. Another popular means of constraining the deformation, especially in atlas-based registration, is to force the deformation and its inverse to be smooth functions, i.e., to be a diffeomorphism. Many methods are available, of which the most popular are the diffeomorphic demons [27] and the large deformation diffeomorphic metric mapping (LDDMM) [28, 29].
The similarity measures used in rigid registration are typically applicable in deformable registration applications. The choice of the metric is based on the specifics of the registered modalities and the computational constraints imposed by the IGT application. Registration of the modalities that maintain consistent mapping of the image values, such as CT, can be feasible using simple metrics such as sum of squared differences. Information theoretic metrics, such as mutual information, have proven practical and robust in a variety of applications and modalities [30, 31]. Specific to deformable registration, template matching schemes [32] were proposed to improve the sensitivity of the metric to local deformations. Sampling of the full image domain for the purposes of evaluating the similarity metric is frequently not practical for time-critical IGT applications; various sampling strategies have been investigated to reduce the computational burden while maintaining or improving smoothness of the cost function [33, 34]. Some of the popular optimization approaches used for registration purposes were surveyed by Maes et al. [35].
Validation of the results produced by the deformable registration methods is significantly more challenging than for the problems that involve linear transformations. In the context of IGT, the question of primary interest is the registration error in the area of clinical interest. Such estimations typically require identification of homologous points that correspond to the salient image structures that can be consistently identified in both images. Such points can correspond to the intrinsic anatomical features that can be identified in a population of patients [36, 37], subject-specific image features, such as calcifications in the prostate imaging [16], or implanted markers [38]. Localization of such homologous points is typically done by a domain expert, and the registration errors should be considered in comparison with the feature localization errors. Reliable and consistent identification of the corresponding features is not always feasible due to the limited resolution, lack of localized image features, and the fact that the registered images often provide complementary information about the imaged anatomy, and the features present in one modality may not be reliably identifiable in the other image. Therefore, digital [39] and physical phantoms [40, 41] that can model realistic deformations of the studied organ are often employed. Measures based on the overlap of the corresponding segmented structures (such as Dice and Jaccard metrics) [42] and the Hausdorff distance [43] have also found applications in assessing the results of NRR methods.
Precise quantification of the absolute error in an arbitrary region of the image domain is often not possible because of the lack of ground truth and difficulties in identifying corresponding image features. In such situations characterization of the registration algorithm performance may still be possible by quantifying the uncertainty in the registration result. In point-based rigid body registration, registration uncertainty has been studied extensively to quantify the distribution of the target registration error (TRE) [1, 2, 44], which can be important for the surgeon, for instance during image-guided biopsies. Conversely, in nonrigid intraoperative registration, registration uncertainty is mostly neglected, and research has been focused on finding the most likely point estimate of the registration problem. In the case of neurosurgery, because of intensity differences due to contrast enhancement, degraded image quality and missing data due to resection, the registration uncertainty will increase in and around the resection site [45]. Therefore, reporting both registration uncertainty and the most likely estimate can potentially provide the surgeon with important information that affect the understanding of the registration results and consequently the decisions made during surgery, especially when the tumor is adjacent to important functional areas.
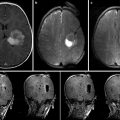
For intensity-based nonrigid registration, few methods are available for estimating the registration uncertainty. Kybic [46] models images as random processes and proposed a general bootstrapping method to compute statistics on registration parameters. Hub et al. [47] developed a heuristic method for quantifying uncertainty in B-spline image registration by perturbing the B-spline control points and analyzing the effect on the regional similarity criterion. In Simpson et al. [48], the posterior distribution on B-spline deformation parameters were modeled with local Gaussian distributions and approximated by a variational Bayes method. It was shown that utilizing the registration uncertainty in classification of Alzheimer patients improved the classification results. Gee et al. [49] described a Bayesian approach to uncertainty estimation, where the posterior distribution, composed of local Gaussian approximations of the likelihood term and a linear elastic prior, was explored with a Gibbs sampler. Another Bayesian approach was taken by Risholm et al. [50] which used Markov chain Monte Carlo (MCMC) to characterize the posterior distribution on registration parameters which does not require any (Gaussian) approximations to the posterior distribution. Because registration likelihood terms must depend on the complicated spatial structure of images, they are generally highly non-convex with respect to the deformation parameters, thus the assumption that the posterior distribution is unimodal and Gaussian is suspect. Recent results [51] demonstrate that the distribution on registration results may be multimodal and have heavier tails than Gaussian distributions, reflecting the possibility of results that are essentially outliers. In Risholm et al. [45] methods were introduced for summarizing and visualizing the registration uncertainty in the case of neurosurgery for tumor resection, and it was demonstrated that uncertainty information is important to convey to a surgeon when eloquent areas are located close to the resection site. An example of the uncertainty associated with registration results when registering pre- with intraoperative MRI of the brain is included in Fig. 14.2.
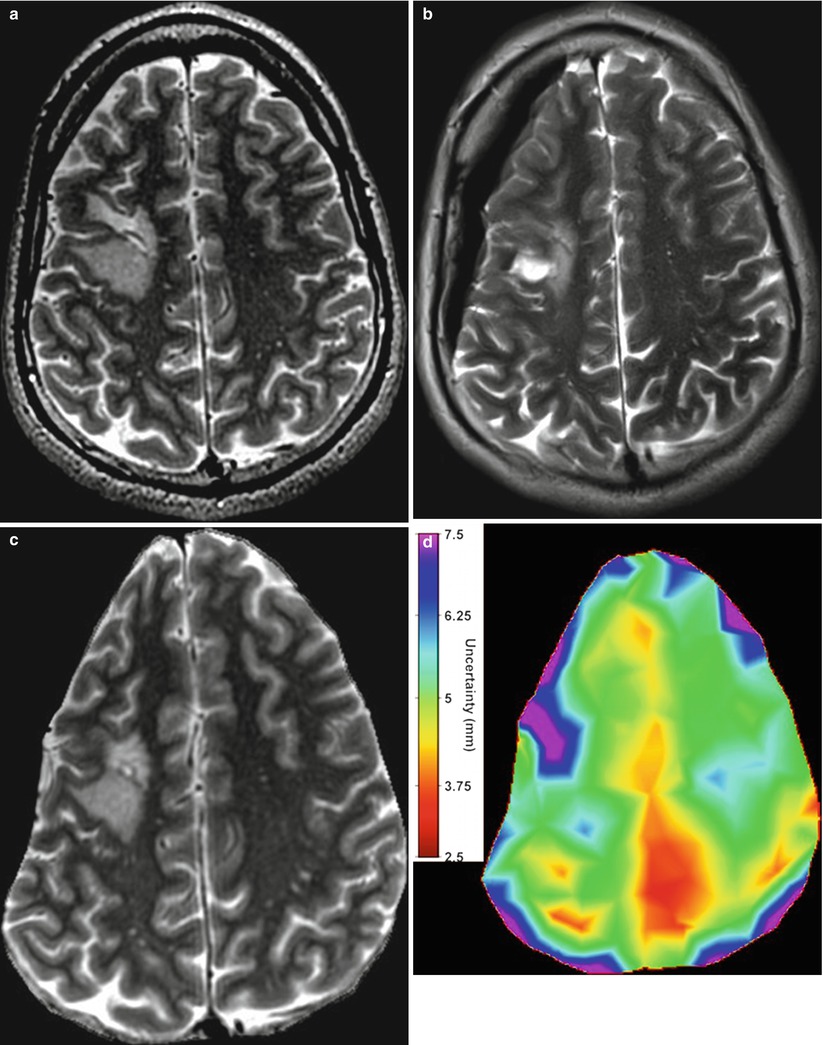

Fig. 14.2
(a) An axial slice of the preoperative MRI. Notice the tumor in the middle left of the image. (b) Corresponding axial slice of the intraoperative MRI. (c) Registered version of (a) to match (b) computed with the Bayesian registration framework by Risholm et al. [45]. The registration uncertainty, i.e., for each voxel in the image in (c), a corresponding spatial uncertainty has been estimated and is depicted in (d). Notice the increased uncertainty around the tumor site
IGT Applications
Image-Guided Neurosurgery
The aim of a neurosurgical resection is to maximize the removal of pathological tissue while preserving healthy and important functional brain tissue. MRI plays an important role in planning neurosurgical procedures because it can provide high-resolution anatomical images that can be used to discriminate between healthy and tumor tissue, as well as assist in identifying the location and extent of the functional areas. If important functional areas are touched or removed during surgery, it can have an adverse effect on the patient’s quality of life postsurgery. Ideally, surgeons aim for resection margins of 0.5–1 cm around the most critical functional areas. Therefore, it is especially important to identify eloquent areas when they are located adjacent to the resection site because it facilitates creating a map of important anatomical structures and surrounding functional areas which the surgeon can use to plan the procedure [52]. In the past decade, several groups investigated the use of intra-procedural MRI as a means for guiding resection and established its value for optimizing the extent of resection [53]; however, intra-procedural MRI does not in general provide any information regarding the location of eloquent areas.
Registration of the structural brain MRI scans historically attracted most of the attention of the researchers in NRR. Some of the earliest approaches proposed for image-guided interventions were motivated and evaluated in the context of clinical applications in neurosurgery, such as neurosurgical planning and compensation of the brain shift [54]. Nowadays, digital phantoms [55, 56], validation datasets, and a variety of publicly available registration tools [57, 58] targeting brain MRI analysis and registration are available and can be used as a reference for the development of the new methods. Deformable registration technology that involves multiple modalities and applied to the organs other than brain is in general less developed.
Most current neuronavigation software registers preoperative images to the intraoperative space using landmarks with a rigid transformation [2]. However, a common occurrence during neurosurgery is brain shift [54, 59, 60], i.e., a nonrigid deformation of the brain tissue which occurs after the craniotomy and opening of the dura, and is caused by various combined factors: cerebrospinal fluid (CSF) leakage, gravity, edema, tumor mass effect, and administration of osmotic diuretics. Reported deformations of the brain tissue due to brain shift are up to 24 mm [61–63], and further deformations may be induced because of manipulation of tissue during the resection [4, 64]. Figures 14.2 and 14.3 show some typical examples of brain shift caused by opening of dura. Consequently, the preoperative map does not necessarily reflect the intraoperative anatomy the surgeon observes during surgery.
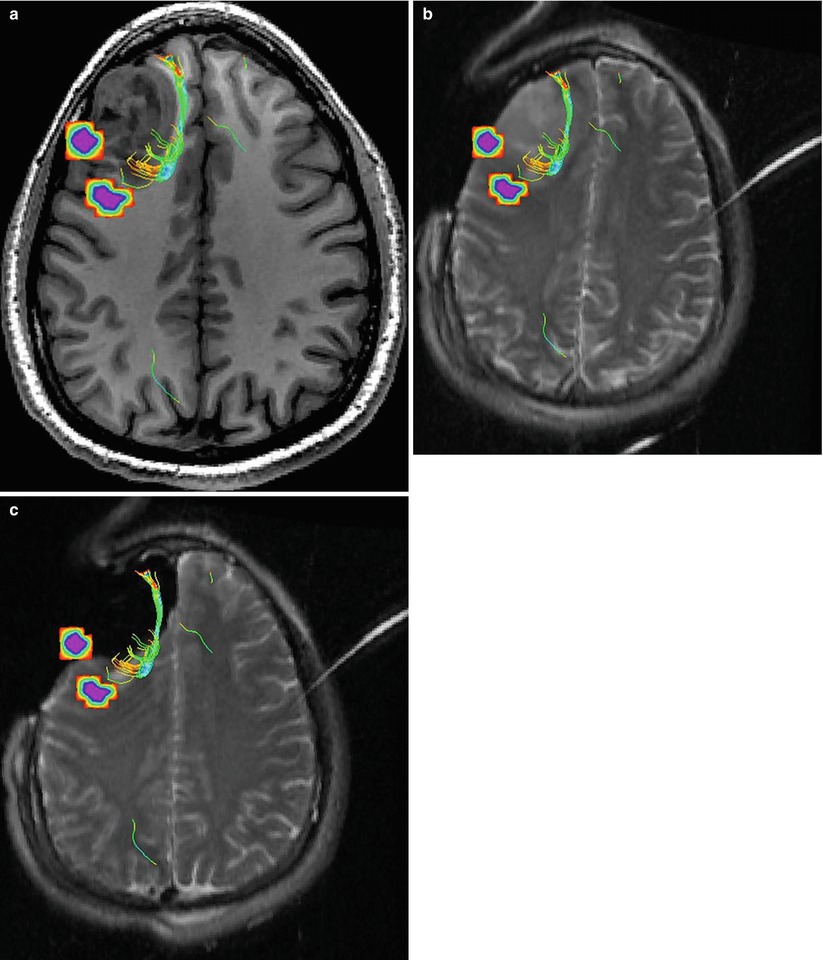

Fig. 14.3
(a) Preoperative MR image overlaid with diffusion fiber tracts and fMRI-activated areas depicting language areas. Notice the proximity of the white matter fiber tracts and the language area to the tumor. (b) An intraoperative image acquired after craniotomy and opening of dura. The image has been rigidly registered to the image in (a). Because of brain shift, the location of the functional information that resides in the planning MR image space may not reflect the anatomy seen during surgery. (c) An intraoperative image, rigidly registered with image in (a), after resection. Because of the nonrigid changes to the brain during surgery, the current location of the functional information may not reflect the current location, and the functional information should not be trusted until they have been nonrigidly aligned with the intraoperative anatomy (The figure uses the neurosurgical planning training dataset available at http://www.slicer.org/slicerWiki/images/9/9c/Slicer-tutorial-neurosurgery_slicer3.6.1.zip)
As a way of acquiring up-to-date anatomical information during surgery, ultrasound [65, 66] and intraoperative MRI [67, 68] are the most commonly used imaging modalities, and it has been shown that intraoperative imaging during neurosurgery leads to a significant increase in the extent of tumor removal and survival times [69]. However, because intraoperative functional information is difficult to acquire, nonrigid intraoperative registration has been introduced as a way of mapping the preoperative functional information into the intraoperative space such that the preoperative map reflects the intraoperative anatomy. Consequently, based on the aligned image information, the approximate intraoperative boundaries between tumor tissue, healthy tissue, and, perhaps most importantly, the functional areas can be determined as they are not directly visible to the surgeon. Archip et al. [43] showed a statistically significant improvement in alignment accuracy when using nonrigid registration compared to the standard clinical practice of rigid registration.
A variety of FE-based registration methods have been proposed for recovering intraoperative brain deformation. Such approaches can in general be divided into two groups: those that use the image intensities as the driving force in the registration [23, 67] and those that use sparsely measured displacements, either through landmarks, such as cortex and ventricle surfaces extracted from images [59, 70], or externally measured displacement using, for instance, laser scanners [71], stereovision [72], or alternatively some combination of intensities and landmarks [73, 74]. Other sophisticated models that can handle large deformations such as hyper-viscoelastic models [26], or coupling of fluid and elastic models [75], have also been investigated. Biomechanical models of brain deformations [23, 71] require specifying separate material parameters, e.g., to distinguish between CSF and white and grey matter, which are related to the regularization of the registration [45]. Because the literature reports divergent values for the material parameters [75], most authors heuristically set these parameters. Estimation of the uncertainty in these parameters has been attempted for registration of brain images [48, 76].
Intraoperative images used in intensity-based registration of the brain scans are often of a degraded quality compared to the preoperative images, which can increase the uncertainty of the registration, reduce the convergence factor, and increase the chance of estimating an incorrect deformation because the algorithm might end up in a local minimum of the optimization landscape. Clatz et al. [23] introduced a robust block matching algorithm that uses a trimmed least squares approach to improve the robustness of the algorithm to for instance local intensity differences. Guimond et al. [77] extended the demons method to handle intensity differences by adding an affine intensity matching step. If the intensity differences are of a global character, for instance due to different imaging parameters, robust similarity measures such as mutual information [78] can be used. Alternatively, using landmarks extracted from the images [59, 79, 80], or externally measured displacements [72, 81], circumvents the use of image intensities completely.
The majority of nonrigid registration research assumes a bijective deformation field and regularizes the deformation field accordingly. With a few notable exceptions, researchers have usually not included models for accommodating the non-bijectivity that is caused by retraction and resection [64]. Periaswamy and Farid [82] proposed a registration framework which handles missing data by applying a variation of the expectation-maximization method to alternately estimate the missing data and the registration parameters. A biomechanical approach was taken by Miga et al. [71] that explicitly handles resection and retraction. The FE mesh was split along the retraction, while nodes in the area of resection were decoupled from the FE computations. The main drawback of using a conventional FE method for modeling retraction and resection is that it requires re-meshing. Inspired by recent developments in the field of fracture mechanics, Vigneron et al. [83] introduced the extended FE method for modeling discontinuities resulting from retraction and resection. In Risholm et al. [84], the popular demons method was extended to accommodate tissue resection and retraction through anisotropic regularization.
The time constraints of an intraoperative registration algorithm are strict and usually considered to be the period of time from the end of image acquisition until the surgeon is ready to continue the operation. Computer hardware designed for fast parallel computations is usually exploited to make registration algorithms fast enough for intraoperative use—by utilizing either graphic cards [85, 86] or large computational clusters [87].
Image-Guided Prostate Biopsy
Prostate cancer (PCa) is the second most diagnosed type of cancer and the sixth leading cause of cancer death in males worldwide [88]. Incidence of PCa increases with age, and in many instances it is a slow-progressing disease that is not life threatening. One of the challenges in the management of PCa is therefore to accurately determine the aggressiveness and stage of the disease so that the appropriate treatment can be prescribed and unnecessary complications can be avoided. Magnetic resonance imaging (MRI) plays an important role in detection and staging PCa [89]. There is strong evidence that multiparametric MRI (mpMRI) protocols that include diffusion-weighted, dynamic contrast-enhanced (DCE) MRI and magnetic resonance spectroscopy imaging (MRSI) can significantly improve both detection and characterization of PCa [90]. These observations motivated research efforts towards using mpMRI to improve the accuracy of PCa diagnosis and treatment. One such application of mpMRI is to direct the PCa needle biopsy towards the suspicious location of the prostate [91].
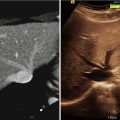
Targeted image-guided approaches to prostate biopsy have now been investigated by several groups [91–95], aiming sampling of the tissue from the cancer-suspicious regions by combining the superior ability of MRI to demonstrate prostate cancer with excellent spatial resolution of prostate anatomy and the visualization of the biopsy needle. Unfortunately, mpMRI protocols are too time consuming to be feasible during such procedures and require detailed image processing and analysis to identify suspicious targets; see Fig. 14.4. In such approaches, suspected cancer areas are usually localized in each of the individual parameter images prior to biopsy, based upon diagnostic MRI exam. Reidentification of the these areas during the MRI-guided interventions can be done by means of visual assessment [95] or by manual alignment of the diagnostic anatomical scan with the intra-procedural image [93]. However, such operator-centric approaches can be time consuming and require specialized training in interpretation of prostate MRI, leading to additional complexity of the procedure. Moreover, they do not account for prostate deformation due to the deformation induced by the endorectal coil and changes in the patient position [96, 97]. This motivates automated registration of the diagnostic mpMRI with the intra-procedural imaging to direct biopsy sampling for improved accuracy. In such scenario, intra-procedural imaging is performed using either ultrasound or fast MR imaging, and the pre-procedurally acquired mpMRI is registered to enable reidentification of the suspicious areas.
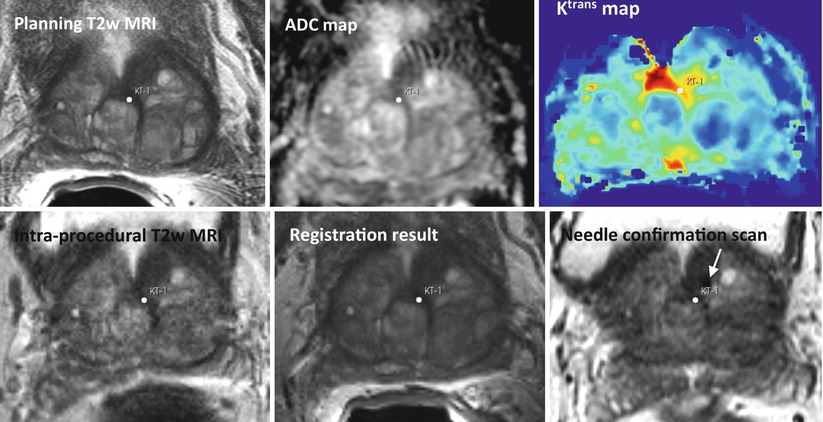

Fig. 14.4
Top row: pre-procedural MRI scans used for identifying the cancer-suspicious prostate areas (T2w MRI, apparent diffusion coefficient (ADC) map derived from diffusion-weighted MRI, and modeled volume transfer constant between the blood plasma and the extravascular extracellular space, Ktrans). Note the suspicious area marked with a white point. Bottom row: intra-procedural T2w MRI, pre-procedural T2w MRI registered to the intra-procedural anatomy, needle confirmation scan. The planned biopsy target location was warped using the deformable transformation derived by NRR. White arrow points to the needle artifact in the proximity of the planned biopsy location
Several approaches to nonrigid image registration for compensating prostate deformation have been proposed. Bharatha et al. developed a registration approach that relies on the alignment of the segmented prostate gland surfaces [98]. The registration is accomplished by the initial rigid alignment of the gland and establishing the correspondence between the surface points using the active surface algorithm [99]. Finite element modeling was next applied to propagate the surface displacement throughout the prostate volume. An alternative methodology for establishing surface correspondence that relies on conformal mapping was proposed by Haker et al. [100]. The concept of using biomechanical modeling for recovering prostate deformations was further advanced by Hensel et al. [101] who proposed a formulation that enabled analysis of interaction among several adjacent organs. As mentioned earlier, there are several challenges associated with accurate biomechanical modeling of the deforming organs. Biomechanical properties for the modeled organs are typically not known, which can lead to inaccuracies of the FEM simulation [102]. Matching of the surface boundaries is challenging and requires accurate segmentation of the organ [103]. Approaches that attempt to quantify such uncertainties have been proposed [104], but their use during the procedure is typically not feasible due to long computation times.
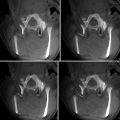
An alternative class of methods that was proposed for NRR of the deforming prostate relies on the image similarity metrics for determining the optimal alignment. Wu et al. utilized mutual information (MI) similarity metric to find the optimal coefficients of the polynomial transformation using the Newton–Raphson optimization scheme [105]. d’Aische et al. proposed a formulation that included image similarity together with the linear elastic energy of the FEM mesh [106]. Oguro et al. evaluated the utility of the MI-based registration and B-spline transformation model [107]. Fedorov et al. combined a hierarchical transformation model, see Fig. 14.5, with customized preprocessing and initialization to achieve deformable registration time compatible with the intra-procedural application during MR-guided biopsy procedures [108].
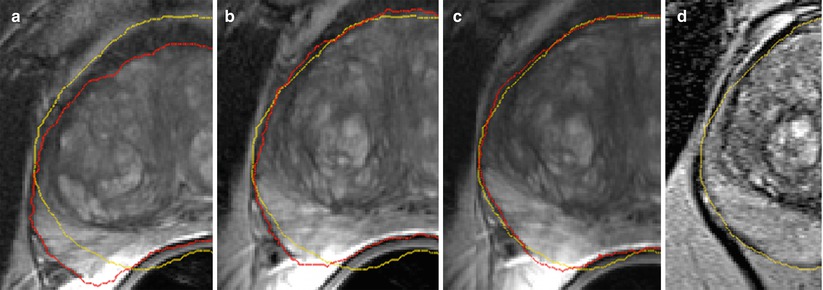

Fig. 14.5
Diagnostic T2w MRI warped to intra-procedural T2w MRI after rigid (a), affine (b), and B-spline (c) registration steps warped to the intra-procedural T2w MRI (d). Red and yellow show the fused contour of the warped prostate gland in the diagnostic MRI (red), and the contour of the gland in the intra-procedural MRI (yellow), respectively, is shown in the overlay. Note the gradual improvement in alignment of the prostate capsule boundary, PZ/CG interface, and the central gland BPH nodule
US is the modality most widely used for interventional prostate imaging. Integration of the versatile structural and functional information in the mpMRI with the cheap and readily available US imaging by means of image registration has been an active area of research. Mizowaki et al. [109] approached the problem of registering MRI to US/CT modalities by using manually identified points on the superior boundary of the gland and propagating the deformation over the gland volume. Since the appearance of the prostate gland in the ultrasound imaging is drastically different from MRI, a number of proposed registration approaches rely on the segmented boundary of the gland to achieve alignment [110, 111]. Xu et al. employed manual alignment of the planning MRI with the initial intra-procedural US imaging, followed by automatic intermittent correction of the prostate motion during the procedure by reregistration procedure that relied on SSD similarity metric [112]. Hu et al. proposed model-to-image registration framework based on the statistical model of the prostate deformation [16].
Performance evaluation of the NRR methods developed for the purposes of image-guided prostate interventions typically relies on the improvement in the overlap of the segmented anatomical regions of the gland [98, 107] and on the alignment of the corresponding patient-specific image features [16, 108]. Alignment of the image artifacts corresponding to the implanted fiducial markers was utilized by some of the studies [101]; however, this approach is not widely applicable due to its invasiveness.
Conclusions
In this chapter we introduced the reader to the basic concepts of nonrigid registration and discussed two of the clinical research applications where it has been studied to a large extent. We did not attempt to provide an all-encompassing survey of the registration technology—the interested reader is referred to the numerous surveys on the subject [4, 11, 113–115]. However, we hope that this text helped in appreciating the versatility and some of the capabilities of the registration tools. There are numerous challenges that remain to be solved in integrating these capabilities into the clinical workflow—lack of the validation ground truth being one of the major obstacles. However, it is clear that the various applications of nonrigid registration—such as image-guided interventions and minimally invasive surgeries, proliferation of the integrated multimodality operating suites, and development of quantitative biomarkers [116, 117]—will continue motivating refinement of the registration technology and its increasing use in the research applications.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree