(1)
Since lethal lesions are Poisson-distributed across a cell population, the probability that a large population of cells will undergo a certain number of lethal lesions (i.e., the surviving fraction, S) is given by:
![$$ S = \exp \;[ - \left( {\alpha D + G\beta D^{2} } \right)] $$](/wp-content/uploads/2016/09/A174_2012_684_Chapter_Equ2.gif)
![$$ S = \exp \;[ - \left( {\alpha D + G\beta D^{2} } \right)] $$](/wp-content/uploads/2016/09/A174_2012_684_Chapter_Equ2.gif)
(2)
The parameters α and β are the rates at which lethal lesions are generated per unit absorbed dose and absorbed dose squared, respectively. These depend upon the tissue type under consideration. G is the Lea-Catcheside time factor which accounts for DSB repair; since this repair requires time it effectively accounts for effects of dose-rate or fractionation on the lethal yield associated with dual DSBs. It was initially derived for specific special cases by Lea and Catcheside (Lea and Catcheside 1942) and subsequently generalized (Kellerer and Rossi 1972; Sachs et al. 1997; Millar 1991) to the following equation:
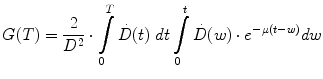
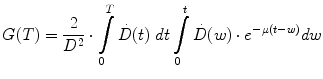
(3)
Equation 3 may be interpreted as accounting for the impact of DNA damage repair during the time-interval between the first and second DSB. The integrations are performed over time with a time-dependent dose-rate, 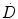 , as the integrand and T, the overall exposure time. The expression after the second integral reflects repair of the first DSB; the repair rate is given by the parameter, μ, in the exponential expression. The first integral refers to the second DSB which can interact with the first, partially repaired lesion (Brenner et al. 1998). The LQ model formulation presented above draws heavily from the description provided by Brenner, et al. (1998) in that the G time factor is explicitly included in the LQ model. In most descriptions of the LQ model, this term is not included initially, but rather invoked as an adjustment to reflect incomplete repair of DNA damage when the LQ model is applied to low dose-rate radiation. The formulation presented above includes the G time factor term from the beginning to highlight the generality of the LQ formalism and its applicability to low-dose rate, time-varying exposure, as occurs with RPT. Modifications to the LQ formalism that account for cell redistribution associated with the differential cell cycle sensitivity of cells as well as cellular proliferation have also been described (Jones and Dale 1995; Barendsen et al. 2001; Brenner et al. 1995; Travis and Tucker 1987; O’Donoghue 1991, 1997; O’Donoghue et al. 1995, 2000). In RPT, if the uptake phase of the dose-rate is assumed very rapid relative to a loss or decay phase, then integrating expression 3 from zero to complete decay of the radionuclide (T = ∞), gives the following expression for G:
, as the integrand and T, the overall exposure time. The expression after the second integral reflects repair of the first DSB; the repair rate is given by the parameter, μ, in the exponential expression. The first integral refers to the second DSB which can interact with the first, partially repaired lesion (Brenner et al. 1998). The LQ model formulation presented above draws heavily from the description provided by Brenner, et al. (1998) in that the G time factor is explicitly included in the LQ model. In most descriptions of the LQ model, this term is not included initially, but rather invoked as an adjustment to reflect incomplete repair of DNA damage when the LQ model is applied to low dose-rate radiation. The formulation presented above includes the G time factor term from the beginning to highlight the generality of the LQ formalism and its applicability to low-dose rate, time-varying exposure, as occurs with RPT. Modifications to the LQ formalism that account for cell redistribution associated with the differential cell cycle sensitivity of cells as well as cellular proliferation have also been described (Jones and Dale 1995; Barendsen et al. 2001; Brenner et al. 1995; Travis and Tucker 1987; O’Donoghue 1991, 1997; O’Donoghue et al. 1995, 2000). In RPT, if the uptake phase of the dose-rate is assumed very rapid relative to a loss or decay phase, then integrating expression 3 from zero to complete decay of the radionuclide (T = ∞), gives the following expression for G:
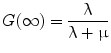
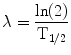
 , as the integrand and T, the overall exposure time. The expression after the second integral reflects repair of the first DSB; the repair rate is given by the parameter, μ, in the exponential expression. The first integral refers to the second DSB which can interact with the first, partially repaired lesion (Brenner et al. 1998). The LQ model formulation presented above draws heavily from the description provided by Brenner, et al. (1998) in that the G time factor is explicitly included in the LQ model. In most descriptions of the LQ model, this term is not included initially, but rather invoked as an adjustment to reflect incomplete repair of DNA damage when the LQ model is applied to low dose-rate radiation. The formulation presented above includes the G time factor term from the beginning to highlight the generality of the LQ formalism and its applicability to low-dose rate, time-varying exposure, as occurs with RPT. Modifications to the LQ formalism that account for cell redistribution associated with the differential cell cycle sensitivity of cells as well as cellular proliferation have also been described (Jones and Dale 1995; Barendsen et al. 2001; Brenner et al. 1995; Travis and Tucker 1987; O’Donoghue 1991, 1997; O’Donoghue et al. 1995, 2000). In RPT, if the uptake phase of the dose-rate is assumed very rapid relative to a loss or decay phase, then integrating expression 3 from zero to complete decay of the radionuclide (T = ∞), gives the following expression for G:
, as the integrand and T, the overall exposure time. The expression after the second integral reflects repair of the first DSB; the repair rate is given by the parameter, μ, in the exponential expression. The first integral refers to the second DSB which can interact with the first, partially repaired lesion (Brenner et al. 1998). The LQ model formulation presented above draws heavily from the description provided by Brenner, et al. (1998) in that the G time factor is explicitly included in the LQ model. In most descriptions of the LQ model, this term is not included initially, but rather invoked as an adjustment to reflect incomplete repair of DNA damage when the LQ model is applied to low dose-rate radiation. The formulation presented above includes the G time factor term from the beginning to highlight the generality of the LQ formalism and its applicability to low-dose rate, time-varying exposure, as occurs with RPT. Modifications to the LQ formalism that account for cell redistribution associated with the differential cell cycle sensitivity of cells as well as cellular proliferation have also been described (Jones and Dale 1995; Barendsen et al. 2001; Brenner et al. 1995; Travis and Tucker 1987; O’Donoghue 1991, 1997; O’Donoghue et al. 1995, 2000). In RPT, if the uptake phase of the dose-rate is assumed very rapid relative to a loss or decay phase, then integrating expression 3 from zero to complete decay of the radionuclide (T = ∞), gives the following expression for G: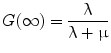
(4)
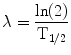
(5)
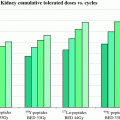
In Eq. 5, T 1/2 is the half-time for the reduction in dose-rate. If the dose contribution to a target from adjacent tissue can be neglected, this can be approximated as the clearance rate of the agent from the target tissue. Applying the same rapid uptake assumption an expression for finite radiation time intervals, T has also been defined and has been used in a radiobiological evaluation of renal toxicity (Wessels et al. 2008).
Following the derivation by Barendsen et al. (1982); Douglas and Fowler (1976); Dale (1985), Eq. 1 can be re-written as:
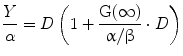
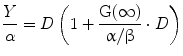
(6)
The term in the parentheses is referred to as the relative effectiveness, per unit dose, RE:
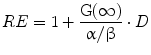
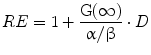
(7)
4.1 Biological Effective Dose
A new quantity can then be described, the BED:
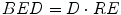
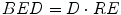
(8)
BED provides a reference dose rate to which total doses delivered with different dose rates may be related. The reference BED dose rate can be thought of as delivering infinitesimally small absorbed doses over an infinite time period. In fractionated external beam, the dose rate per fraction is high and there is no reduction in the yield of damage associated with two near simultaneous radiation events, accordingly, G(∞) = 1. Using this in Eqs. 7 and 8, one can derive the relative effectiveness per unit dose formula used in external beam formulations of fractionated radiotherapy (see MIRD Pamphlet 20 Wessels et al. (2008) and references (Dale 1985; Dale and Carabe-Fernandez 2005). In this context, the BED can be used to relate the expected biological effect of different fractionation schemes. For example, the tolerance dose to a particular organ obtained by a 2 Gy fractionation scheme would be lower for a 3 Gy fractionation scheme. By equating BED values and solving for the total dose, D, one could calculate the lower total dose. Illustration of this and the specific equations used are available in reference (Dale 1985). In RPT the dose rate varies temporally and a number of investigators have examined the implications of this on tumor control and normal tissue toxicity (Rao and Howell 1993; Howell et al. 1994; Mayer et al. 1995; Akabani et al. 2000; DeNardo et al. 2002; Flynn et al. 2001; Shen et al. 2002; Behr et al. 1998). Under the specific condition of a rapid initial uptake in the dose rate followed by exponential reduction over time, Eqs. 4 and 7 can be used to obtain the following expression for BED:
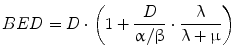
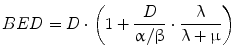
(9)
Equation 9 has recently been extended to incorporate the dose contribution from different source organs. The extended, MIRD schema-compatible formalism was applied to the analysis of red marrow and kidney toxicity for RPT (Baechler et al. 2008). In these cases, the dose rate increases rapidly and then falls off exponentially. If the rapid increase in dose rate does not apply, then the expression derived in (Howell et al. 1994), which specifically includes a difference of exponential functions to give a well-defined increasing phase in the dose-rate followed by an exponentially decreasing phase, can be used. In imaging-based patient-specific dosimetry that is performed on a voxel by voxel (or sub-region) basis, algebraic solutions to Eq. 3 are not feasible in the majority of cases. In these situations, BED may still be implemented using a methodology recently developed, specifically for this purpose (Hobbs and Sgouros 2009). The method can be applied for piece-wise defined descriptions of the dose-rate such as are used in the trapezoidal integration of dose rate to obtain total absorbed dose.
The interest in incorporating radiobiological modeling in the assessment of tissue toxicity and tumor response for RPT was initially driven by the desire to understand renal toxicity results in radiopeptide and small molecule therapy wherein large activity administrations of a rapidly clearing agent can lead to very high initial dose rates, leading to a dose-rate profile potentially higher than that observed in external radiotherapy from which kidney tolerance doses are derived (Wessels et al. 2008; Barone et al. 2005; Bodei et al. 2008; Emami et al. 1991; Bentzen et al. 2011). In addition, interest in combining radiotherapy with RPT and the corresponding requirement to reconcile absorbed doses that are delivered at fractionated high dose-rates with generally lower, exponential decreasing, dose rates has provided further impetus for the incorporation of BED into patient-specific treatment (Bodey et al. 2004; Hobbs et al. 2011).
4.2 Equivalent Uniform Dose
The uniformity (or lack thereof) of absorbed dose distributions and their biological implications has been examined intensively, primarily in animal studies (O’Donoghue 1999, 2000; Roberson et al. 1994; Muthuswamy et al. 1996; Flynn et al. 2003; Howell et al. 1989; Humm and Cobb 1990; Flynn et al. 2001, 2002). To address the question of how to best represent the large amount of data in 3-D distributions of absorbed dose, one may look to the radiotherapy field and use dose-volume histograms to represent dose distributions in targeted radionuclide therapy (Kolbert et al. 1994).
The BED formulation enables comparison of absorbed doses obtained from different temporal dose-distributions by relating the biological effect of a given absorbed dose to the expected effect if the dose were delivered at infinitesimally small dose fractions delivered over an infinite amount of time; the EUD formulation similarly relates different spatial dose distributions by relating the biological effect of a given mean absorbed dose to the expected effect if the dose were uniformly distributed throughout the tissue volume (O’Donoghue 1999; Niemierko 1997).
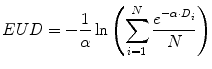
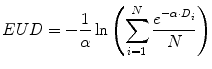
(10)
This provides a single value that may be used to compare different dose distributions; the value also reflects the likelihood that the magnitude and spatial distribution of the absorbed dose is sufficient for tumor kill. Note that a more elaborate expression of the EUD exists which incorporates the full time-dependent effects (Niemierko 1997); the equation presented here assumes no quadratic dose effect. The concept (and value) of EUD is illustrated by considering a tumor in which one-half of the volume receives a dose of 100 Gy and the other half receives 0 Gy. Such an absorbed dose distribution would lead to treatment failure since the tumor half not exposed to radiation would re-grow. In this case, the absorbed dose delivered uniformly throughout the tumor volume (i.e., the EUD) would be close to zero in order to be consistent with the expected biological effect of the dose distribution described above. The illustration should also make it clear that EUD is not valid for normal organs since normal organs have a structural organization (i.e., 100 Gy to even a small portion of the spine can lead to paralysis; in contrast, 100 Gy to a large portion of the liver may be inconsequential since the liver can regenerate). Calculation of EUD requires knowledge of the radiosensitivity of the tumor and the assumption that all elements of the tumor are clonogenic. A technique similar to EUD that incorporates the normal tissue complication probability (NTCP) associated with irradiating different fractions of a normal organ volume has been described for a EUD formalism applicable to normal organs (Lyman and Wolbarst 1987; Burman 1991; Kutcher 1991). The initial EUD formulation incorporated the radiobiologic implications of dose delivered in 2 Gy fractions. A combined BED/EUD formalism was later developed for RPT by O’Donoghue (1999).
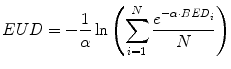
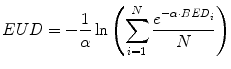
(11)
The application and corresponding equations for EUD as it is applied in patient-specific dosimetry are described in references (Prideaux et al. 2007; Hobbs et al. 2009), including the LQ formulation of Eq. 10. More recently the BED/EUD formalism has been applied to account for the effect of unlabeled antibody in the dose–response relationship in NHL (Dewaraja et al. 2010; Amro et al. 2010).
4.3 Caveats in Using Radiobiological Models
Like all models, radiobiological models are based on simplifying assumptions of underlying biological mechanisms and need to be applied with the understanding that their greatest strength is in providing guidance rather than in predicting the specific response in an individual patient. No single measurement or series of measurements are sufficient to declare a model completely validated, rather, model validation is an ongoing process in which an incremental approach is required to perform successive tests of the model under as wide a variety of conditions as possible. Each such test may be thought of as a confidence-building measure. Given enough tests, under different, clinically achievable and clinically relevant conditions, model validity may be inferred, but only within the scope of effects the model was designed to simulate. Every mathematical model excludes potentially relevant biologic processes. The implicit assumption is always that those processes that are not included in a given model have a minimal impact on the processes that are being simulated. Implementation of the BED and EUD models requires knowledge of the radiobiological parameters: α, β, and μ. To date, these radiobiological models have been applied using a single set of radiobiological parameters with the implicit assumption that a single set of values applies to the entire tumor or normal organ volume. In most cases, the parameters have been obtained from literature reports and are typically derived from a combination of animal and cell culture studies, supplemented by fitting of human response data when available. As is well-recognized, tumors are highly heterogenous and their radiosensitivity will vary in different tumor regions (e.g., hypoxic versus normoxic). Clonogenicity likewise will be variable throughout the tumor (i.e., dormant vs rapidly proliferating regions). It is also well-recognized that, in the majority of cases (unfortunately), patients receiving RPT have likely exhausted the cancer therapy armamentarium. Such heavy pre-treatment will impact normal organ function. Accordingly, both tumor and normal organ parameter applied can be expected to deviate from the true values in an individual patient. Nevertheless, tracers are being developed and clinically implemented that probe for radiosensitivity and proliferation and one may expect that such markers could be used to derive radiobiological parameter values to tumor and normal organ sub-volumes (Ribom et al. 2002; Vesselle et al. 2002).
Even with these caveats, it is important to recognize that the BED formalism has stood the test of time in radiotherapy and is likely to be useful in guiding activity administrations given tracer-based measurements of the clearance kinetics of a particular agent. The formalism also makes it possible to translate experience in radiotherapy to expected results in RPT. One may expect that such analyses, even on an individual patient basis will become more important as lower molecular weight agents continue to be implemented clinically. Likewise, EUD is useful in comparing different tumor absorbed dose distributions in a patient trial population or in comparing the potential impact of differences in the penetration characteristics of different RPT agents. On an individual patient basis an EUD value can provide a general assessment of the likelihood of tumor response given the agents spatial absorbed dose distribution in tumor.
5 Patient-Specific Dosimetry in Radiopharmaceutical Therapy of Previously Treated Patients
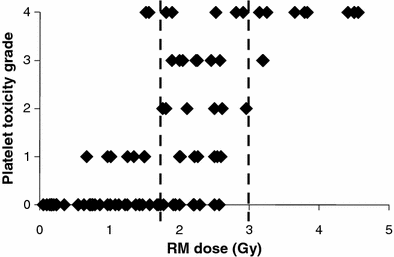
In the treatment of Non-Hodgkin’s lymphoma (NHL) with RPT, there is evidence that patient-specific dosimetry can better predict tumor response in previously untreated patients (Koral et al. 2003) than in a population of previously treated patients (Sgouros et al. 2003). In a recent analysis of NHL patients treated with either 131I- or 90Y-labeled anti-CD20 antibody, time since last chemotherapy was found to be the best predictor of hematologic toxicity (Baechler et al. 2008). In a compilation of marrow dose–response data for131I-labeled antibodies obtained from the literature (Fig. 1), it was possible to identify demarcation lines at 1.75 Gy and 3 Gy, below and above which minor or major platelet toxicity, respectively may be expected. Toxicity responses in the region between 1.75 and 3 Gy spanned the full range of platelet toxicities. In this region, red marrow absorbed dose is not the primary determinant of response; rather it is likely that the prior treatment history of each patient and their associate marrow reserve dictate the platelet toxicity response. Accordingly, the use of a biological marker of marrow reserve has been reported to improve the dose–response relationship (Siegel et al. 2003).