Dynamic Contrast-Enhanced Perfusion CT: Basics of Mathematical Tracer Kinetic Models and Applications
Kenya Murase, PhD
▪ Introduction
Dynamic contrast-enhanced CT (DCE-CT) acquires CT images serially after the administration of intravenous contrast agent. Recently, DCE-CT has become a major imaging technique and has been widely used for diagnosing normal tissue and benign and malignant tumors as well as for monitoring treatment effectiveness during and after therapy.1 In addition to its easy accessibility in most clinical facilities, DCE-CT can provide quantification of the hemodynamics of lesions, if combined with appropriate tracer kinetic analysis.2
One of the advantages of using CT for tracer kinetic analysis is that the relationship between the concentration of the administered iodinated contrast agent in the tissue and the attenuation of x-rays is almost always linear.2 This results in simpler analysis and fewer errors than dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI). On the other hand, the major disadvantages of using CT are its potentially high radiation exposure due to repetitive scanning and the need for iodinated contrast agent that can be nephrotoxic and allergenic.3 Recently, however, several studies have been performed to reduce these drawbacks in DCE-CT.4
In this chapter, the basic theory of tracer kinetic analysis and the practical methods for estimating kinetic parameters using DCE-CT will be described. The factors affecting the accuracy of the kinetic parameters obtained using DCE-CT and their correction methods will also be described.
▪ Relationship between CT Number and Concentration of Contrast Agent
Image contrast in CT is determined by differences in the attenuation of x-rays in different tissues. The CT number (in Hounsfield units) of tissues in the reconstructed images (CTt) is given by
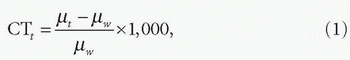
where µt and µw denote the linear attenuation coefficients of the tissue and water, respectively. After administration of contrast agent, the linear attenuation coefficient of the tissue at time t (µt(t)) is given by2
where µt(0) is the linear attenuation coefficient of the tissue immediately before administration of contrast agent and Δµt(t) is an increase of the linear attenuation coefficient at time t due to administration of contrast agent. Δµt(t) is related to the amount of the administered contrast agent and is directly proportional to the concentration of the contrast agent at time t (CCA(t)), thus yielding
where k is a constant of proportionality that depends on the energy spectrum of the x-ray beam passing through the tissue and the atomic constituents of the contrast agent.2 Since beam-hardening effects are usually corrected in most CT systems, it appears to be a good approximation that k does not vary among different tissues.2 Finally, an increase in CT number in tissue after administration of contrast agent (ΔCTt (t)) can be obtained from Eqs. (1), (2), and (3) as
where CTt(t) and CTt(0) denote the CT numbers in tissue at time t and before administration of contrast agent, respectively, and K = 1,000.k/µw. Therefore, the concentration of the administered contrast agent is proportional to an increase of CT number, that is, contrast enhancement.
In DCE-CT studies, the first time points of the concentration-time curves are generated and subtracted from the subsequent time points to ensure that the initial baseline concentration of the contrast agent is zero. After this normalization, the postcontrast density measurement using CT is directly proportional to the concentration of contrast agent, as given by Eq. (4). Since K in Eq. (4) is the same for the blood and tissues, the constant K cancels out in DCE-CT studies and thus does not need to be calculated or known.
▪ Basics of Tracer Kinetic Analysis
Vascular System
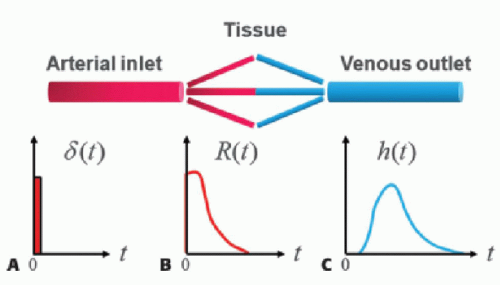
When a contrast agent is injected and enters a vascular system with a single inlet and a single outlet as a bolus as shown in Figure 4.1, the concentration-time curve measured at the exit of the vascular system is dispersed as the molecules in contrast agent may have different transit times through the system. Furthermore, there is a
delay time before they can be detected at the exit, because a specific time is necessary for traversing the system.
delay time before they can be detected at the exit, because a specific time is necessary for traversing the system.
Figure 4.1A shows an ideal bolus input at time 0. Mathematically, this is represented by Dirac delta function defined by
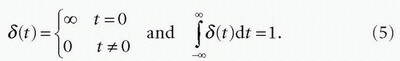
Figure 4.1B shows the corresponding tissue response function (R(t)), which shows the fraction of contrast agent remaining in the vascular system and is referred to as the “impulse residue (retention) function.” Figure 4.1C shows the distribution of transit times of contrast agent at the venous outlet through the vascular system, which is denoted by h(t) and is referred to as the “impulse response function.”
When we analyze the kinetic behavior of contrast agent in the vascular system (Fig. 4.1), a relationship between the inflow and outflow is based on the fundamental assumption that the system is both linear and stationary. This means that the response to an influx is assumed to be proportional to the injected dose and that the distribution of transit times through the system is constant in time.5
Concept of Convolution
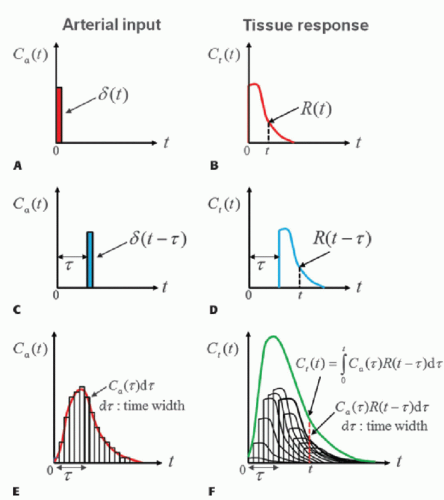
Mathematical solutions are represented for simple models under the condition of an ideal bolus, that is, the tracer appears for one capillary transit without recirculation. Actually, however, the input to the tissue is represented by a continuous concentration-time curve. In other words, the tissue response is a sum of the individual responses scaled in magnitude and shifted in time to match each bolus input, which is mathematically represented by convolution integral.
Figure 4.2 illustrates the concept of convolution integral. Figure 4.2A shows an ideal bolus input of contrast agent injected at time 0, that is, δ(t) defined by Eq. (5), and Figure 4.2B shows the corresponding impulse residue (retention) function (R(t)). Figure 4.2C shows an ideal bolus input injected at time t, that is, δ(t — τ), and Figure 4.2D shows the corresponding tissue response to this bolus input, which is represented by R(t — τ). When the arterial
input function (AIF) is not bolus (ideal) but continuous (real) as shown in Figure 4.2E, it can be interpreted as a series of bolus inputs with an area of Ca(τ)dτ (black square in Fig. 4.2E). In this case, the tissue response to the continuous input function can be interpreted as the sum of the responses to each bolus input given by Ca(τ)R(t-τ)dτ (Fig. 4.2F). Mathematically, this can be expressed as
input function (AIF) is not bolus (ideal) but continuous (real) as shown in Figure 4.2E, it can be interpreted as a series of bolus inputs with an area of Ca(τ)dτ (black square in Fig. 4.2E). In this case, the tissue response to the continuous input function can be interpreted as the sum of the responses to each bolus input given by Ca(τ)R(t-τ)dτ (Fig. 4.2F). Mathematically, this can be expressed as
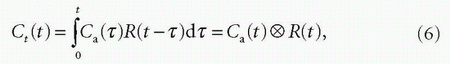
where the symbol ⊗ denotes convolution integral and τ is a dummy integration variable. When R(t) = 0 for t < 0, the following equation holds
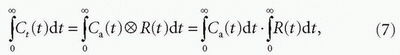
because the area of the convolution of two functions is equal to the product of the areas of the functions. If all tracers that enter the system leave it eventually, the principle of conservation of mass, that is, 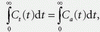 , holds (see Eq. (16)). Substituting this relation into Eq. (7) yields
, holds (see Eq. (16)). Substituting this relation into Eq. (7) yields
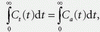 , holds (see Eq. (16)). Substituting this relation into Eq. (7) yields
, holds (see Eq. (16)). Substituting this relation into Eq. (7) yields
The idea of a system’s impulse response is commonly used in systems theory.6 When we consider a hypothetical tracer experiment with an ideal bolus input of tracer at the arterial inlet of the vascular system (Fig. 4.1A), the injected tracer would not appear all at once at the venous outlet6 and the transit times of tracer (contrast agent) through the vascular system are dispersed, as previously described. The distribution of transit times of tracer (contrast agent) at the venous outlet through the vascular system is described by the impulse response function (h(t)) (Fig. 4.1C). The relationship between h(t) and R(t) can be given by6

Differentiating Eq. (9) yields the alternative relation

Because h(t) is the probability density function of transit times of tracer through the vascular system, the first moment of h(t) gives the mean transit time (MTT) of the tracer, that is,


Fick Principle
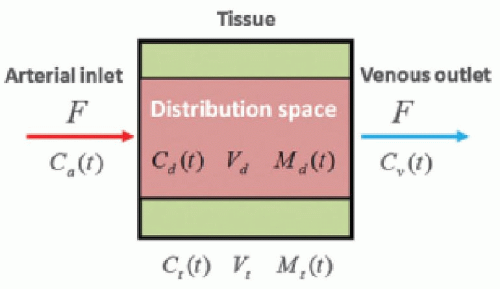
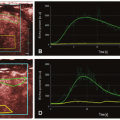
When a contrast agent is injected and enters a vascular system as shown in Figure 4.1, the concentration of contrast agent at the venous outlet of the system cannot be measured using DCE-CT, but only the average concentration within the distribution space of contrast agent in the tissue can be measured. Thus, we consider the vascular system consisting of the tissue region including the distribution space of contrast agent as illustrated in Figure 4.3. If the administered tracer enters and leaves the system with blood flow F as illustrated in Figure 4.3, then the temporal change of the tracer mass (concentration × volume) inside the tissue distribution space at time t is described by Fick principle as
where Cd(t), Ca(t), and Cv(t) are the concentrations of the tracer in the tissue distribution space, arterial blood, and venous blood at time t, respectively, and Md(t) is the mass of tracer inside the tissue distribution space with a volume of Vd, that is, Md(t) = Cd(t)Vd. If we use the concentration of contrast agent in whole blood (Cb(t)) for Ca(t), F represents whole blood flow. If the concentration of contrast agent in arterial plasma (Cp(t)) is used for Ca(t), F represents plasma flow and Cp(t) is given by Cp(t) = Cb(t)/(1 — Hct), where Hct denotes hematocrit.
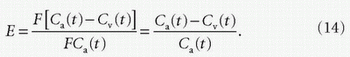
E is the fraction of the inflowing tracer that does not leave the system via outflow. Note that E is usually given in the form of E = (Ca(∝) — Cv(∝))/Ca(∝). The complement of E is also sometimes used, that is, T = 1 — E. Correspondingly, T is defined as the fraction of the inflowing tracer that leaves the system via outflow and is called the “throughput” or “transmission.”
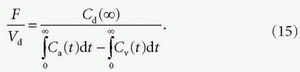
Equation (15) is known as “Kety-Schmidt equation.”7 When Cd(0) = 0 and Cd(∝) = 0, that is, all tracers entering the tissue leave it eventually, we obtain the following relation from Eq. (13):
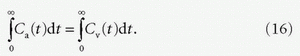
Equation (16) represents the principle of conservation of mass.
Central Volume Principle
The concentration of the tracer in venous blood (Cv(t)) in Eq. (13) can be given by convolution integral between Ca(t) and h(t) as Cv(t) = Ca(t) ⊗ h(t). Substituting this relation into Eq. (13) and integrating both sides of Eq. (13) yield2
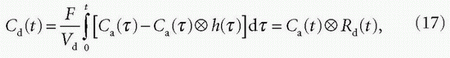
where
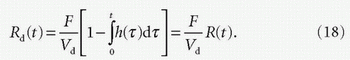
Rd(t) is referred to as the “tissue response function.” When we integrate both sides of Eq. (17) and use the principle of conservation of mass in a similar manner to that in Eq. (8), we obtain 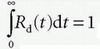 . Furthermore, integrating both sides of Eq. (18) and
. Furthermore, integrating both sides of Eq. (18) and
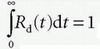 . Furthermore, integrating both sides of Eq. (18) and
. Furthermore, integrating both sides of Eq. (18) andusing this relation yield 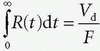 . Therefore, from Eq. (12), we obtain the MTT of tracer in the tissue distribution space (MTTd) as
. Therefore, from Eq. (12), we obtain the MTT of tracer in the tissue distribution space (MTTd) as
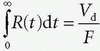 . Therefore, from Eq. (12), we obtain the MTT of tracer in the tissue distribution space (MTTd) as
. Therefore, from Eq. (12), we obtain the MTT of tracer in the tissue distribution space (MTTd) as
Equation (19) is the basic equation of “central volume principle,” stating that the MTT of tracer in the tissue distribution space can be given by the quotient of distribution volume and blood flow, and it is equal to the reciprocal of perfusion.
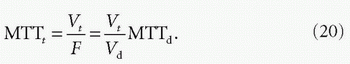
As illustrated in Figure 4.4, the following relation holds:
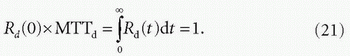
Thus, we obtain
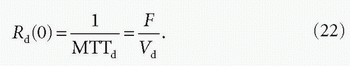
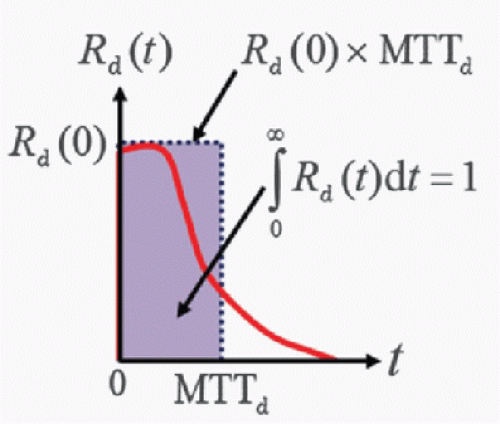 Figure 4-4. Relationship between the tissue response function (Rd(t)) and the MTT of tracer in the tissue distribution space (MTTd), from which the relation Rd(0) = 1/MTTd is obtained. |
Equation (22) implies that the initial height of the tissue response function is equal to F/Vd, that is, perfusion.
▪ Tracer Kinetic Analysis
Model-Independent Method and Model-Dependent Method
A tracer kinetic model is a mathematical description of the transport processes of the tracer within the tissue.6 Recently, various methods have been proposed for the quantification of kinetic parameters including perfusion.8,9 These methods can be roughly classified into two groups; one is a model-independent method and the other is a model-dependent method.
The model-independent method yields kinetic parameters for a tissue region described as a “black box” and thus does not provide insight into its internal structure.2 For quantification of perfusion using a model-independent method, deconvolution between the measured tissue residue curve and the AIF is needed to obtain the tissue response function, from which the perfusion can be quantified based on the central volume principle (Eq. (19)).10 Thus, the model-independent method is also called “deconvolution analysis.”
For a model-dependent method, compartment models are usually employed as tracer kinetic models, and kinetic parameters are quantified using compartment analysis based on the assumption that tissues can be kinetically represented by a set of interacting subcompartments that represent distinguishable states of an administered tracer.2
The kinetic models employed in compartment analysis can be classified as lumped parameter or distributed parameter models. The compartments are used to describe the physical distribution spaces of the tracer in the tissue. Conventionally, these compartments are assumed to be well mixed, that is, tracer movement is sufficiently fast and distributes evenly throughout the compartments, such that tracer concentration is only a function of time, but not space. Thus, conventional compartment models are called lumped parameter models. On the other hand, a distributed parameter model attempts to account for tracer concentration gradient within the compartments, such that concentration can be a function of both time and space.6
In contrast to the model-independent method, the modeldependent method generally requires specific knowledge about the vascular and compartmental architecture, the volumes of the compartments comprising the model, and the tracer-dependent permeability of compartment barriers. The assumptions in these models are generally valid under normal conditions, but for pathologic conditions, it is often difficult to independently verify which model parameters changed significantly, in particular when the model involves a large number of parameters or if the sensitivity ranges for the different parameters overlap significantly.11
Generally, model-independent deconvolution analysis has been applied to the data obtained by intravascular tracers.12 Recently, the accuracy of model-independent deconvolution analysis when applied to the data obtained by extravascular contrast agents, that is, the effect of the leakage of contrast agent from the intravascular space to the extravascular space, has been studied in Ref. 13
To investigate the effect of the leakage of contrast agent from the intravascular space to the extravascular space, it is necessary to use a model in which the concentration of contrast agent within the tissue is treated as a function of both time and position, that is, distributed parameter models.9 The distributed parameter models describe tracer concentration in the vascular compartment as a function of both time and position along the capillary and are generally believed to be more realistic than the lumped parameter models. One of the simple distributed parameter models is the tissue homogeneity model, which was initially developed by Johnson and Wilson.14 This model is based on both convective and diffusive transport of contrast agent in capillaries represented together as
a single cylinder and is composed of the intravascular space surrounded by the extravascular space. The two spaces are separated by a permeable barrier. St. Lawrence and Lee15 derived an approximate closed-form solution to the tissue homogeneity model using the adiabatic approximation. The details of the adiabatic approximation to the tissue homogeneity model will be described afterwards.
a single cylinder and is composed of the intravascular space surrounded by the extravascular space. The two spaces are separated by a permeable barrier. St. Lawrence and Lee15 derived an approximate closed-form solution to the tissue homogeneity model using the adiabatic approximation. The details of the adiabatic approximation to the tissue homogeneity model will be described afterwards.
Model-Independent Method
With a model-independent method, perfusion is quantified from the tissue response function obtained by deconvolution between the measured tissue concentration-time curve and the AIF.
The relationship between the concentration-time curve of contrast agent in tissue (Ct(t)) and that in a feeding artery, that is, the AIF (Ca(t)), can be described as convolution integral in a similar manner to Eq. (17):
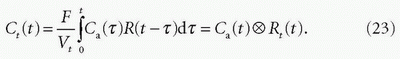
In Eq. (23), Rt(t) = FR(t)/Vt is the tissue response function, which is the amount of the contrast agent in the tissue in an idealized perfusion experiment, where a unit area bolus is instantaneously injected (R(0) = 1) and subsequently washed out by perfusion (R(∝) = 0). The procedure of finding a solution for the tissue response function that satisfies Eq. (23) is called “deconvolution analysis.” It is known from Eq. (22) that the initial height of the deconvolved tissue response function equals F/Vt, that is, perfusion.
Because the model-independent method only requires minimal user interaction or expertise in modeling, this approach appears to be easier to implement than the model-dependent method. Thus, the model-independent method has been applied to the quantification of perfusion in various organs such as the brain,16 the heart,17 and the lungs.18 Furthermore, this method has been applied to the evaluation of the hemodynamic change due to angiogenesis in tumors19 and monitoring the effect of therapeutic strategies on tumor vascular activity.20
Quantification of Perfusion Using Truncated Singular Value Decomposition
If it is assumed that the functions Ca(t) and R(t) in Eq. (23) are constant over small time intervals, Δt, Eq. (23) is reduced to
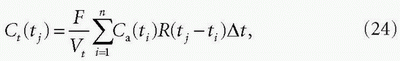
where ti and n denote the time of the ith frame and the total number of frames, respectively. It should be noted that it was assumed that t1 = 0 and the duration of each frame (Δt) is equal when converting Eq. (23) to Eq. (24). Equation (24) can then be formulated as a matrix equation
where 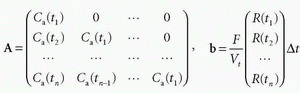 , and
, and 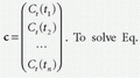 . To solve Eq. (25) for b is called “deconvolution,” which is an inverse problem and is a well-known ill-posed problem especially when there exists statistical noise. Thus, it is necessary to convert an ill-posed problem to a well-posed one to solve Eq. (25). The procedure of modifying an ill-posed problem to obtain a robust solution is called “regularization.” Of the regularization methods, the truncated singular value decomposition (TSVD) is a popular method for computing regularized solutions for ill-posed inverse problems.12,21
. To solve Eq. (25) for b is called “deconvolution,” which is an inverse problem and is a well-known ill-posed problem especially when there exists statistical noise. Thus, it is necessary to convert an ill-posed problem to a well-posed one to solve Eq. (25). The procedure of modifying an ill-posed problem to obtain a robust solution is called “regularization.” Of the regularization methods, the truncated singular value decomposition (TSVD) is a popular method for computing regularized solutions for ill-posed inverse problems.12,21
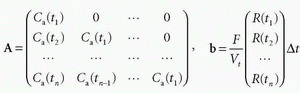 , and
, and 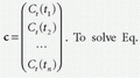 . To solve Eq. (25) for b is called “deconvolution,” which is an inverse problem and is a well-known ill-posed problem especially when there exists statistical noise. Thus, it is necessary to convert an ill-posed problem to a well-posed one to solve Eq. (25). The procedure of modifying an ill-posed problem to obtain a robust solution is called “regularization.” Of the regularization methods, the truncated singular value decomposition (TSVD) is a popular method for computing regularized solutions for ill-posed inverse problems.12,21
. To solve Eq. (25) for b is called “deconvolution,” which is an inverse problem and is a well-known ill-posed problem especially when there exists statistical noise. Thus, it is necessary to convert an ill-posed problem to a well-posed one to solve Eq. (25). The procedure of modifying an ill-posed problem to obtain a robust solution is called “regularization.” Of the regularization methods, the truncated singular value decomposition (TSVD) is a popular method for computing regularized solutions for ill-posed inverse problems.12,21With singular value decomposition, the matrix A in Eq. (25) can be expressed as the product of an n × n column orthogonal matrix U, an n × n diagonal matrix W, and the transpose of an n × n orthogonal matrix V,17 that is,
where wi (i = 1, 2,…, n) are the diagonal elements of W (singular values), which are nonnegative and can be ordered such that
The singular value decomposition constructs the matrices so that the inverse of A can be written as
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree