Dynamic Contrast-Enhanced T1-Weighted MR Imaging: Theory, Quantitative Aspects, and Practical Implementation
Henrik Bo Wiberg Larsson, MD, PhD
Thomas Fritz Hansen, MD
▪ Introduction
Dynamic contrast-enhanced T1-weighted MRI (DCE-MRI) is relative easy to integrate in a conventional MRI setup, it is cheap, and it has the potential to provide important physiologic parameters. Large interest has focused on determination of the leakage, also called the permeability, of the capillary membranes. The reason is that the permeability can be associated with changes in the vascular structure seen in malign transformed tissue and in tissue inflammation. The reason why the DCE-MRI has this potential is the size of the contrast agent (CA) molecules we are using. Typically, MRI CA agents are not freely diffusible in tissue, and the capillary membrane normally imposes restriction of diffusivity through the capillary membrane in normal tissue. In the brain, the normal blood-brain barrier (BBB) is nearly impermeable for conventional MRI CA, but the barrier breaks down in a number of diseases such as acute multiple sclerosis, inflammation, tumors, stroke, and possible dementia and epilepsy.1,2 Permeability is expressed as the permeability-surface area (PS) product, signifying that not only the permeability but also the available capillary surface area is determinant for the leakage. The PS product is ideally defined from a two-chamber experiment, the chamber having an initial concentration of C1 and C2 and J denoting the initial flux, that is, number of molecules moving from the first compartment to the second compartment per time unit. The relationship is
Note the transport is sign sensitive. The equation implies a first-order transport, that is, the flux out of a compartment is proportional to the concentration in that compartment, which is a reasonable assumption, because MRI CA are inert molecules and do not react with specific receptors. However, if the transport over the membrane is governed by a saturable transport system, the Michaelis-Menten kinetics is appropriate. This topic is outside the scope of this presentation. Using conventional MR CA, transport over the capillary membrane is driven by the concentration difference over the membrane as described by the equation. But this is not the whole story, because the blood flow through the capillary (the perfusion) will modify the actual flux over the membrane in a subtle way. Intuitively, the higher velocity of the blood through the capillary, the less likely is a passage over the capillary membrane. It turns out that the determining factor is the ratio PS/F, where F denotes the flow through the capillary. The dimension of the PS and F is mL/min or corresponding derivates. The relationship can be derived based on the following considerations: imaging a single capillary of length L and with radius R and having a specific PS product for the specific CA we are using. The flow is F, and the CA concentration at the inlet and outlet of the capillary is Cin and Co, respectively (see Fig. 8.1). In order to simplify matters, these concentrations are constant in time, and we assume that the extravascular concentration is so small that it can be ignored, which also means no return to the blood, once the CA molecules have left the blood over the membrane. These assumptions can easily be modified later if needed and will not change the basic principle we are aiming at. The loss of CA from a short-segment dx centered at position x along the capillary using Eq. (1) is
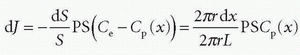
The CA change inside the capillary over this short segment where the concentrations in a thin layer at the entrance and exit of the short segment are C(x1) and C(x2), respectively, is
Combining and integrate these equations gives
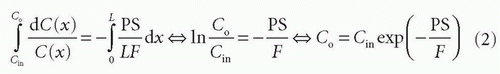
Thus, the concentration at the outlet becomes smaller when the PS product is large relative to F and vice versa, verifying our initial intuition. In the same setup, we can define the extraction fraction as the ratio of the amount taken up by the tissue per unit time to the total amount entering the tissue per unit time:
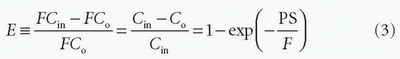
Renkin and Crone originally developed these equations.3,4 A freely diffusible CA for which PS/F is very large has an extraction of nearly one and is called a flow-limited tracer, because the amount
in tissue is determined by flow. If the CA is more or less confined to the vascular space, because it cannot easily diffuse over the capillary membrane, then PS/F is small and the extraction fraction approach zero. We then talk about a diffusion-limited CA, because the amount in the extravascular space is determined by the PS product. Note that the amount in the vascular space is of course determined by the delivery of the flowing blood entering the tissue. Because of the flow, Eq. (1) does not really describe the transport adequately. The transport is still linear meaning that the actual flux is proportional to the vascular concentration keeping F and PS the same. In order to deal with this situation, we define the clearance as the amount taken up by the tissue per unit time normalized to a reference concentration:
in tissue is determined by flow. If the CA is more or less confined to the vascular space, because it cannot easily diffuse over the capillary membrane, then PS/F is small and the extraction fraction approach zero. We then talk about a diffusion-limited CA, because the amount in the extravascular space is determined by the PS product. Note that the amount in the vascular space is of course determined by the delivery of the flowing blood entering the tissue. Because of the flow, Eq. (1) does not really describe the transport adequately. The transport is still linear meaning that the actual flux is proportional to the vascular concentration keeping F and PS the same. In order to deal with this situation, we define the clearance as the amount taken up by the tissue per unit time normalized to a reference concentration:
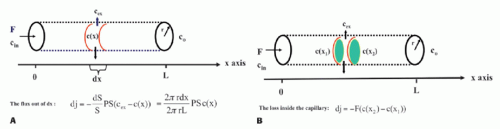 Figure 8-1. The single-unit capillary model used to derive the Crone and Renkin equation. Here, concentrations are only a function of position. Time dependence can be incorporated as well. |
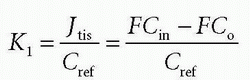
The dimension of the clearance is then volume per unit time. In words, the clearance is a (fictive) flow and is a measure of the volume of the reference solution containing the amount of the CA taken up or cleared by the tissue per unit time. Often, it is convenient to choose the reference concentration as the concentration of the CA at the inlet. In this case, we get
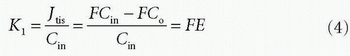
and Eq. (1) can be replaced with
In order not to deal with too many physiologic constants, the last equation is replaced with
using the argument of a membrane transport symmetry, although this may not be strictly correct. Note that K1 approach F for E going towards 1 for a free diffusible CA (i.e., a flow-limited CA or tracer), while K1 approaches the PS product for PS/F going towards zero (i.e., a diffusion-limited CA or tracer):
It is often convenient to normalize flux, PS product, F, and K1 to the tissue mass Mt or tissue volume Vt. In the following, relevant capital letters refer to no normalization, while small letters refer to a normalized metric, for example, F is in mL/min, while f is in mL blood/100 mL tissue/min. Strictly, this implies a dimension of f as 1/min, but it is important to keep the definition in mind. The choice between volume and mass is somewhat arbitrary, but strictly volume Vt and mass Mt are related as Mt = ρVt, where ρ is the tissue density, close to 1 g/mL.
DCE-MRI also allows determination of various compartment volumes, as the blood volume where Vp denotes the plasma volume, Vb denotes full blood volume, Ve denotes extravascular extracellular volume, and Vtis denotes extravascular intracellular tissue volume. Thus, Vb + Ve + Vtis = Vt, and Vb/Vt + Ve/Vt + Vtis/Vt = vb + ve + vtis = 1, where, for example, ve either is a fractional volume or has the dimension mL/100 mL or mL/100 g. The relationshipbetween Vb and Vp is given as Vp = Vb(1-Hctsv), where Hctsv is the small vessel hematocrit. More generally, in a given context, we talk about the volume of distribution (Vd) defined as Vd = Qt/Cref, where Qt is the number of CA molecules in a piece of tissue and Cref is the concentration of a reference solution of the CA, for example, plasma concentration. Ideally, Vd is defined in a situation where equilibration between a piece of tissue and the reference solution has been established. In words, Vd express the volume of the reference solution, which contains an amount equivalent to the amount in the tissue. If we normalize with the mass or volume of the tissue, we get the partition coefficient
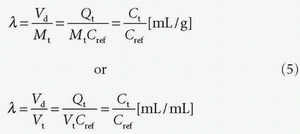
Note that the tissue concentration is then defined as Ct = Qt/Vt or Ct = Qt/Mt.
DCE-MRI can also be used for assessing tissue perfusion, for example, myocardial perfusion,5,6 and lately, it has been shown that when using a high scanner field strength of 3 T, brain perfusion can also be measured by DCE-MRI.7,8 Tissue perfusion is vital for normal functionality of the tissue, and lack of adequate tissue perfusion in various organs is the cause of many diseases, and probably more than 50% of all human deaths is directly coursed by lack of perfusion, creating tissue starvation, hypoxia, and infarction. In that perspective, it is remarkable that the methodology of perfusion measurement is still a very dynamic research area, and many perfusion methods are based on Kety’s pioneering work more than 60 years ago.9,10 All perfusion methods have advantages and disadvantages with regard to accuracy, precision, invasiveness, and expensiveness. Accuracy is not necessarily the ultimate goal, but the applicability in clinical decision making may be more relevant.
Tissue perfusion (f) is ideally defined as the volume of blood that enters a distinct part of the vascular system such as the capillaries in one unit of tissue mass (or volume) per unit time. The dimension is therefore mL blood/100 mL tissue/min, which is equal with 1/min. Often, the dimension mL blood/100 g tissue/min is used and reminisces earlier studies of perfusion based on in vitro studies, where perfusion was normalized to mass of tissue. Keeping the older terminology helps keeping the correct interpretation of perfusion, which may become blurred if using 1/min. Because 1 mL of tissue nearly has a mass of 1 g, the number is unchanged.
Determination of perfusion, permeability, and distribution volumes is based on a mathematical framework, the tracer kinetic theory, which in essence are equations describing the mass balance, keeping track of the transport of the CA as a function of time.
▪ Basic Tracer Kinetic Theory
The fundamental equation relating tissue concentration as a function of time, Ct(t), the arterial concentration as a function of time, Ca(t), perfusion f, and the residue impulse response function, RIF(t), is11
The residue impulse response function is defined as the CA fraction remaining in the tissue, after a brief injected bolus, in principle as a δ(t) function, directly into the tissue (or voxel), as a function of time. Thus, RIF is dimensionless, and because the entire bolus by definition is injection at time zero, the first function value will be one: RIF(0) = 1. If the entire bolus has a minimum transit time through the tissue (the voxel), of several seconds, then the RIF holds a function value of one until some of the CA molecules begin to leave the tissue in focus. From now on, the RIF will show a monotone decrease until it becomes zero: the entire bolus has left the tissue, or if it happens that a fraction becomes bound irreversible to the tissue, the RIF ends at a corresponding value, that is, the fraction that remains in the tissue infinitively; this value may be related to the extraction fraction (if back-diffusion does not occur). The assumption related to this equation is that the system is linear: Doubling the dose or concentration, Ca(t), results in a doubling of Ct(t) (f remains the same as well as the RIF), and a delayed input of “a” seconds, Ca(t — a), will result in a delayed output (Ct(t–a))and that the CA is not being produced or metabolized inside the tissue. Such a system is called a linear and time-invariant system. This is correct for many of the MRI CA we are using. However, one important additional point is that the CA has to be equally “visible” irrespective of the location of CA, be it in the plasma, the interstitial space, or intracellularly. Due to the fact that MRI CA acts by changing the longitudinal relaxation rate, R1, of adjacent water protons corresponding to the first hydration layer, the ability of water diffusion around the paramagnetic core of the CA can influence the level of visibility of the CA. As an example, if the CA becomes confined in a small compartment, without sufficient water exchange, then the CA loses its effect, because complete relaxation of the compartment is finite and therefore becomes invisible, that is, additional CA is without effect (see later).
Under these assumptions of linearity, ignoring the issue of water exchange, the convolution equation can be derived based on the following considerations. Imaging a short bolus Qin(0) = FCa(0) dt = Vtf Ca(0) dt enters a tissue volume (Vt) at time zero. Using the definition of the RIF, the tissue “response” is simply
If an additional input enters the tissue volume at a later time point, τ, the tissue response from this input is again
Note the time shift of τ seconds of the RIF to the right. The total tissue response is the sum of all tissue response functions. Generally, if we imagine that the entire arterial input function is composed of short inputs (δ-functions), entering as a continuous function of τ (substituting Δt with dτ), and the tissue response is linear in the input, the total tissue response at time t will be the sum of all the tissue impulse responses corresponding to each τ, and we get

Tissue concentration is here defined as the total amount of CA molecules per unit volume of tissue (or unit mass of tissue).
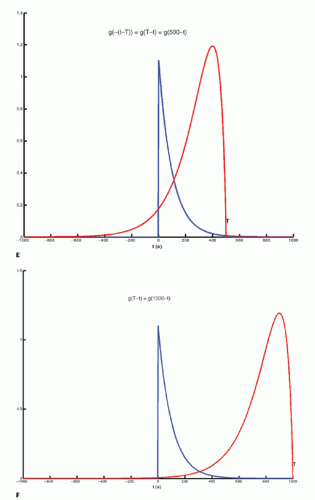
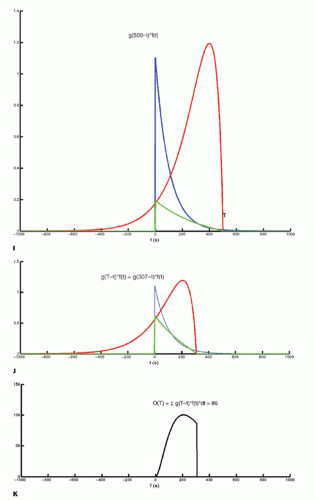
The integration of two functions as in Eq. (6) is called a convolution integral and is described from an operational point of view in Figure 8.2.
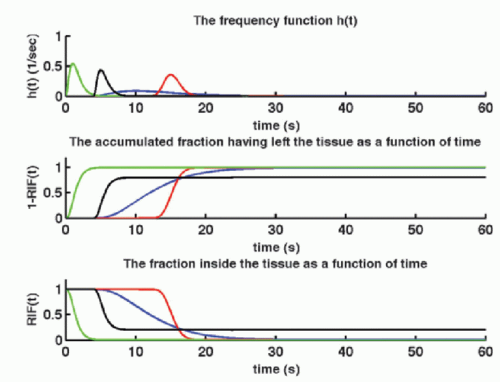
It is remarkable that Eq. (6), under the above-mentioned restriction, is always correct. Obviously, the goal is to find the perfusion f and the RIF(t). The physiologic interpretation of the RIF(t) is that this function describes the destiny of the contrast molecule inside the tissue. The RIF(t) is related to the distribution of transit times through the tissue: h(t). In words, h(t) is the fraction of the CA, which leaves the tissue at time t, per unit time, after a bolus injection:
where dN(t) is the number of CA molecules leaving the tissue at time t in the time interval dt and N0 is the entire bolus. Therefore, integrating over time in a time interval will give the fraction having left the tissue volume in that time interval, after a bolus injection. Specifically, in the time interval from zero (bolus injection) to time t1, the fraction having left the tissue is
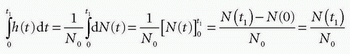
Note N(0) = 0: nothing has left the tissue at time zero. The fraction remaining in the tissue at time t1 is then
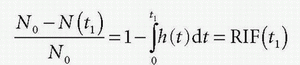
h(t) is similar to a probability density function, known from statistic, and the expectation value of the time weighted distribution is the typical transit time, the mean transit time MTT, and is given as
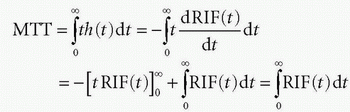
where we have used partial integration. Here, we assume that the RIF will be zero after sufficiently long time, that is, all CA molecules will leave the tissue eventually. Thus, MTT can be estimated either from the frequency function, h(t), or from the RIF(t). In Figure 8.3, h(t) is modeled as a gamma-variate function, and the corresponding RIF(t) and 1 — RIF(t) are also shown.
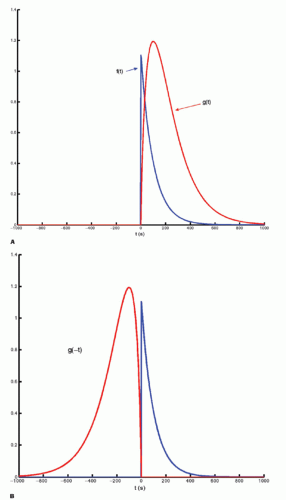 Figure 8-2. A: Convolution of two functions f(t) and g(t); the order of the functions is interchangeable. B: One of the functions is reflected by changing the sign of the argument, g(-t). |
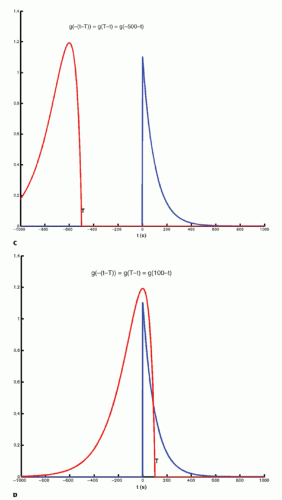 Figure 8-2. (Continued) C-F: The function g(T — t) is created; T determines the exact position of this function. |
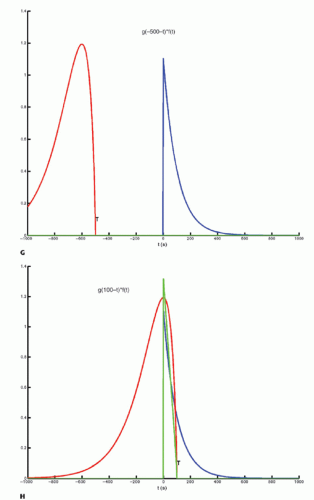 Figure 8-2. (Continued) G–I: For any given value of T, the function g(T — t) is multiplied with f(t) for all values of t, giving the green curve. |
Is the frequency function h(t) clinically interesting? In 1992, Kuschinsky and Paulson suggested that capillary perfusion heterogeneity had a significant impact on capillary diffusion capacity and that the capacity might be increased by homogenization of the perfusion pattern, a response elicited by neurovascular stimulation.12 This has lately been theoretically substantiated in relation to brain oxygen extraction.13 The variance of the frequency function, h(t), is a measure of this kind of capillary heterogeneity.
The partition coefficient λ was mentioned above, and if we use the arterial full blood concentration as a reference concentration, the partition coefficient becomes λ =Ct/Ca. We could also choose the capillary concentration in the middle of the capillary or the concentration at the outlet (in a vein): λ=Ct/Co. Ideally, the definition rests on an equilibrium experiment, but often one assumes instantaneous equilibration so λ =Ct(t)/Ca(t). Using the relation

the requirement of instantaneous equilibration can be relaxed. In the situation where the CA is confined to the vascular space, that is, no leakage, λ represents the blood volume, for example, in the brain, so λ becomes the cerebral blood volume, CBV. If the CA leaks easily through the capillary membrane, but does not enter the cells, then λ becomes the ve + vb. Finally, there exists an important relationship between MTT, λ, and f, called the central volume principle: MTT= λ/f.11 It can be obtained from our basic tracer kinetic equation using the Laplace transformation
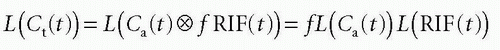
using the fact that Laplace transformation of a convolution integral equals the product of the Laplace transformed functions itself, and we also get from Eq. (7)
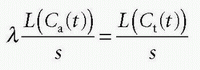
which inserted in the former equation gives
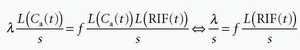
where we have eliminated L(Ca(t)) on each side of the equation. Taking the inverse Laplace transformation on each side of the last equation gives
Thus, the central volume principle is correct for any shape of RIF.
Above, we have alluded to the information embedded in the RIF. The question is how we can estimate RIF and f. Clearly, we need to sample many concurrent time points of Ca and Ct in order to estimate RIF and f. But we also need a model of the RIF(t), expressed as an analytical mathematical expression, containing our physiologic “free” parameters and which can be found in an optimization procedure.
▪ Estimation of RIF by Models
Building a model based on assumptions of the destiny of the CA in the tissue is intimately related to deriving an analytical expression for the RIF, as shown in the following.
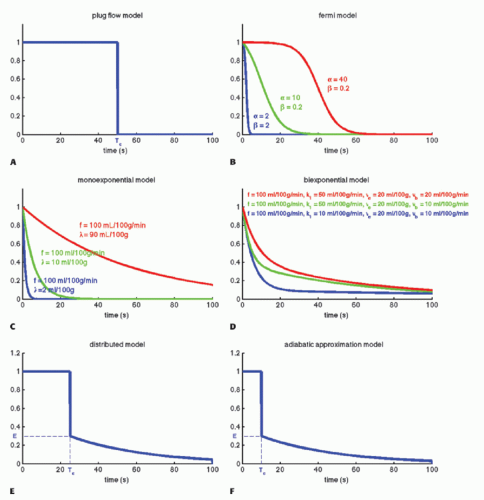
Imagine that we have some evidence that all tracer molecules entering as a bolus (ideally as a delta function) and traveling with the same speed (plug flow) through the tissue will leave the tissue (voxel) exactly at the same time Tc. Then, we would build a simple model of RIF as RIF(t) = 1 for 0 < t < Tc and RIF(t) = 0 for t > Tc. The RIF is shown in Figure 8.4A. If we inject a short bolus with concentration Ca(0) at time zero over a very short time interval Δt, then the tracer kinetic equation will look like
A unit step function, U(t), is defined as
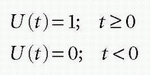
Then, the RIF(t) can conveniently be rewritten as
A more reasonable assumption is that we have a distribution of transit times where some tracer molecules are somewhat faster than others. The Fermi function may capture this situation, with the expression

having two adjustable parameters, where α determines the plateau (the minimal transit time) and β is related to the decay due to CA leaving the tissue. Note that if t = 0, RIF(0) = 1, and after the plateau, the function decays monotonously. The RIF(t) function is shown in Figure 8.4B.
A common approach is to consider the tissue as consisting of one or more compartments. Ideally, a compartment constitutes a volume fraction of the total tissue, where uniform concentration is established so fast at each time point so the concentration can be characterized as C(t), that is, the compartment is well mixed, and a possible slow diffusion within a compartment is ignored. The starting point for compartment analysis is based on an extension of the Fick principle
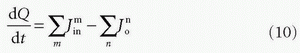
which states that the change in the amount of a CA in a given compartment is equal to the sum of all fluxes in and out of the compartment, where fluxes entering the compartment are positive and fluxes leaving the compartment are negative. As an example, we will derive the transport equation for a freely diffusible tracer. If membranes do not restrict diffusion through the tissue, the tissue (or voxel) will behave, as a one-compartment system, and the change of the amount in the tissue is according to the Fick principle14

assuming either one inlet and one outlet, or if multiple inlets exist, it will sum up to Jin and similar for the outlet. If blood is the source of delivery of the CA, and CA is not produced or metabolized inside the tissue and also leaves by blood plasma, then we have
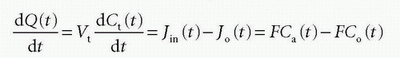
where Vt is the volume (or the mass) of the tissue, F is the total blood flow entering the tissue in focus (e.g., mL/min), and Ca(t) is the arterial concentration and Co(t) is the concentration at the outlet. For a freely diffusible CA, it is a reasonable assumption that a fast equilibrium exists between tissue concentration and concentration at the outlet at any time point, giving λ=Ct(t)/Co(t), that is, the partition coefficient. Depending on the particular CA used, λ can be larger, equal, or smaller than Vt. Inserting this relationship results in a solvable first-order differential equation:
With the initial conditions that Ct(0) = 0, the solutions is
This equation is appropriate for labeled water or radioactive xenon. Thus, the RIF is a simple monoexponential function (see Fig. 8.4C) with two physiologic constants, the perfusion and the partition coefficient. If the time course of the tissue concentration and the arterial concentration as a function of time are measured, then these two constants can easily be estimated using standard fitting procedures. This equation is based on the pioneering work of Kety.10
In the MR field, we are not so lucky as to have a freely diffusible CA yet. In, for example, muscle tissue, the extraction fraction during the first pass is around 50% to 60%; in the liver, it is probably higher; and in the brain, it is close to zero. For an MR CA, which is confined to the plasma volume, the equation will be
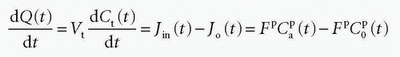
where Fp is the blood plasma flow entering the tissue in focus (e.g., mL/min), 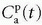 is the arterial plasma concentration, and
is the arterial plasma concentration, and 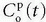 is the plasma concentration at the outlet. The conversion to full blood is given by
is the plasma concentration at the outlet. The conversion to full blood is given by
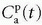 is the arterial plasma concentration, and
is the arterial plasma concentration, and 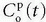 is the plasma concentration at the outlet. The conversion to full blood is given by
is the plasma concentration at the outlet. The conversion to full blood is given by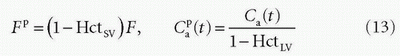
where HctSV and HctLV are the small-vessel hematocrit and largevessel hematocrit, respectively. The small-vessel hematocrit is used in conjunction with F because F relates to the microcirculation within the tissue, while the large-vessel hematocrit in conjunction with the input function relates to measurements in larger arteries. If we still can assume that 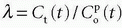 , we end up with a similar equation as Eq. (12):
, we end up with a similar equation as Eq. (12):
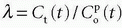 , we end up with a similar equation as Eq. (12):
, we end up with a similar equation as Eq. (12):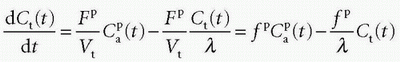
With the initial condition that Ct(0) = 0, the standard solution is
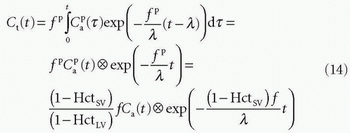
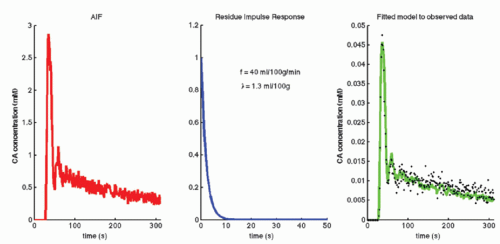
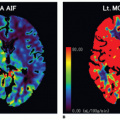
In fact, Eq. (14) has been used for brain perfusion with assumed intact BBB, and here, the MR CA behaves as an intravascular CA. Then, the partition coefficient λ is a measure of the cerebral blood volume, CBV. An example is shown in Figure 8.5. Whether one can use an intravascular CA for measurement of brain perfusion is controversial, because the results obtained are restricted by the assumption of the monoexponential RIF and may bias the results as pointed out by Lassen15 and Weisskoff et al.,16 and it is also uncertain which part of the vascular system is actually being measured. At least, it would be preferable to be able to model the RIF with a higher degree of freedom or without specifying an analytic model at all (see later).
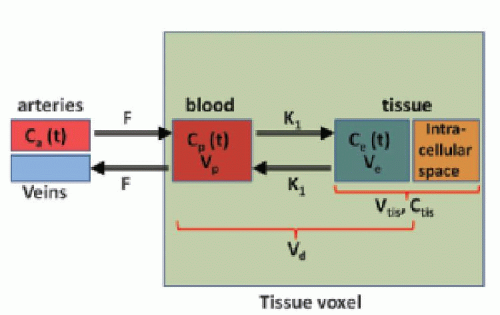
In many types of tissues, the extraction fraction is neither very low nor very high. In, for example, the heart muscle tissue, the extraction fraction during the first pass is around 50% to 60%, and the models above might not be the most appropriate in this situation. A two-compartment model is a better description of the transport of the CA. Here, we let these two compartments be represented by the blood plasma in tissue, Vp, with the CA plasma concentration Cp(t) in the tissue and the extravascular extracellular space in the tissue with volume Ve, with a CA concentration Ce(t) (see Fig. 8.6). Note the assumption of the blood volume being represented by just one concentration regardless of the location along the capillary. Using the Fick principle and assuming first-order diffusion between compartments, the transport equations for the two compartments are
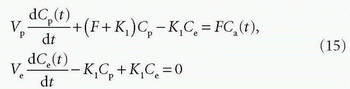
Here, F and K1 denote plasma perfusion and plasma clearance, respectively, and Ca(t) is arterial plasma concentration (we omit the superscript for graphical reasons). In addition, we have the following relationships:
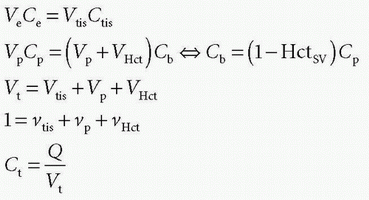
stating that the total tissue volume is composed of the extravascular tissue with volume, Vtis, the plasma volume, Vp, and the cell blood volume, VHct. It is assumed that the MR CA diffuses fast in the extravascular interstitial space. The second differential equation of Eq. (15) can be solved as done previously and gives
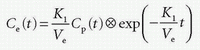
which inserted in the first differential equation gives
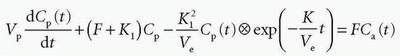
If we apply the Laplace transformation, then we can isolate L(Cp(t)) and L(Ce(t)), which we are searching for
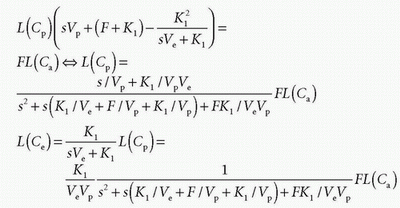
Using the Laplace transformation of exponentials as
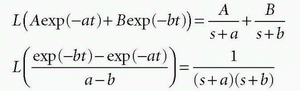
we can identify
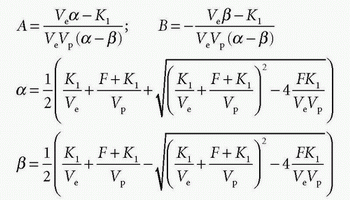
and Cp(t) and Ce(t) are then
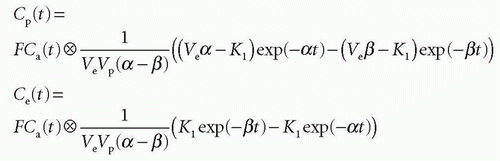
Total tissue concentration, Ct(t), is then found from
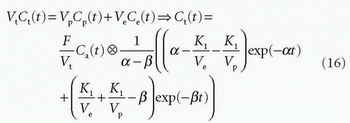
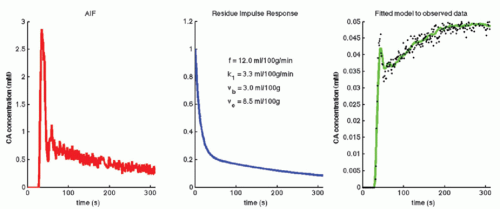
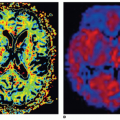
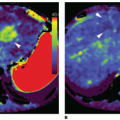
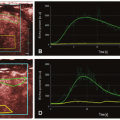
where f = F/Vt, and conveniently, all other constants are normalized by Vt. Conversion to full blood reference is also straightforward. Note that the residue impulse response function is biexponential and RIF(0) = 1 (see Fig. 8.4D). The two-compartment model has four free parameters: fp, 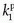 , ve, and vp. This type of model has previously been applied to a number of diseases in different organs including the brain lately.8,17 Brix already presented a simplified version of the two-compartment model in 1991.18 An example of using this model in a leaky brain tumor is shown in Figure 8.7.
, ve, and vp. This type of model has previously been applied to a number of diseases in different organs including the brain lately.8,17 Brix already presented a simplified version of the two-compartment model in 1991.18 An example of using this model in a leaky brain tumor is shown in Figure 8.7.
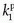 , ve, and vp. This type of model has previously been applied to a number of diseases in different organs including the brain lately.8,17 Brix already presented a simplified version of the two-compartment model in 1991.18 An example of using this model in a leaky brain tumor is shown in Figure 8.7.
, ve, and vp. This type of model has previously been applied to a number of diseases in different organs including the brain lately.8,17 Brix already presented a simplified version of the two-compartment model in 1991.18 An example of using this model in a leaky brain tumor is shown in Figure 8.7.The first tracer kinetic model, often called the Tofts model, used in conjunction with MRI, focused on estimation of BBB permeability of multiple sclerosis plaques and brain tumors19,20:
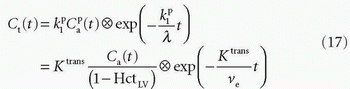
Note that 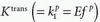 is the tissue clearance (tissue uptake transfer constant) with reference to plasma with the dimension mL plasma cleared/100 mL tissue/min (a capital letter in Ktrans is traditional used),
is the tissue clearance (tissue uptake transfer constant) with reference to plasma with the dimension mL plasma cleared/100 mL tissue/min (a capital letter in Ktrans is traditional used), 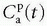 is plasma concentration of the CA, while Ca(t) is full blood concentration. The assumptions behind this model are, firstly, that the vascular volume fraction in the tissue is vanishing small and can be ignored and, secondly, that the arterial plasma concentration of the CA represents the input function to a distribution volume, which is equivalent with the extravascular extracellular space, ve. Note that if ps » f (E=1), then Ktrans = fp, and we are back to Eq. (12). If ps « f (E → 0), Ktrans = ps. Thus, the residue impulse response function in this case is RIF(t) = exp(-Ktranst/ve). After the introduction of Eq. (17), it was quickly being used outside the brain, and it soon became clear that the vascular component could not be ignored and constituted a significant part of the MR signal in many types of tissue, for example, in the heart.21 In order to ameliorate this situation, the vascular volume was included giving the following equation, often denoted as the extended Tofts model22:
is plasma concentration of the CA, while Ca(t) is full blood concentration. The assumptions behind this model are, firstly, that the vascular volume fraction in the tissue is vanishing small and can be ignored and, secondly, that the arterial plasma concentration of the CA represents the input function to a distribution volume, which is equivalent with the extravascular extracellular space, ve. Note that if ps » f (E=1), then Ktrans = fp, and we are back to Eq. (12). If ps « f (E → 0), Ktrans = ps. Thus, the residue impulse response function in this case is RIF(t) = exp(-Ktranst/ve). After the introduction of Eq. (17), it was quickly being used outside the brain, and it soon became clear that the vascular component could not be ignored and constituted a significant part of the MR signal in many types of tissue, for example, in the heart.21 In order to ameliorate this situation, the vascular volume was included giving the following equation, often denoted as the extended Tofts model22:
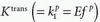 is the tissue clearance (tissue uptake transfer constant) with reference to plasma with the dimension mL plasma cleared/100 mL tissue/min (a capital letter in Ktrans is traditional used),
is the tissue clearance (tissue uptake transfer constant) with reference to plasma with the dimension mL plasma cleared/100 mL tissue/min (a capital letter in Ktrans is traditional used), 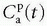 is plasma concentration of the CA, while Ca(t) is full blood concentration. The assumptions behind this model are, firstly, that the vascular volume fraction in the tissue is vanishing small and can be ignored and, secondly, that the arterial plasma concentration of the CA represents the input function to a distribution volume, which is equivalent with the extravascular extracellular space, ve. Note that if ps » f (E=1), then Ktrans = fp, and we are back to Eq. (12). If ps « f (E → 0), Ktrans = ps. Thus, the residue impulse response function in this case is RIF(t) = exp(-Ktranst/ve). After the introduction of Eq. (17), it was quickly being used outside the brain, and it soon became clear that the vascular component could not be ignored and constituted a significant part of the MR signal in many types of tissue, for example, in the heart.21 In order to ameliorate this situation, the vascular volume was included giving the following equation, often denoted as the extended Tofts model22:
is plasma concentration of the CA, while Ca(t) is full blood concentration. The assumptions behind this model are, firstly, that the vascular volume fraction in the tissue is vanishing small and can be ignored and, secondly, that the arterial plasma concentration of the CA represents the input function to a distribution volume, which is equivalent with the extravascular extracellular space, ve. Note that if ps » f (E=1), then Ktrans = fp, and we are back to Eq. (12). If ps « f (E → 0), Ktrans = ps. Thus, the residue impulse response function in this case is RIF(t) = exp(-Ktranst/ve). After the introduction of Eq. (17), it was quickly being used outside the brain, and it soon became clear that the vascular component could not be ignored and constituted a significant part of the MR signal in many types of tissue, for example, in the heart.21 In order to ameliorate this situation, the vascular volume was included giving the following equation, often denoted as the extended Tofts model22: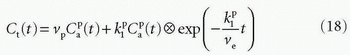
The specific assumption associated with this expression is that the plasma fraction in the tissue has a CA concentration equal with the arterial plasma concentration (which is measured), and the loss from the vascular space due to leakage is so small that it can be ignored; obviously, this equation implicitly suggests a very small 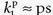 product. The extended Tofts model has three unknown free parameters:
product. The extended Tofts model has three unknown free parameters: 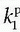 , ve, and vp. Formally, the RIF(t) = vpδ(t) + exp(-Ktranst/ve).
, ve, and vp. Formally, the RIF(t) = vpδ(t) + exp(-Ktranst/ve).
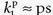 product. The extended Tofts model has three unknown free parameters:
product. The extended Tofts model has three unknown free parameters: 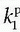 , ve, and vp. Formally, the RIF(t) = vpδ(t) + exp(-Ktranst/ve).
, ve, and vp. Formally, the RIF(t) = vpδ(t) + exp(-Ktranst/ve).It is increasingly being recognized that Eq. (18) in some situation is inadequate to describe the CA transport in some type of tissues, or at least, the interpretation of 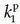 is somewhat ambiguous, as it is often correlated with both perfusion and permeability.23,24 and 25 It has even been shown that a good fit of Eq. (18) to data is no guaranty of obtaining accurate results,24 and more elaborate methods should probably be used (see below).
is somewhat ambiguous, as it is often correlated with both perfusion and permeability.23,24 and 25 It has even been shown that a good fit of Eq. (18) to data is no guaranty of obtaining accurate results,24 and more elaborate methods should probably be used (see below).
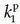 is somewhat ambiguous, as it is often correlated with both perfusion and permeability.23,24 and 25 It has even been shown that a good fit of Eq. (18) to data is no guaranty of obtaining accurate results,24 and more elaborate methods should probably be used (see below).
is somewhat ambiguous, as it is often correlated with both perfusion and permeability.23,24 and 25 It has even been shown that a good fit of Eq. (18) to data is no guaranty of obtaining accurate results,24 and more elaborate methods should probably be used (see below).Equation (18) is a good starting point for deriving the famous Patlak equation.26 If leakage is unidirectional, that is, negligible backflux, then RIF(t) = 1, and Eq. (18) becomes
Again, the assumptions are a unidirectional transport, that is, an irreversible leakage, and the arterial plasma with concentration
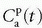 serves as a source for the leakage inside the tissue, and importantly, the CA loss from this vascular space is so small that it can be ignored. Obviously, for an inert typical MR CA agent,
serves as a source for the leakage inside the tissue, and importantly, the CA loss from this vascular space is so small that it can be ignored. Obviously, for an inert typical MR CA agent, 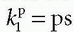 product. Dividing both sides of the equation with the instantaneous
product. Dividing both sides of the equation with the instantaneous 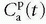 results in the Patlak equation
results in the Patlak equation
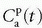 serves as a source for the leakage inside the tissue, and importantly, the CA loss from this vascular space is so small that it can be ignored. Obviously, for an inert typical MR CA agent,
serves as a source for the leakage inside the tissue, and importantly, the CA loss from this vascular space is so small that it can be ignored. Obviously, for an inert typical MR CA agent, 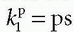 product. Dividing both sides of the equation with the instantaneous
product. Dividing both sides of the equation with the instantaneous 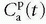 results in the Patlak equation
results in the Patlak equation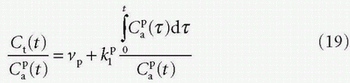
If one then plots the ratio 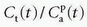 as a function of
as a function of 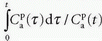 , one will get at straight line with the slope
, one will get at straight line with the slope 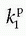 and an intercept of vp, which are the two unknown in this equation. As pointed out by Patlak, vp in reality includes the steady-state volume of distribution of all reversible compartments. The Patlak analysis has been used successfully in many nuclear medicine studies and seems also useful when measuring the BBB permeability in the brain when using DCE-MRI.17,27 However, it is important to restrict its use in accordance with the assumptions. When used, one will notice an initial phase in the Patlak plot, which is related to a vascular transition, and the Patlak equation only relates to the slowly steady increase afterwards (see Fig. 8.8). In order to understand the entire curve obtained, it is more instructive to start with the two-compartment model, eliminating all terms related to the backdiffusion, which we now assume can be neglected:
and an intercept of vp, which are the two unknown in this equation. As pointed out by Patlak, vp in reality includes the steady-state volume of distribution of all reversible compartments. The Patlak analysis has been used successfully in many nuclear medicine studies and seems also useful when measuring the BBB permeability in the brain when using DCE-MRI.17,27 However, it is important to restrict its use in accordance with the assumptions. When used, one will notice an initial phase in the Patlak plot, which is related to a vascular transition, and the Patlak equation only relates to the slowly steady increase afterwards (see Fig. 8.8). In order to understand the entire curve obtained, it is more instructive to start with the two-compartment model, eliminating all terms related to the backdiffusion, which we now assume can be neglected:
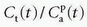 as a function of
as a function of 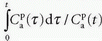 , one will get at straight line with the slope
, one will get at straight line with the slope 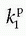 and an intercept of vp, which are the two unknown in this equation. As pointed out by Patlak, vp in reality includes the steady-state volume of distribution of all reversible compartments. The Patlak analysis has been used successfully in many nuclear medicine studies and seems also useful when measuring the BBB permeability in the brain when using DCE-MRI.17,27 However, it is important to restrict its use in accordance with the assumptions. When used, one will notice an initial phase in the Patlak plot, which is related to a vascular transition, and the Patlak equation only relates to the slowly steady increase afterwards (see Fig. 8.8). In order to understand the entire curve obtained, it is more instructive to start with the two-compartment model, eliminating all terms related to the backdiffusion, which we now assume can be neglected:
and an intercept of vp, which are the two unknown in this equation. As pointed out by Patlak, vp in reality includes the steady-state volume of distribution of all reversible compartments. The Patlak analysis has been used successfully in many nuclear medicine studies and seems also useful when measuring the BBB permeability in the brain when using DCE-MRI.17,27 However, it is important to restrict its use in accordance with the assumptions. When used, one will notice an initial phase in the Patlak plot, which is related to a vascular transition, and the Patlak equation only relates to the slowly steady increase afterwards (see Fig. 8.8). In order to understand the entire curve obtained, it is more instructive to start with the two-compartment model, eliminating all terms related to the backdiffusion, which we now assume can be neglected:Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree