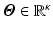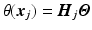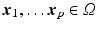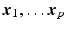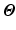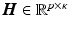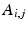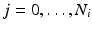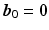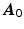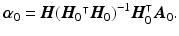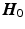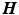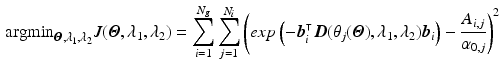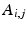Fibers Estimation from Arbitrarily Spaced Diffusion Weighted MRI
Fig. 1.
Circumferential and long-axis coordinate system.
We assume the helix angle distribution is given by a set of degrees-of-freedom
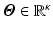
(DOF), such that the following linear relation holds:
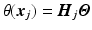
,
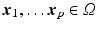
, with
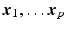
the set of discrete mesh points. Each element of
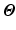
is associated to one vertex of the surface “patchs” depicted in Fig.
2(a)–(b). Hence, the operator
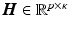
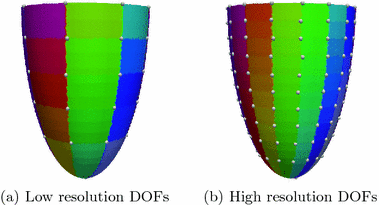
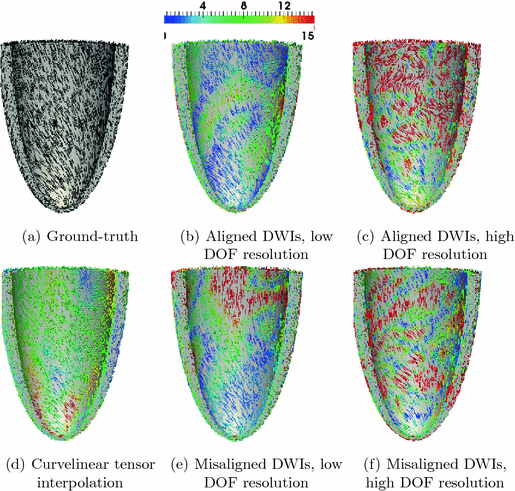
summarizes the linear interpolations from the patchs-corners to the rest of the surface, and then from the surfaces to the heart’s volume using Poisson interpolation. Two sets of degree of freedom were used in the numerical examples, a low resolution set with 82-DOFs (Fig.
2(a)) and a high-resolution set with 322 DOFs (Fig.
2(b)). We assume that we have a set of measured diffusion weighted signal values
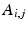
, for
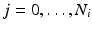
voxels for each diffusion encoding direction
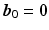
,
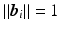
,
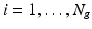
. The fiber estimation method consists then of the following steps:
Step1: Being
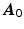
the values of the zero-weighted images at the measured voxels, we first reconstruct these values in the whole heart domain as
The linear operator
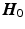
consists of the rows of
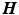
, which maps the DOFs to the zero-weighted slices.
Step2: We then minimize the functional
Note that since we directly compare the mismatch in the graduation itself, each voxel and diffusion gradient are equally weighted in the functional.
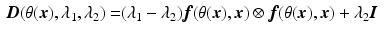
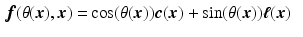
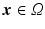 , with
, with 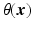 the helix angle of the fiber and
the helix angle of the fiber and 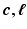 the local circumferential and long-axial directions, respectively (see Fig. 1(a)–(b)). The values
the local circumferential and long-axial directions, respectively (see Fig. 1(a)–(b)). The values